Метрические задачи. определение расстояний и углов. определение натурального вида

ПЛОСКОЙ ФИГУРЫ

Задача № 5.1. Определить длину отрезка АВ.

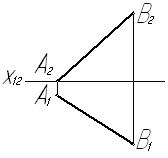
Рис. 25

Если отрезок параллелен плоскости проекций, то его длина определяется длиной проекции отрезка на этой плоскости. Поэтому для решения задачи построим дополнительную ортогональную проекцию отрезка на плоскости, параллельной этому отрезку или проходящей через него и перпендикулярной к одной из плоскостей проекций.

Строим дополнительную ортогональную проекцию А₄В₄ отрезка АВ на плоскости П₄ проходящей через отрезок и перпендикулярной к плоскости П₁. Ось Х₁₄ совпадает с горизонтальной проекцией А₁В₁ отрезка АВ. Ось Х₁₂ проведена через фронтальную проекцию А₂ точки А. Расстояние от оси Х₁₄ до дополнительных проекций А₄ и В₄ точек А и В равно расстоянию от фронтальных проекций точек А₂ и В₂ этих точек до оси Х₁₂. Длина дополнительной ортогональной проекции А₄В₄ отрезка АВ на плоскости проекций П₄ равна длине отрезка АВ

Задача № 5.2. Определить расстояние от точки А до прямой l.

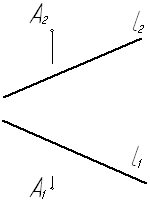
Рис. 26

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую.

На эпюре проекции перпендикуляра к прямой можно построить, если прямая параллельна плоскости проекций. Поэтому сначала строим дополнительную ортогональную проекцию прямой l и точки А на плоскости проекций П₄, параллельной прямой l и перпендикулярной к плоскости П₁. При этом ось Х₁₄ параллельна l₁. Для построения дополнительной проекции прямой l на ней отмечены точки 1 и 2. Проводим дополнительную проекцию А₄К₄ перпендикуляра (А₄К₄ ^l₄),а затем строим горизонтальную проекцию перпендикуляра А₁К₁ и его фронтальную проекцию А₂К₂. По двум проекциям отрезка АК(А₁К₁ и А₂К₂) находим его длину путём поворота вокруг фронтально проецирующей оси i, проходящей через точку А, до положения параллельного плоскости П₁. Длина отрезка А₁К¢₁ и есть расстояние от точки А до прямой l.

Задача № 5.3. Определить расстояние от точки А до плоскости a(h Çf).

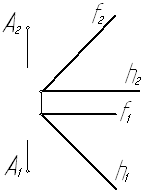
Рис. 27

Расстоянием от точки до плоскости является длина отрезка перпендикуляра, опущенного из точки на плоскость.

Из точки А проведём перпендикуляр n к плоскости a(h Çf) - (n₂ ^ f₂, n₁ ^ h₁) и построим точку К, в которой перпендикуляр n пересекает плоскость a. Построение выполняется с помощью прямой t, лежащей с перпендикуляром n в одной фронтально проецирующей плоскости.

Длина отрезка перпендикуляра АК определяется аналогично длине отрезка АВ в задаче № 5.1, основная ось Х₁₂ проведена через точку К₂, а дополнительная ось Х₁₄ совпадает с n_1. Полученный отрезок А₄К₄ на плоскости П₄ измеряет расстояние от точки А до плоскости a.

Задача № 5.4. Определить расстояние между скрещивающимися прямыми l и m, l ^ П₁ и m - прямая общего положения.

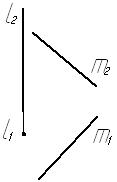
Рис. 28

Под расстоянием между скрещивающимися прямыми понимается длина отрезка перпендикуляра, общего для обеих прямых.

Если одна из скрещивающихся прямых lперпендикулярна к плоскости проекций П₁, то их общий перпендикуляр АВ параллелен плоскости проекций П₁. При этом прямой угол между перпендикуляром и прямой m проецируется на плоскости П₁ в прямой угол, и проекция отрезка перпендикуляра А₁В₁ между прямыми l и m определяет расстояние между ними.

Задача № 5.5. Определить расстояние между скрещивающимися прямыми h и f; h ççП₁ и f ççП₂

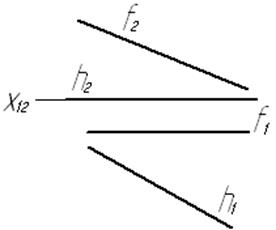
Рис. 29

Обе прямые h и f занимают положение линий уровня. Для перехода к задаче № 5.4 вводим дополнительную плоскость проекций П₄ ^ П₁ и П₄ ^ h, ось Х₁₄ перпендикулярна к h₁. Длина проекции А₄В₄ отрезка АВ общего перпендикуляра прямых h и f равна искомому расстоянию, так как отрезок АВ параллелен плоскости проекций П_4..