Обыкновенные дифференциальные уравнения

Основные понятия теории обыкновенных дифференциальных уравнений. Задача Коши. Теорема существования и единственности решения. Составление дифференциального уравнения первого порядка. Модели экономической динамики.

Дифференциальные уравнения первого порядка. Методы интегрирования дифференциальных уравнений первого порядка. Линейные дифференциальные уравнения первого порядка.

Линейные дифференциальные уравнения высших порядков. Однородные и неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью. Метод Лагранжа вариации произвольной постоянной. Системы линейных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Ряды

Понятие числового ряда. Сходимость числового ряда. Простейшие свойства сходящихся рядов. Необходимое условие сходимости числового ряда. Признаки сходимости рядов с положительными членами. Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.

Функциональные ряды. Степенные ряды. Теорема Абеля. Область и интервал сходимости степенного ряда. Ряды Тейлора и Маклорена. Разложение элементарных функций в степенные ряды. Применение рядов к приближенным вычислениям.

Ряды Фурье. Разложение функций в ряды Фурье.

Раздел I. ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ

Аналитическая геометрия на плоскости

Метод координат

Одна из главных особенностей метода аналитической геометрии заключается в употреблении чисел для определения положения геометрических образов. Числа, определяющие положение геометрических образов, называются их координатами.

Прямоугольной декартовой системой координат на плоскости называют совокупность трех условий:

1) две взаимно перпендикулярные прямые: ось x, или ось абсцисс, и ось y, или ось ординат;

2) начало координат – точка пересечения осей; положительное направление на каждой из осей;

3) единица масштаба на обеих осях одна и та же.

Положение точки М относительно выбранной системы координат определяется двумя координатами: абсциссой x, которая равна расстоянию от точки М до оси ординат, взятому со знаком «плюс» или «минус» в зависимости от того, находится ли точка М вправо или влево от нее; ординатой y, которая определяется как расстояние от точки М до оси абсцисс, взятому со знаком «плюс» или «минус», смотря по тому, находится ли точка сверху или снизу от оси абсцисс (рисунок 1).

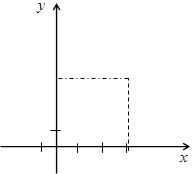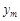
M

1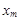

0 1

Рисунок 1

Таким образом, каждой точке плоскости соответствует упорядоченный набор двух действительных чисел и наоборот.

Обозначение: М(x; y).

Оси координат делят всю плоскость на четыре квадранта (рисунок 2).

IV

III

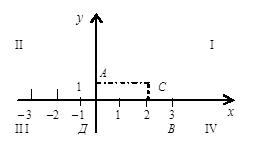
Рисунок 2

Пример 1. Точки имеют следующие координаты: А(0; 2), B(3; 0), C(2; 1), Д(–3; –1), O(0; 0).

Расстояние между двумя точками А(х_А; у_А) и В(х_В; у_В) вычисляется по формуле

=

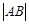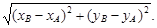
Пример 2. Длина отрезка АВ, где А(2; –1), B(3; 5), равна

= = =

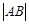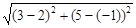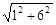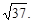
Пусть точка С лежит на отрезке АВ и делит его в отношении
λ = 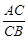. Если А(х_А; у_А), В(х_В; у_В), то координаты точки С(х_С; у_С) определяются следующими формулами:

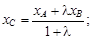
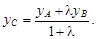
В частности, координаты середины отрезка АВ (т. е. при λ = 1) находятся по формулам

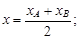
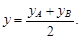
Пример 3. Отрезок АВ, где А(7; –2), B(–1; 3), разделен на три равные части. Найти координаты точек деления (рисунок 3).

A C D B

Рисунок 3

Решение

Точка С делит отрезок АВ в отношении 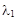= = 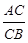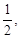поэтому

=

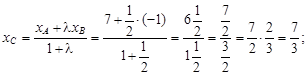
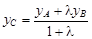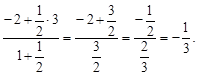
Таким образом, С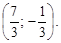

Точка D делит отрезок АВ в отношении 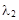= = 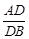= 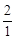2. Тогда

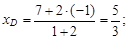
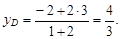
Таким образом, D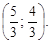

Тест 1. Координаты середины отрезка АВ, где А(0; 4), B(–3; –2):

1)

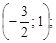
2)

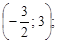
3) (–3; 2);

4) (4; –5).

Тест 2. Длина отрезка АВ, где А(0; 4), B(–3; –2):

1)

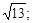
2) 3;

3)

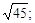
4) 4.

Ответы на тестовые задания

Номер теста
Правильный ответ

Прямая линия

Всякое уравнение первой степени относительно декартовых координат изображает прямую линию и, обратно, всякая прямая линия изображается в декартовых координатах уравнением первой степени.

Уравнение прямой по угловому коэффициенту k = tg j, где угол, образованный прямой с положительным направлением оси абсцисс, и величине отрезка b, отсекаемого данной прямой на оси ординат, считая от начала координат, имеет вид y = kx + b.

Если φ = 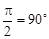, то tg φ = tg 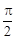не существует. Поэтому уравнение примет вид x = a.

Пример 4. В уравнении y = 3x – 2 угловой коэффициент k = 3,
b = –2, (x; y) − координаты любой точки прямой.

Пусть x = 1, тогда y = 3 × 1 – 2 = 1. Значит, точка (1; 1) принадлежит прямой.

Точка (2; –5) не принадлежит прямой, так как ее координаты не удовлетворяют уравнению, т. е. –5 ≠ 3 × 2 – 2; –5 ≠ 4.

Тест 3. Прямой y = –2x + 1 принадлежит точка:

1) (0; 3);

2) (–1; 3);

3) (2; 3);

4) (–2; 1).

Тест 4. Прямая y = –2x + 5 образует с положительным направлением оси ОX угол α, равный:

1) –2;

2) tg(–2);

3) arctg(–2);

4) arctg 5.

Условие параллельности двух прямых: k₁ = k₂.

Условие перпендикулярности двух прямых: k₁ × k₂ = –1 или .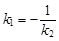

Пример 5. Прямые y = 2x – 3 и y = 2x + 5 параллельны, так как
k₁ = 2 = k₂. Прямые y = 3x + 5 и y = 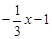перпендикулярны, так как
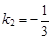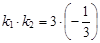k₁ = 3, и = –1.

Тест 5. Угловой коэффициент и отрезок, отсекаемый на оси ординат прямой 2x – y + 3 = 0, равны:

1) k = –1; b = 2;

2) k = 3; b = 2;

3) k = 2; b = 3;

4) k = 2; b = –1.

Тест 6.Уравнение прямой, проходящей через начало координат и наклонной к оси ОX под углом 45°, имеет вид:

1) y = x;

2) y = x + 45;

3) y = 45x;

4) y =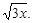

Тест 7. Уравнение прямой, параллельной прямой y = 4x – 3 и проходящей через начало координат, имеет вид:

1) y = 3x + 4;

2) y = 4x;

3) y = 3x;

4) y =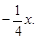

Тест 8. Уравнение прямой, перпендикулярной прямой y = 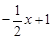и проходящей через начало координат, имеет вид:

1) y = 2x;

2) y = x – ;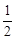

3) y = –2x + 1;

4) y = –2x.

Уравнение прямой, проходящей через точку (х₀; у₀) и имеющей угловой коэффициент k, имеет вид y – y₀ = k(x – x₀).

Пример 6. Написать уравнение прямой, которая проходит через точку А(3; –1) и параллельна оси абсцисс.

Решение

Так как прямая проходит через точку A(3; –1), то ее уравнение имеет вид y – (–1) = k(x – 3). Поскольку прямая параллельна оси абсцисс ОX, то угол между прямой и осью ОX равен 0°, а значит k = tg 0° = 0. Следовательно, y + 1 = 0 × (x – 3) или y + 1 = 0.

Тест 9. Уравнение прямой, проходящей через точку А(–5; –1) и параллельной прямой y = 3x + 7, имеет вид:

1) y + 1 = 3(x + 5);

2) y + 5 = 3(x + 1);

3) y – 1 = 3(x + 5).

Угол между φи прямыми y = 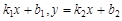вычисляется по формуле

tg φ =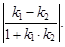

Тест 10. Угол между прямыми y = 2x + 1, y = –5x + 3 определяется по формуле:

1) tg φ =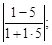

2) tg φ =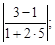

3) tg φ=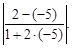

Прямая, проходящая через две данные точки А(х₁; у₁) и В(х₂; у₂), определяется уравнением

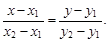
Пример 7.Записать уравнение прямой, проходящей через точки
А(3; –1), B(5; 0).

Решение

Воспользуемся уравнением прямой, проходящей через две точки.

Получим 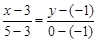или .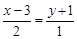

Так как последнее равенство представляет собой пропорцию, то по свойству пропорции (x – 3) × 1 = (y + 1) × 2.

После преобразований получим x – 3 = 2y + 1, или x – 3 – 1 = 2y, или x – 4 = 2y.

Окончательно, y =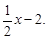

Тест 11. Уравнение стороны АВ треугольника АВС, у которого вершины имеют координаты А(1; –2), B(–3; –7), C(–1; –4), имеет вид:

1)

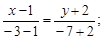
2)

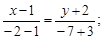
3)

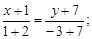
4)

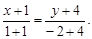
На рисунке 4 изображена прямая в отрезках по осям координат.

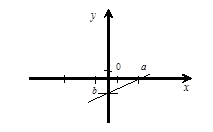
Рисунок 4

Данное уравнение имеет вид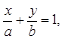

где a, b − отрезки, отсекаемые прямой на осях ОX, ОY соответственно.

Тест 12. На рисунке 5 изображена прямая.

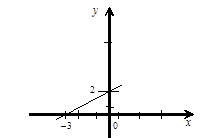
Рисунок 5

Данное уравнение имеет вид:

1)

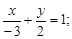
2)

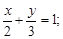
3)

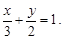
Общее уравнение прямой имеет вид ax + by + c = 0, где n = (a; b) − нормальный вектор прямой, т. е. вектор, перпендикулярный прямой.

Пример 8. Составить уравнение прямой, перпендикулярной вектору n = (2; –5) и проходящей через точку М(–4; 3).

Решение

Так как вектор n перпендикулярен прямой, то в общем уравнении прямой a = 2, b = –5, поэтому уравнение имеет вид 2x – 5y + c = 0. Точка М(–1; 3) принадлежит прямой, значит ее координаты обращают уравнение прямой в верное равенство, т. е. 2 × (–1) – 5 × 3 + с = 0. Откуда с = –17.

Ответ: 2x – 5y – 17 = 0.

Тест 13. Прямая –x + 4y + 9 = 0 перпендикулярна вектору:

1) (–1; 4);

2) (–1; 9);

3) (4; 9);

4) (4; –1).

Пусть даны две прямые 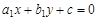и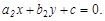

Тогда:

1) угол φ между ними вычисляется по формуле

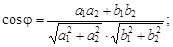
2) условие параллельности: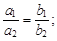

3) условие перпендикулярности: 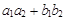= 0;

4) пересечение прямых: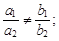

5) условие совпадения прямых: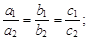

6) точкой пересечения прямых является решение системы их уравнений.

Тест 14. Прямая x – 2y + 5 = 0 параллельна прямой:

1) 2x + y + 5 = 0;

2) x + 2y + 4 = 0;

3) 3x – 6y + 1 = 0;

4) 5x – 10y + 5 = 0.

Тест 15. Прямая x – 2y + 5 = 0 перпендикулярна прямой:

1) x – 2y + 1 = 0;

2) 2x + y + 7 = 0;

3) x + 2y + 3 = 0;

4) x – 2y + 6 = 0.

Тест 16. Прямая x – 2y + 5 = 0 совпадает с прямой:

1) 3x + 6y + 15 = 0;

2) 5x – 10y + 25 = 0;

3) x + 2y + 5 = 0;

4) x – 2y + 6 = 0.

Тест 17. Угол между прямыми 3x – y + 1 = 0, –2x + 5y – 4 = 0 опре-
деляется по формуле:

1)

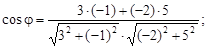
2)

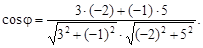
Каноническое уравнение прямой, проходящей через точку M₀(x₀; y₀) и параллельной направляющему вектору a = (m; n), имеет следующий вид:

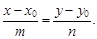
Очевидно, a × n = 0.

Пример 9.Найти уравнение прямой, перпендикулярной прямой
3x – y + 2 = 0 и проходящей через точку В(–1; 0).

Решение

Так как прямые перпендикулярны, то нормальный вектор одной является направляющим вектором другой. Значит, n = (3; –1) = a. Поэтому искомое уравнение имеет вид

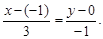
Преобразуем: –1(x + 1) = (y – 0) × 3, y =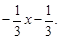

Ответ: y = .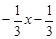

Тест 18. Уравнение прямой, параллельной вектору a = (–2; 4) и проходящей через точку М(3; –5), имеет вид:

1) ;

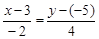2) x – 3 = y + 5;

3) .

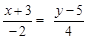Параметрические уравнения прямой, проходящей через точку M₀(x₀; y₀) и параллельной вектору a = (m; n), имеют вид

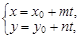, t Î R.

Тест 19. Направляющим вектором прямой 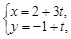, t Î R является:

1) a = (2; –1);

2) a = (3; 1);

3) a = (–3; –1).

Тест 20.Направляющим вектором прямой 3x – y + 5 = 0 является:

1)

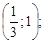
2) (3; –1);

3) ;

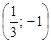4) (1; 3).

Расстояние от точки M₀(x₀; y₀) до прямой ax + by + c =0 определяется по формуле

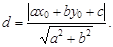
Пример 10. Найти длину высоты CD треугольника ABC с вершинами A(3; 0), B(–1; 2), C(4; –6).

Решение

Длина высоты треугольника ABC равна расстоянию от точки C до прямой AB.

Найдем уравнение стороны AB треугольника, используя уравнение прямой по двум точкам:

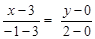, или 2(x – 3) = –4y, или 2x + 4y – 6 = 0.

Тогда длина высоты равна

= = = =

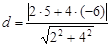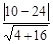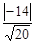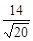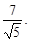
Тест 21. Расстояние от точки (4; –3) до прямой –x + 5y + 2 = 0 находится по формуле:

1)

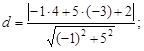
2)

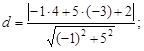
3)

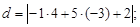
4)

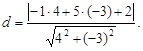
Ответы на тестовые задания

Номер теста
Правильный ответ

Номер теста
Правильный ответ