Методические указания к решению задачи. Брус, нагруженный парами сил, плоскости действия которых перпендикулярны его оси
Брус, нагруженный парами сил, плоскости действия которых перпендикулярны его оси, испытывает деформацию кручения и называется валом. Внутренним силовым фактором в поперечном сечении бруса в этом случае является крутящий момент MK , величину которого определяют методом сечений.
По этому методу крутящий момент в любом сечении вала численно равен алгебраической сумме крутящих моментов, расположенных по одну сторону от этого сечения. Крутящий момент, считается условно положительным, если при взгляде вдоль оси бруса с левого конца мы видим его направленным по ходу часовой стрелки.
Размеры и форма поперечного сечения вала в расчетах на кручение учитываются двумя геометрическими характеристиками: полярным моментом инерции 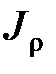 и полярным моментом сопротивления
и полярным моментом сопротивления 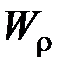 . Для круглого сечения они вычисляются по следующим формулам:
. Для круглого сечения они вычисляются по следующим формулам:
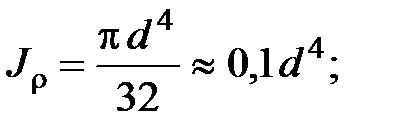
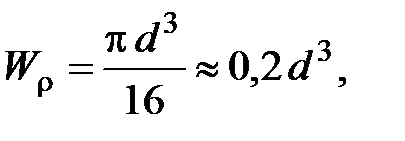
где d - диаметр сечения.
Крутящий момент MK вызывает в сечениях касательные напряжения τ , вычисляемых по формуле
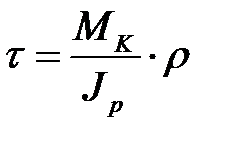 ,
,
где MK - крутящий момент в сечении бруса;
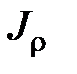 - полярный момент инерции сечения;
- полярный момент инерции сечения;
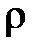 - расстояние от центра тяжести сечения до точки, в которой определяются напряжения.
- расстояние от центра тяжести сечения до точки, в которой определяются напряжения.
Условие прочности записывается в виде
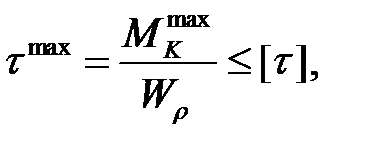
где 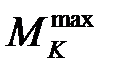 - максимальная по модулю величина крутящего момента, определяемого по эпюре
- максимальная по модулю величина крутящего момента, определяемого по эпюре 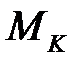 ;
;
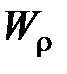 - полярный момент сопротивления;
- полярный момент сопротивления;
[t] - допускаемое касательное напряжение.
Деформация при кручении характеризуется углом закручивания j(рад):
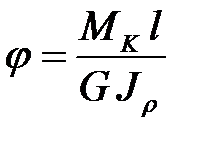 ,
,
где l - длина бруса;
G - модуль сдвига (модуль упругости второго рода).
Угол закручивания на единице длины бруса называется относительным углом закручивания и вычисляется по формуле
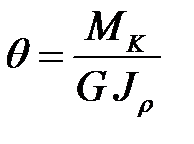 , (рад/м).
, (рад/м).
Условие жесткости накладывает ограничение на величину относительного угла закручивания:
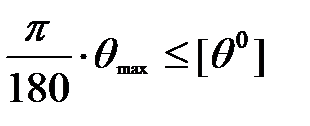 ,
,
где [q] - допускаемый угол закручивания в град/м.
Условие жесткости имеет вид
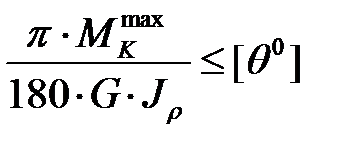 .
.
Пример решения задачи
Дано:К стальному валу кольцевого поперечного сечения с жесткой заделкой на одном конце приложены три внешних момента относительно продольной оси OX (рисунок 4.7).
Значения двух моментов заданы: M1=0,4кН·м, M2=2,0кН·м. Линейные размеры вала равны: а=b=c=1м. Отношение внутреннего и наружного диаметров сечения K=d/D=0,8; допускаемое касательное напряжение [τ]=40МПа; допускаемый относительный угол закручивания [θ]=0,5град/м, модуль сдвига стали G=0,8·105 МПа.
Требуется:
1) установить, при каком значении момента M3 исключается поворот свободного торцевого сечения.
2) определить величины крутящих моментов по участкам с учетом найденного значения M3 и построить их эпюры.
3) подобрать размеры кольцевого сечения по условиям прочности и жесткости вала.
Решение:
1. По исходным данным составляется расчетная схема вала с соблюдением масштаба (рисунок 4.2а).
2. Определяется неизвестный момент пары сил в концевом сечении.
Полагаем момент М3 положительным и известным М3=МХ.
Выделяем три расчетных участка, границами которых являются сечения, где появляется нагрузка (на рисунке участки KC, СВ и ВА. В пределах каждого проводится произвольное сечение.
| Рисунок 4.1 |
Определение неизвестного момента М3
Рассматривая от каждого сечения правую отсеченную часть (так как там нет опоры), вычисляем величины крутящих моментов, используя следующее рабочее правило, вытекающее из метода сечений:
Крутящий момент в любом сечении бруса численно равен алгебраической сумме моментов всех внешних сил, действующих по одну сторону от сечения относительно продольной оси бруса в месте сечения.
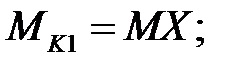
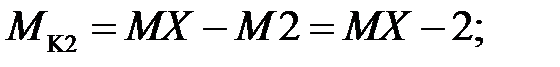
(пример определения MK2 представлен на рисунке 4.2, г)
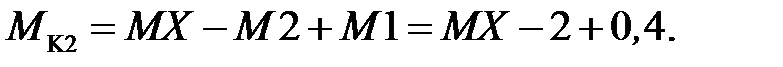
Эти значения моментов по расчетным участкам представлены на рисунке 4.2, б.
Угол закручивания i-го расчетного участка при постоянных характеристиках материала, сечения и нагрузки определяется по формуле:
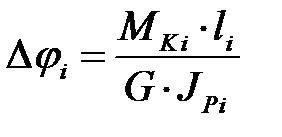 .
.
Сечение А в зоне заделки не закручивается. Перемещаясь по сечениям от зоны заделки вправо к свободному концу, имеем: 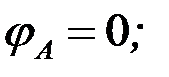
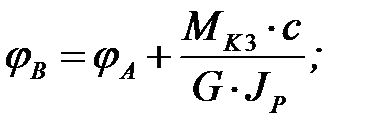
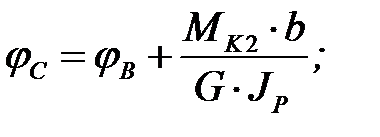
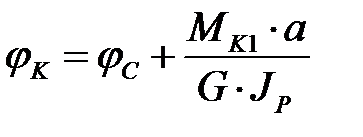 .
.
После подстановки известных значений и при условии, что поворот в торцевом сечении исключен (угол поворота равен нулю) получаем:
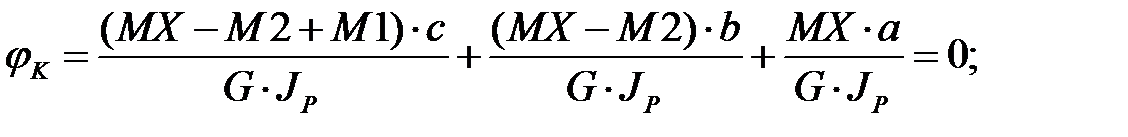
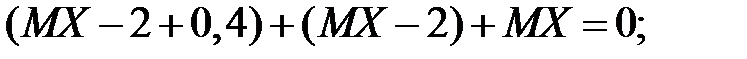
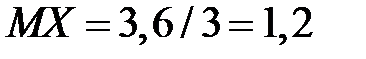 кН· м.
кН· м.
Определение величины крутящих моментов по участкам
Величины крутящих моментов по участкам вычисляем, используя рабочее правило метода сечений:
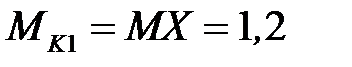 кН· м,
кН· м,
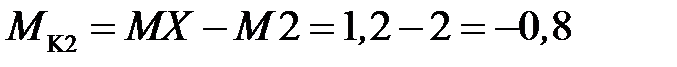 кН· м,
кН· м,
(пример определения MK2 представлен на рисунке 4.2, г)
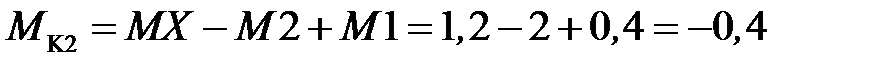 кН· м.
кН· м.
По этим значениям строим эпюры МК (см. рисунок 4.2, д).
Откуда получаем: 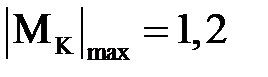 кН· м.
кН· м.
Подбор сечения по условию прочности
Определяется требуемый полярный момент сопротивления по условию прочности:
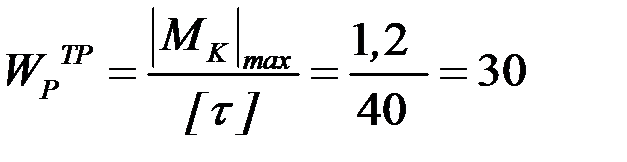 см3.
см3.
Полярный момент сопротивления для бруса кольцевого сечения равен: 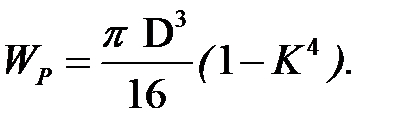
Приравниваем 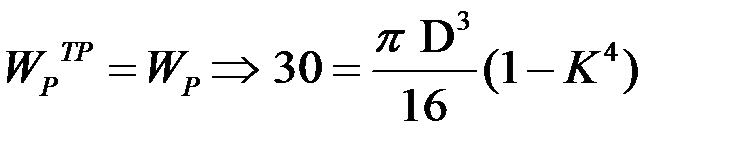 см3 .
см3 .
Отсюда при заданном К = 0,8 находим D = 6,37 см.
Подбор сечения по условию жесткости
Из условия жесткости 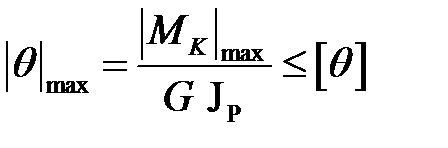 определяется требуемое значение полярного момента инерции по следующей формуле:
определяется требуемое значение полярного момента инерции по следующей формуле:
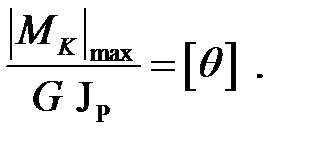
Откуда, 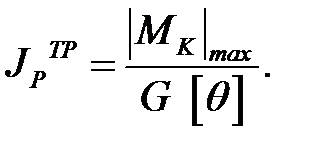
В это соотношение 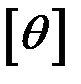 подставляется в радианах, поэтому заданный угол выразим в радианах:
подставляется в радианах, поэтому заданный угол выразим в радианах:
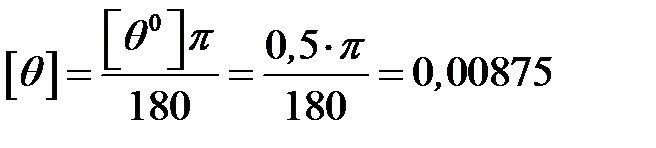 рад/м,
рад/м,
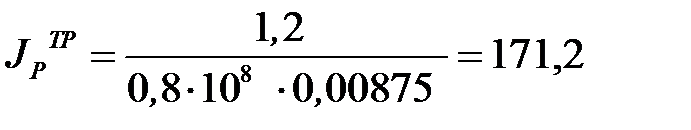 см4.
см4.
Из условия 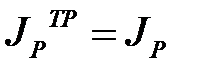 получим:
получим: 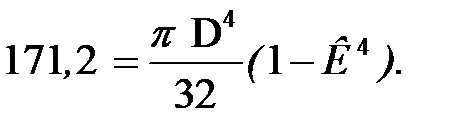
Отсюда, определяем D (по условию задачи К = 0,8):
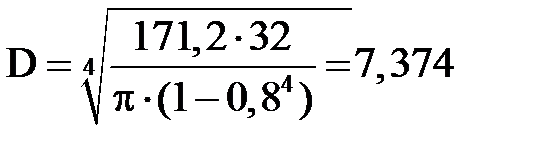 см.
см.
После округления примем D = 7,4 см, тогда,
d = 0,8 ×D = 0,8 × 7,4 = 5,92 см.
По результатам расчетов на прочность и жесткость видно, что по условию жесткости диаметр бруса требуется больше, чем по условию прочности (7,4 см > 6,37 см).
Окончательно принимаем больший диаметр:
D = 7,4 см, d = 5,92 см.
Рисунок 4.2
Проверка прочности и жесткости подобранного сечения
Предварительно определим полярный момент сопротивления и полярный момент инерции подобранного сечения:
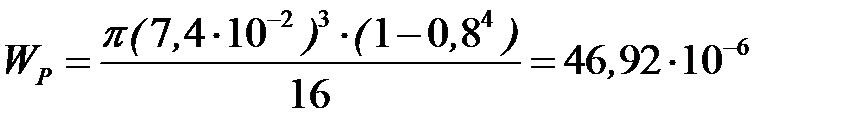 м3,
м3,
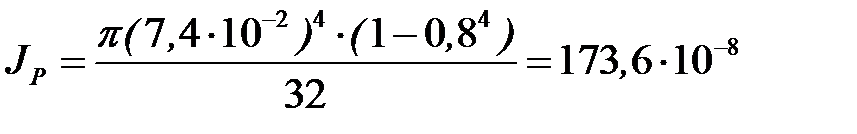 м4 ,
м4 ,
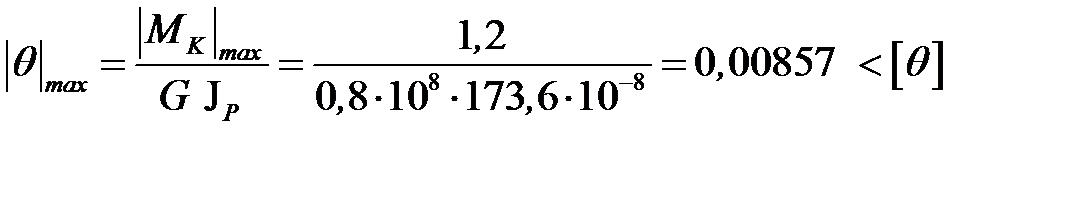 ,
,
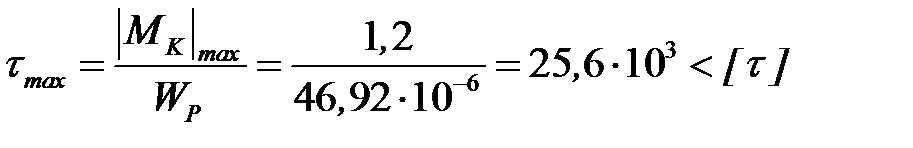 МПа.
МПа.
Условия прочности и жесткости выполняются.
Расчет вала круглого поперечного сечения производится аналогично, начиная с п.4.
Эпюра углов закручивания строится аналогично эпюре перемещений в задаче 1.1.
Вопросы и задания для самоконтроля
1. Как определяется внутренний крутящий момент в поперечном сечении вала? Какое принято правило знаков для крутящего момента?
2. Как распределяются касательные напряжения в круглом сечении вала? В чем преимущества использования полых валов?
3. Как записывается условие прочности вала при кручении? Какие основные задачи решаются при расчёте вала на прочность?
4. Что такое относительный угол закручивания? Как он вычисляется и какова его размерность?
5. Как определить угол закручивания участка вала постоянного сечения?
6. Как формулируется условие жёсткости для вала?
7. Как определяется диаметр вала из условия жесткости?
8. Как записывается закон Гука при чистом сдвиге?
Варианты тестовых заданий
| 4.1 | Чему равен наибольший по модулю крутящий момент? | |
| 4.2 | Чему равен крутящий момент на участке 3? | |
| 4.3 | Чему равен неизвестный крутящий момент? | |
| 4.4 | На каком участке вала деформация наибольшая, если размеры их считать одинаковыми? | |
| 4.5 | На каком участке вала деформация наименьшая, если размеры их считать одинаковыми? | |
| 4.6 | Укажите правильное распределение напряжений при кручении круглого вала. | |
| 4.7 | Укажите вариант рационального распределения моментов на валу. | |
| 4.8 | Укажите номер точки, где касательное напряжение при кручении наибольшее. | |
| 4.9 | Расположите номера точек в порядке убывания касательных напряжений при кручении. |
