Его свойства и применение
 Скалярным произведением двух ненулевых векторов
Скалярным произведением двух ненулевых векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла
называется число, равное произведению длин этих векторов на косинус угла  между ними (рис. 7):
между ними (рис. 7):
 .
.
Из рис. 7 видно, что 
 .Поэтому
.Поэтому  или
или  .
.
Скалярное произведение векторов обладает следующими свойствами:
1.  – переместительный закон;
– переместительный закон;
2.  – распределительный закон;
– распределительный закон;
3. Есливекторы 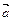 и
и 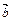 коллинеарны (
коллинеарны ( 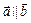 ), то
), то  ;
;
4. Есливекторы 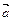 и
и 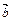 ортогональны (
ортогональны (  ), то
), то  (или
(или  или
или  );
);
 5. Скалярный квадрат вектора
5. Скалярный квадрат вектора  равен квадрату длины этого вектора
равен квадрату длины этого вектора  .
.
В частности, скалярное произведение единичных векторов (ортов) удовлетворяет равенствам (рис. 8):



В координатной форме скалярное произведение векторов 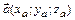 и
и  равно
равно  .
.
Пример 1.Найтидлину вектора  , если
, если  ,
,  ,
,  .
.
Решение. Воспользуемся пятым свойством скалярного произведения векторов:


 .
.
Применение скалярного произведения векторов.
1. Нахождение угла между векторами 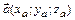 и
и  :
:
 .
.
Пример 2. Даны вершины треугольника  ,
,  и
и  . Найти внутренний угол при вершине С.
. Найти внутренний угол при вершине С.
Решение.Для нахождения угла  найдем координаты векторов
найдем координаты векторов  и
и  .
.

 ;
; 
 .
.
Тогда 
 . Таким образом,
. Таким образом,  .
.
Пример3.Найти проекцию вектора  на ось
на ось  , составляющую с координатными осями равные острые углы.
, составляющую с координатными осями равные острые углы.
Решение.Определим на оси  орт
орт  и найдем его координаты. Для этого воспользуемся тождеством
и найдем его координаты. Для этого воспользуемся тождеством  . Так как
. Так как  лежит на оси
лежит на оси  , то он образует с осями координат равные острые углы. Таким образом,Ða=Ðb=Ðg. Тогда тождество примет вид:
, то он образует с осями координат равные острые углы. Таким образом,Ða=Ðb=Ðg. Тогда тождество примет вид:
 , или
, или  . Это означает, что орт оси
. Это означает, что орт оси  имеет координаты
имеет координаты  .
.
Найдем косинус угла между ортом и вектором  :
:
 .
.
Тогда проекция вектора  на ось
на ось  будет равна
будет равна
 .
.
2. Нахождение проекции вектора на вектор. Пусть векторы заданы в координатной форме:  и
и  . Тогда проекции определяются формулами:
. Тогда проекции определяются формулами:
 ;
;
 .
.
Пример 4.Найти проекцию вектора  на вектор
на вектор  .
.
Решение.
 .
.
3. Проверка векторов на ортогональность. Два ненулевых вектора 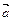 и
и 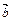 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда
 .
.
Пример 5.Даны вершины четырехугольника  ,
,  ,
,  ,
,  . Доказать, что его диагонали взаимно перпендикулярны.
. Доказать, что его диагонали взаимно перпендикулярны.
Решение. Найдем координаты векторов, определяющих диагонали четырехугольника  , или
, или  ;
;
 ,или
,или  . Проверим ортогональность этих векторов:
. Проверим ортогональность этих векторов:
 .
.
Это означает, что диагонали данного четырехугольникавзаимно перпендикулярны.
 4. Нахождение работы постоянной силы.* Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием силы
4. Нахождение работы постоянной силы.* Пусть материальная точка перемещается прямолинейно из положения А в положение В под действием силы  , образующей угол jс перемещением
, образующей угол jс перемещением  (рис. 9). Из курса физики известно, что работа силы
(рис. 9). Из курса физики известно, что работа силы  при перемещении
при перемещении  равна
равна  .
.
Таким образом, работа постоянной силы при прямолинейном перемещении ее точки приложения равна скалярному произведению вектора перемещения на вектор силы.
Пример 6.Вычислить работу, произведенную силой  ,если она имеет координаты
,если она имеет координаты  аточка ее приложения перемещается прямолинейно из положения А(2; 4; 6) в положение В(4; 2;7). Под каким углом к
аточка ее приложения перемещается прямолинейно из положения А(2; 4; 6) в положение В(4; 2;7). Под каким углом к  направлена сила
направлена сила  ?
?
Решение.Найдем перемещение материальной точки  .
.  , или
, или  .Тогда
.Тогда
 (ед. работы).
(ед. работы).
Угол jмежду  и
и  найдем поформуле
найдем поформуле

Литература: [ 1, гл. 5, § 5.7]; [2, гл. 18, § 12];[3, гл.2, п. 12.11];[4, гл. 2, §6].
