Построение матрицы с исходными данными

Лабораторная работа № 11

Тема: Экстремальные задачи на графах

Рассматриваемые вопросы:

- Основные понятия и определения теории графов

- Задача коммивояжера

Основные понятия и определения теории графов

Пусть А – множество состояний экономической системы. Отдельные состояния a_i называют элементами множества А, a_i Î A, A = {a_i}.

Рассмотрим два множества: A = {a_i}и B = {b_j}. Множество пар {(a_i, b_j)} называют декартовым произведением A ´ B.

Положим, B = A. Тогда A ´ B = A ´ A = {(a_i, b_j)} = A² – декартов квадрат. Подмножество R множества A², R Ì A², называют бинарным отношением на множестве А.

Пара множеств А и R называется графом состояний [A, R]. Элементы a_i называются вершинами графа, а пары вершин (a_i, a_j) – ребрами графа. Если ребра ориентированы, <a_i, a_j>, то их называют дугами. Граф с дугами называют ориентированным графом или орграфом, иначе граф называют обыкновенным.

Любой граф может быть представлен графически (для наглядности) или алгебраически (матрицей).

Пример. Пусть орграф из 7 вершин имеет 12 дуг: (1, 2), (1, 3), (1, 4), (1, 6), (2, 6), (2, 7), (3, 5), (3, 7), (4, 3), (4, 5), (5, 7), (6, 7).

Графическое представление (рис. 1).

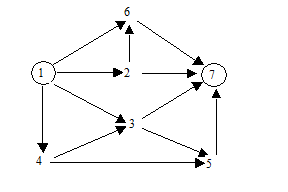
Рис.1

Матричное представление:

	×
		×
			×
				×
					×
						×
							×

Строки матрицы содержат исходящие дуги, а столбцы – входящие. Поэтому пустой столбец соответствует начальной вершине, а пустая строка – конечной. (Определение см. ниже.)

Последовательность вершин или дуг (ребер) графа, переводящая вершину a_i в вершину a_j, есть путь из a_i в a_j, S(a_i, a_j) = S_ij. Замкнутый путь S(a_i, a_i) в обыкновенном графе называется циклом, а в орграфе – контуром. В дальнейшем будут рассматриваться орграфы без контуров.

Всякая вершина в орграфе без контуров называется начальной – a₀, если она не имеет входящих дуг, и конечной – a_n, если она не имеет исходящих дуг.

Лемма. Всякий орграф без контуров обладает начальной и конечной вершинами.

Тогда процедура прохождения от а₀ к а_n или обратно (прямой или обратный ход) есть n-шаговый процесс, в котором один шаг соответствует прохождению одной дуги.

Задача коммивояжера

Одна из самых известных и важных задач транспортной логистики (и класса задач оптимизации в целом) – задача коммивояжера (англ. «Travelling salesman problem», TSP). Также встречается название «задача о бродячем торговце».

Суть задачи сводится к поиску оптимального, то есть кратчайшего пути проходящего через некие пункты по одному разу. Например, задача коммивояжера может применяться для нахождения самого выгодного маршрута, позволяющего коммивояжеру объехать определенные города со своим товаром по одному разу и вернуться в исходную точку.

Мерой выгодности маршрута будет минимальное время, проведенное в пути, минимальные расходы на дорогу или, в простейшем случае, минимальная длина пути. Кто и когда впервые начал исследовать задачу коммивояжера неизвестно, но одним из первых предложил решение подобной проблемы выдающийся математик XIX в. – Уильям Гамильтон. Мы рассмотрим замкнутый вариант задачи (т.е. такой, когда в итоге мы возвращаемся в исходную точку) и ее решение методом ветвей и границ.

Общий план решения задачи коммивояжера

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующий алгоритм :

1. Построение матрицы с исходными данными.

2. Нахождение минимума по строкам.

3. Редукция строк.

4. Нахождение минимума по столбцам.

5. Редукция столбцов.

6. Вычисление оценок нулевых клеток.

7. Редукция матрицы.

8. Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9.

9. Вычисление итоговой длины пути и построение маршрута.

Подробная методика решения задачи коммивояжера

В целях лучшего понимания задачи будем оперировать не понятиями графа, его вершин и т.д., а понятиями простыми и максимально приближенными к реальности: вершины графа будут называться «города», ребра их соединяющие – «дороги». Итак, методика решения задачи коммивояжера:

Построение матрицы с исходными данными

Сначала необходимо длины дорог соединяющих города представить в виде следующей таблицы:

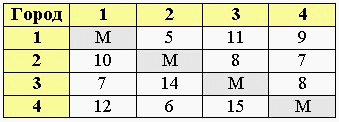
В нашем примере у нас 4 города и в таблице указано расстояние от каждого города к 3-м другим, в зависимости от направления движения (т.к. некоторые ж/д пути могут быть с односторонним движением и т.д.).

Расстояние от города к этому же городу обозначено буквой M. Также используется знак бесконечности. Это сделано для того, чтобы данный отрезок путь был условно принят за бесконечно длинный. Тогда не будет смысла выбрать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т.п. в качестве отрезка маршрута.