Как организовать эффект анимации отдельного объекта ?

IV. ЭТАП ПОДГОТОВКИ УЧАЩИХСЯ К АКТИВНОМУ И СОЗНАТЕЛЬНОМУ УСВОЕНИЮ НОВОГО МАТЕРИАЛА

Важно помнить, что широкое привлечение учащихся к самостоятельному приобретению знаний, овладению навыками и умениями, творческому применению их на практике невозможно без четкой целенаправленности этой работы, без постановки перед учащимися целей и задач каждого урока, показа практической значимости изучаемого материала.

Тематические и предметные интернет-ресурсы могут выступить как один из способов повышения интереса учеников. Наглядные пособия, телеконференции, видео и анимационные материалы – все это может показать новую тему учащимся с более понятной и интересной для каждого из них стороны. Такие ресурсы важно собирать и формировать «Библиотеку учителя на CD». В этом могут помочь дети. Как домашнее задание ребята получают следующую задачу: «В течение двух недель вы должны найти в Интернете 5 сайтов по теме «Производная в физике, технике, химии и экономике» и составить на каждый рецензию». Подготовить историческую справку по теме «Производная» с галереей портретов учёных-математиков.

V. ЭТАП УСВОЕНИЯ НОВЫХ ЗНАНИЙ

Условия достижения положительных результатов:

Применение различных способов активизации мыслительной деятельности учащихся, включение их в поисковую работу, в самоорганизацию обучения. Максимальное творческое участие детей.

Показатели выполнения учебно-воспитательной задачи этапа:

• качество ответов учащихся на следующих этапах урока;
• активное участие класса в проведении итогов беседы или самостоятельной работы.

Класс заранее разделён на 2 бригады, каждая из которых выполняет определённую подготовительную работу к уроку.

Первая бригада (из учащихся имеющих дома Интернет) выполняет поисковую работу в Интернете, о которой говорилось ранее.

Вторая бригада готовит дома формулы из физики и экономики, где используется производная.

υ(t) = х^/(t) – скорость

a (t)=υ^/ (t) - ускорение

J (t) = q^/(t) - сила тока

C(t) = Q^/(t) - теплоемкость

d(l)=m^/(l) - линейная плотность

K (t) = l^/(t) - коэффициент линейного расширения

ω (t)= φ^/(t) - угловая скорость

а (t)= ω^/(t) - угловое ускорение

N(t) = A^/(t) - мощность

П (t) = υ ^/ (t) - производительность труда,

где υ (t) - объем продукции

J(x) = y ^/ (x)- предельные издержки производства,

где y– издержки производства в зависимости от объема выпускаемой продукции x.

На данном этапе предлагается следующее:

Нам всем кажется, что в повседневной жизни мы великолепно обходимся без математики. Не правда, ли? Но это со всеми так. Сегодня на уроке мы убедимся в этом.

При решении и анализе задач используются готовые презентации, созданные учащимися, проводится аналитическое исследование процессов с помощью ОЭР «Интерактивная математика», «Математика 5-11 (Лаборатория)», «Школьный курс математики».

Покажем, что производная с нами присутствует целый день.

Исторические сведения

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

1) о разыскании касательной к произвольной линии

2) о разыскании скорости при произвольном законе движения

Еще раньше понятие производной встречалось в работах итальянского математика Тартальи (около 1500 - 1557 гг.) - здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л. Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Данные представлены на сайте, выполненном учащимися школы в программе

Физика

Решаем устно задачу № 1.

1. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 0⁰С до температуры t⁰ (по Цельсию), известно, что в диапазоне 0⁰ <= t <= 95⁰, формула Q (t) = 0,396t+2,081×10^-3t²-5,024×10^-7t³ дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.

Решение. C (t) = Q ^/ (t) = 0,396 + 4,162*10 ^-3 t – 15,072*10 ^-7 t²

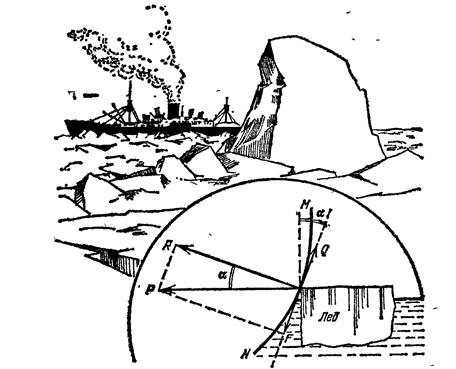
Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили.

Вот описание катастрофы: “Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу.

Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…”

Почему произошла катастрофа?

Сила Р давления льда (рис. на доске – плакат) разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – a – угол наклона борта к вертикали.

Q – сила трения льда о борт.

Q = 0,2 R (0,2 – коэффициент трения).

Если Q < F, то F увлекает напирающий лед под воду, лед не причиняет вреда, если Q > F, то трение мешает скольжению льдины, и лед может смять и продавить борт.

0,2R < R tg a , tg a > 0,2

Q < F, если a > 11⁰.

Наклон бортов корабля к вертикали под углом a > 11⁰ обеспечивает безопасное плавание во льдах.

(В это время на компьютере заставка – рисунок № 1).

Пришли в школу. Идут уроки. Кто на экономике, а кто – на технологии решает важные задачи. Задачу № 4 можно решить, рассмотрев по учебнику на стр. 136 (А.Н. Колмогоров “Алгебра и начала анализа 10–11”) вывод формулы в примере № 5.

Ответьте на вопрос: “О какой формуле идет речь?”

Задачу № 5 решаем самостоятельно.

5. Объем продукции V цеха в течение дня зависит от времени по закону V(t) = -5/3t³+15/2t²+50t+70, где 1 <= t <= 8. Вычислите производительность труда П при t =7 ч.

Решение:

П (t) = V ^/ (t)

П (t) = -5t² + 15t + 50

П (7) = -5*49 + 15*7 + 50 = - 90 (ед/ч)

Каков ответ в задаче?

Как можно объяснить, почему в ответе отрицательное число?

Закончились уроки.

Пришли домой, пообедали, отдохнули, выучили уроки и пошли играть на улицу. В снежки!

Задача № 7.

7. Высота снежка, брошенного вертикально вверх со скоростью U₀ с начальной высоты h_0, меняется по закону h =h₀+U₀*t-gt²/2, где g » 10м/c – ускорение силы тяжести. Покажите, что энергия камня Е=тv²/ 2 + mgh, где т – масса снежка, не зависит от времени.

(Учитель сам показывает решение).

Решение:

V (t) = h ^/ (t) = V₀ – gt

E = m/2 (V₀ - gt)² + mg(h₀ + V₀t – gt²/2) = mV₀²/2 + mgh₀

Наступил вечер. Вдруг отключился свет. Это значит, что сила тока равна нулю.

Задача № 6 (а и б)одновременно у доски два ученика.

6. Количество электричества, протекающее через проводник, задаётся формулой а) q(t) = t- O t+1: б) q(t) = t+4/t. В какой момент времени ток в цепи равен нулю?

а) Решение:

I(t) = q ^/ (t),

I(t) = 1 - 1/2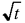

1 - 1/2 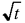=0

Отсюда, t = ? .

б) Решение:

I(t) = q ^/ (t),

I(t) = 1 - 4/t²

1 - 4/t² =0

Отсюда, t = 2 или t = -2; t = -2 не подходит по условию задачи