Операции над бинарными отношениями
Пусть f=(F,M) и r=(R,M) - два произвольных бинарных отношения.
Объединением бинарных отношений f иr называется бинарное отношение:
f  r=(F
r=(F  R, M), т.е. x(f
R, M), т.е. x(f  r)y тогда и только тогда, если имеет место либо xfy или xry.
r)y тогда и только тогда, если имеет место либо xfy или xry.
Пересечением бинарных отношений fи rназывается бинарное отношение :
fr=(F 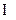 R, M), т.е. x(fr)y тогда и только тогда, если имеет место одновременно и xfy и xry.
R, M), т.е. x(fr)y тогда и только тогда, если имеет место одновременно и xfy и xry.
Разностью бинарных отношений fи rназывается бинарное отношение:
f\r=(F\R, M), т.е. x(f\r)y тогда и только тогда, если имеет место xfy и xr’y, где запись xr’y означает, что (x,y) 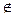 R.
R.
Дополнением к бинарному отношению fназывается бинарное отношение:
f’=( 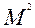 \F, M), т.е. xf’y тогда и только тогда, если (x,y)
\F, M), т.е. xf’y тогда и только тогда, если (x,y) 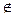 F.
F.
введенные операции над бинарными отношениями определяются через алгебраические операции над множествами. Так как бинарные отношения определяются как множества упорядоченных пар, то на них можно задавать и другие операции.
Произведением (композицией) бинарных отношений fи rназывается бинарное отношение f 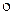 r =(F
r =(F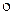 R, M), которое определяется следующим образом:
R, M), которое определяется следующим образом:
x(f 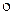 r)y тогда и только тогда, если множество M содержит хотя бы один элемент z
r)y тогда и только тогда, если множество M содержит хотя бы один элемент z
такой, что имеет место xfz и zry.
Симметрической частью бинарного отношения fназывается бинарное отношение 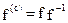 .
.
Асимметрической частью бинарного отношения fназывается бинарное отношение
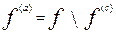 .
.
Выражение свойств бинарных отношений через задающие их множества.
Назовем бинарное отношение e =(E,M) единичным,если E={(x,y)| x=y, x  M}.
M}.
Необходимыми и достаточными условиями:
рефлексивностиявляется E  F;
F;
антирефлексивностиявляются EF=  ;
;
симметричностиявляется F= 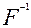 ;
;
антисимметричности является F 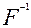
 E;
E;
асимметричностиявляется F 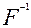 =
=  ;
;
транзитивностиявляется F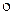 F
F  F;
F;
связностиявляется 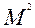 \E
\E  F
F
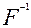 .
.
Отношения порядка. Упорядоченные множества.
Бинарное отношение f=(F,M) называется отношением строгого порядка,если оно антирефлексивно и транзитивно.
Бинарное отношение f=(F,M) называется отношением нестрогого порядка,если оно рефлексивно, транзитивно и антисимметрично.
Отношение строгого и нестрогого порядка называется отношением порядка.
Бинарное отношение порядка называется совершенным,если оно является связным.
Множество, для которого определено отношение порядка, называется множеством, упорядоченным этим отношением.
Если порядок, определенный на множестве, является совершенным, то множество называется линейно упорядоченнымили полностью упорядоченным множеством.
Если порядок не является совершенным, то множество называется частично упорядоченным.
