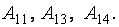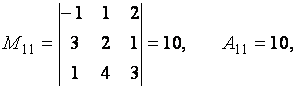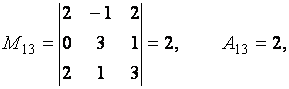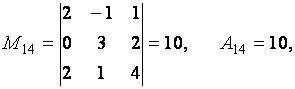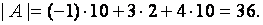Определитель квадратной матрицы
Определение 2.1. Подстановкой (перестановкой) множества 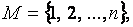 состоящего из
состоящего из 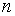 первых натуральных чисел, называется взаимно–однозначное отображение множества
первых натуральных чисел, называется взаимно–однозначное отображение множества 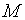 на себя. Число
на себя. Число 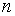 в этом случае называется порядком подстановки.
в этом случае называется порядком подстановки.
Подстановки будем записывать в виде таблицы, состоящей из двух строк и 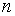 столбцов следующим образом:
столбцов следующим образом:
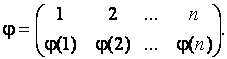
Пример. Примерами подстановок 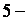 го порядка будут подстановки:
го порядка будут подстановки:
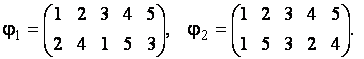
Теорема 2.1.Числоподстановок порядка 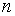 равно
равно 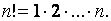
Пример. Подстановками третьего порядка будут следующие подстановки:
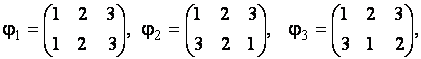
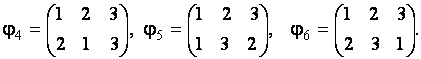
Определение 2.2. Подстановка множества 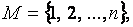 которая каждый элемент множества
которая каждый элемент множества 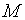 отображает сам в себя, называется тождественной подстановкой:
отображает сам в себя, называется тождественной подстановкой:
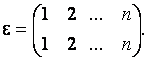
Определение 2.3. Произведением (композицией) подстановок
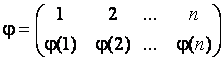 и
и 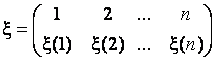
множества  называется подстановка этого множества, состоящая в последовательном выполнении указанных подстановок:
называется подстановка этого множества, состоящая в последовательном выполнении указанных подстановок:
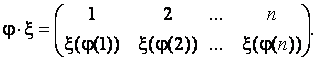
Пример. Найти произведения следующих подстановок третьего порядка:
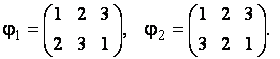
Воспользуемся определением 1.16 и запишем:
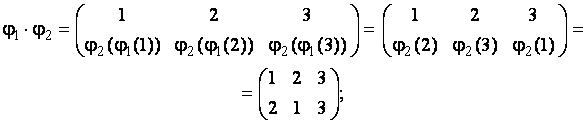
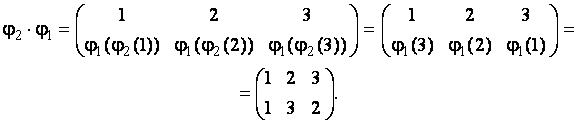
Замечание. Как следует из приведённого примера, произведение подстановок некоммутативно.
Определение 2.4. Пусть 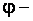 подстановка множества
подстановка множества 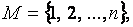 числа
числа 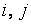 являются элементами множества
являются элементами множества 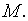 Пара чисел
Пара чисел 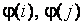 называется инверсией, если
называется инверсией, если 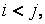 но при этом
но при этом 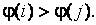
Пример. Вычислить количество инверсий подстановки седьмого порядка
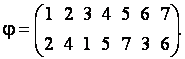
Для решения этой задачи воспользуемся определением 2.4 и подсчитаем количество пар 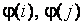 , для которых
, для которых 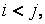 а
а 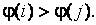
1) 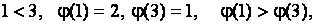
2) 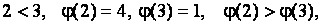
3) 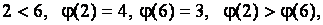
4) 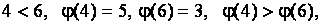
5) 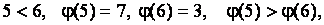
6) 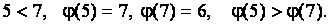
Таким образом, данная подстановка имеет 6 инверсий.
Определение 2.5. Определителемквадратной матрицы 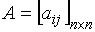 называется число, равное алгебраической сумме
называется число, равное алгебраической сумме 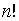 слагаемых, каждое из которых есть произведение
слагаемых, каждое из которых есть произведение 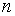 элементов матрицы, взятых по одному и только по одному из каждой строки и каждого столбца матрицы. Каждое произведение входит в сумму со знаком
элементов матрицы, взятых по одному и только по одному из каждой строки и каждого столбца матрицы. Каждое произведение входит в сумму со знаком 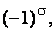 где
где 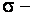 это число инверсий, образованных вторыми индексами элементов произведения при условии, что первые индексы расположены в порядке возрастания. Обозначается определитель матрицы
это число инверсий, образованных вторыми индексами элементов произведения при условии, что первые индексы расположены в порядке возрастания. Обозначается определитель матрицы 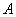 одним из следующих символов:
одним из следующих символов:
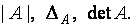
Для вычисления определителя квадратной матрицы, пользуясь определением 2.5, необходимо:
1) составить всевозможные произведения элементов матрицы, при этом взять только по одному элементу из каждой строки и каждого столбца;
2) определить знак каждого произведения, подсчитав число инверсий, образованных вторыми индексами элементов произведения при условии, что первые индексы расположены в порядке возрастания.
3) вычислить сумму всех найденных произведений.
Для квадратных матриц второго и третьего порядков существуют несложные правила вычисления их определителей.
Определитель квадратной матрицы 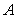 второго порядка вычисляется по формуле:
второго порядка вычисляется по формуле:

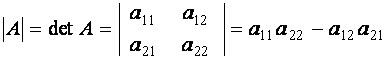 .
.
Определитель квадратной матрицы 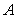 третьего порядка вычисляется по формуле:
третьего порядка вычисляется по формуле:

Формулу вычисления определителя матрицы третьего порядка удобно запоминать с помощью следующего мнемонического правила, которое схематично можно изобразить следующим образом (рис. 1) 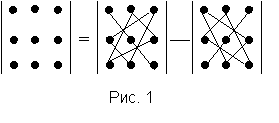 . SHAPE \* MERGEFORMAT
. SHAPE \* MERGEFORMAT
В соответствии с приведённой схемой, которая называется правилом треугольников, для вычисления определителя три произведения элементов матрицы следует взять со знаком «+» и три произведения – со заком «–».
Пример. Вычислить определитель матрицы 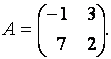
По формуле вычисления определителя квадратной матрицы второго порядка запишем:
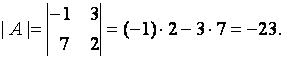
Пример. Вычислить определитель матрицы 
Воспользуемся указанной формулой:
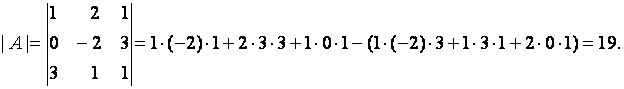
Теорема 2.2. Определитель квадратной матрицы обладает следующими основными свойствами:
1.При транспонировании матрицы её определитель не изменяется.
2.При сложении какой-либо строки (какого-либо столбца) матрицы, умноженной на любое действительное число, с другой строкой (с другим столбцом) матрицы определитель матрицы не изменяется.
3.Определитель матрицы, все элементы какой-либо строки (какого-либо столбца) которой равны нулю, равен нулю.
4.Определитель матрицы, имеющей две одинаковые строки (два одинаковых столбца), равен нулю.
5.Определитель матрицы, имеющей строки (столбцы), соответствующие элементы которых пропорциональны, равен нулю.
6.При замене местами двух строк (столбцов) матрицы определитель изменяет знак на противоположный.
7.При сложении одной строки (столбца) матрицы с другой строкой (столбцом), умноженной на действительное число k, отличное от нуля, величина её определителя изменится в k раз.
Замечание. Как следует из теоремы 2.2, некоторые элементарные преобразования матрицы изменяют величину её определителя.
Определение 2.6. Определитель матрицы, полученной из матрицы 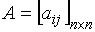 вычёркиванием
вычёркиванием 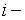 й строки и
й строки и 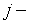 го столбца, называется минором элемента
го столбца, называется минором элемента 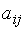 и обозначается символом
и обозначается символом 
Определение 2.7. Алгебраическим дополнением элемента 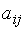 матрицы
матрицы 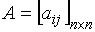 называется число, равное произведению минора этого элемента на
называется число, равное произведению минора этого элемента на 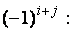
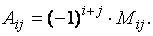
В частности, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, в которых находится элемент, есть число чётное, и с противоположным знаком, если это число нечётное.
Пример. Вычислить миноры и алгебраические дополнения элементов матрицы
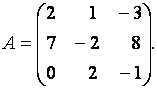
Для решения задачи воспользуемся определениями 2.6 и 2.7.
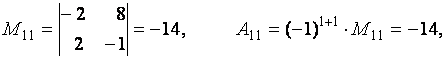
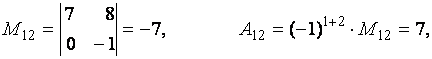
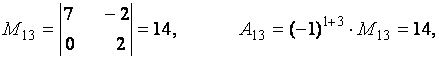
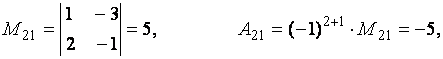
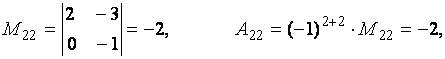
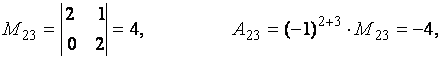
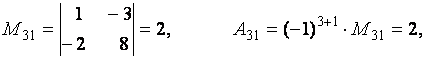
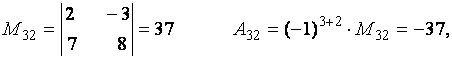
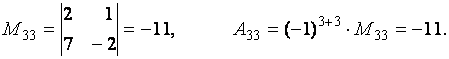
Теорема 2.3 (о разложении определителя по строке или столбцу). Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения:

Пример. Вычислить определитель матрицы 
Для вычисления определителя матрицы 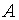 воспользуемся теоремой 2.3 и разложим определитель по элементам первой строки:
воспользуемся теоремой 2.3 и разложим определитель по элементам первой строки:
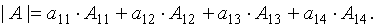
Поскольку 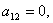 вычислим алгебраические дополнения
вычислим алгебраические дополнения