Сходящихся сил на плоскости
Распределенные силы.
В инженерных расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности тела по тому или иному закону.
Плоская система распределенных сил характеризуется ее интенсивностью q, т.е. значением силы, приходящимся на единицу длины нагруженного отрезка. Интенсивность измеряется в ньютонах, деленных на метр (Н/м).
Силы, равномерно распределенные вдоль отрезка прямой. Для такой системы сил интенсивностьq имеет постоянное значение. При статических расчетах эту систему сил можно заменить равнодействующей по модулю Q=q*l , приложенной в середине отрезка длинной l.
Силы, распределенные вдоль отрезка прямой по линейному закону. Примером такой нагрузки могут служить силы давления воды на плотину, имеющие наибольшее значение у дна и падающие до нуля у поверхности воды. Для этих сил интенсивность q является величиной переменной, растущей от нуля до максимального значения qmax.Равнодействующая по модулю Q=0,5 qmax*l , приложенной в точке пересечения медиан углов – на расстоянии 1/3l от точки с максимальным значением q.
Аналитический способ определения равнодействующей
сходящихся сил на плоскости.
Система сходящихся сил в общем случае приводится к одной - равнодействующей этой системе сил. Для аналитического определения равнодействующей силы следует выбрать систему прямоугольных осей координат и воспользоваться теоремой из геометрии о том, что проекция замыкающей любого многоугольника на какую-либо ось равна алгебраической сумме проекций составляющих его сторон на ту же ось. Равнодействующая сила при равновесии системы 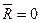 является замыкающей силового многоугольника, или векторной суммой сил, но, с другой стороны,
является замыкающей силового многоугольника, или векторной суммой сил, но, с другой стороны, 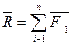 .
.
Проецируя векторы векторного равенства на прямоугольные оси координат, согласно теореме о проекции замыкающей получим 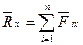 получаем условия равновесия системы сходящихся сил в аналитической форме
получаем условия равновесия системы сходящихся сил в аналитической форме 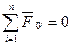 , т. е. для равновесия системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координат осей, лежащих в плоскости, были равны нулю. Уравнением равновесия сил является выражение
, т. е. для равновесия системы сходящихся сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных координат осей, лежащих в плоскости, были равны нулю. Уравнением равновесия сил является выражение 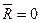 .
.
Примеры на применение условия равновесия пар на плоскости.
Задача. Двухконсольная горизонтальная балка шарнирно закреплена в точке А и опирается на катки в точке В (рис. 1.4а). На балку действует вертикальная сила Q = 20 Н, приложенная в точке D, равномерно распределенная вертикальная нагрузка на участке ВС интенсивностью р = 25 Н /м и пара сил ( N,N'), момент которой равен т = 40 Нм. Расстояния: АО = 3 м, АВ = 4 м, ВС= 3 м. Определить реакции в шарнирах А и В, пренебрегая весом балки.
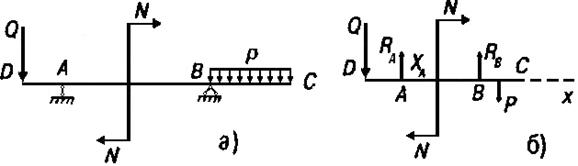
Рисунок 1.2.1
Решение. Отбросим связи, которыми в данной задаче являются опоры А и В, и заменим их реакциями (рис. 1.2.1.б). Реакция в точке В направлена по вертикали и обозначена RB. Она направлена по вертикали, так как опора В опирается на катки и не препятствует перемещению по горизонтали. Реакция шарнира А может иметь любое направление в плоскости. Поэтому заменяем ее двумя составляющими ХА и YA. Распределенную нагрузку р заменяем силой Р = р х ВС = = 25 х 3 = 75 Н. Сила приложена посредине отрезка BС Выбираем оси координат: ось х направляем из точки D вдоль балки, ось у – из точки D перпендикулярно балке вверх.
Так как проекция силы ХA является единственной силой, проектирующейся на ось Х , то при равновесии сил, приложенных к балке, она равна нулю: ХA = 0. Заметим, что сумма проекций сил (N, N'), образующих пару сил, на любую ось равна нулю, так как силы, образующие пару сил, равны по модулю, параллельны и направлены в противоположные стороны. Переходим к составлению уравнений равновесия для системы параллельных сил, приложенных к балке. Сумма проекций всех сил на ось у равна нулю: УA+ RB- Q- Р= 0. Сумма моментов всех сил относительно точки А (удобно выбирать точку, к которой приложена одна из неизвестных сил, тогда получим уравнение с одним неизвестным) также равна нулю: Q х AD – т + R х АВ – Р (АВ + ВС/ 2) = 0. Решая ее, получим RB= 98,1 Н. Находим Y =Q+р – RB= 20 + 75 – 98,1 = -3,1 H. Знак «-» показывает, что реакция направлена вниз.
Задача. Балка АВ весом Р и длиной / заделана правым концом в стену. В точке А на балку действует вертикальная сила F. Определить реакцию стены.
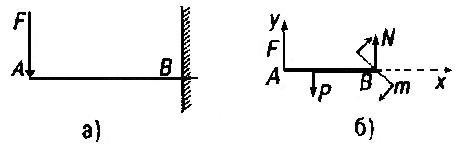
Рисунок 1.2.2.
Решение. Отбросим связь - стену и заменим ее действие реакцией (рис. 1.2.2.б). Горизонтальная составляющая реакции стены равна в данном случае нулю, так как все активные силы, действующие на балку, вертикальны. Реакция стены состоит из вертикальной составляющей N пары сил с моментом т. Эта пара сил препятствует повороту балки против хода часовой стрелки. Такой поворот балка стремится осуществить под действием сил F u P. Переходим к составлению уравнений равновесия. Выбираем оси координат; ось х направляем по балке АВ, ось у - по вертикали из точки А. Приравниваем нулю сумму проекций всех сил на ось y 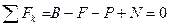 . Приравниваем к нулю сумму моментов всех сил относительно точки В:
. Приравниваем к нулю сумму моментов всех сил относительно точки В: 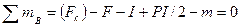 . Из первого уравнения находим N = F+ Р. Из второго уравнения определяем момент пары сил т = FI+ PI/2.
. Из первого уравнения находим N = F+ Р. Из второго уравнения определяем момент пары сил т = FI+ PI/2.
