Перестановки с повторениями

Рассматривая различные перестановки, мы предполагали, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам.

Если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., n_k элементов к-го вида, то имеем перестановки с повторениями, их число:

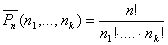, где n₁+…+n_k = n.

Задача: сколько различных «слов» можно составить из букв слова ДЕД, МАТЕМАТИКА.

Решение: имеем перестановки с повторениями.

А) ДЕД n=3, k=2, n₁=2, n₂=1

P₃(2, 1) = 3!/(2! • 1!) = 6 / 2 = 3;

Б) МАТЕМАТИКА n=10, k=6, n₁=2, n₂=3, n₃=2, n₄=n₅=n₆=1

P₁₀(2,3,2,1,1,1)=10!/(2! • 3! • 2!)=2•4•5•6•7•9•10 = 134 400.

Размещения

1) Размещения без повторений.

Размещениями называют комбинации, составленные из n данных элементов по k элементов (k<=n, k>0), которые отличаются либо составом элементов, либо порядком расположения элементов. Обозначаются размещения A_n^k . А - первая буква французского слова arrangement, что в переводе означает "размещение", "приведение в порядок". Число всех возможных размещений находится по формуле:

.

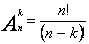Задача: расписание одного дня состоит из двух пар. Определить число вариантов расписания при выборе из пяти дисциплин, если не может быть одинаковых пар.

Решение: имеем размещения без повторений из пяти элементов по два, из число: .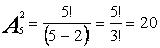

2) Размещения с повторениями.

Пусть существуют n различных элементов. Выберем из них m штук, действуя по следующему принципу: возьмем любой элемент, но не будем устанавливать его в какой-либо ряд, а просто запишем под номером 1 его название, сам же элемент вернем к остальным элементам. Затем опять из всех n элементов выберем один, запишем его название под номером 2 и снова вернем элемент обратно. Будем выполнять эти операции, пока не получим m названий. Размещения с повторениями вычисляются по формуле:

.

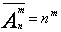Задача: сколько четырехзначных номеров можно составить из 10 цифр?

Решение: имеем размещения с повторениями из 10 элементов по 4, их число: .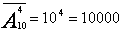

Сочетания

1) Сочетания без повторений.

Сочетаниями называют комбинации, составленные из n различных элементов по k (k =< n) элементов, которые отличаются хотя бы одним элементом. Сочетания обозначаются: C_n^k C - первая буква французского слова combinasion - сочетание.

Составим из n элементов всевозможные сочетания по k элементов в каждом. Их будет C_n^k . Внутри каждого сочетания, состоящего из k элементов, образуем всевозможные комбинации, учитывающие порядок следования в них элементов. Таких комбинаций будет P_k, т.к. мы в нашем сочетании образовываем перестановки. Всего различных комбинаций из n элементов по k в каждой, отличающихся друг от друга либо составом (элементами), либо порядком их следования, будет C_n^k • P_k . Но такие комбинации называются размещениями. Таким образом, A_n^k = C_n^k • P_k, тогда:

.

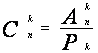Задача: в шахматном турнире участвует 7 человек; сколько партий будет сыграно, если между любыми двумя участниками должна быть сыграна партия?

Решение: имеем сочетания без повторений из 7 элементов по 2; их число: 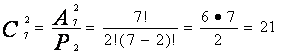.