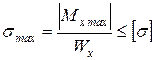Задача 3. Расчёт статически неопределимого

Ступенчатого бруса при растяжение (сжатие)

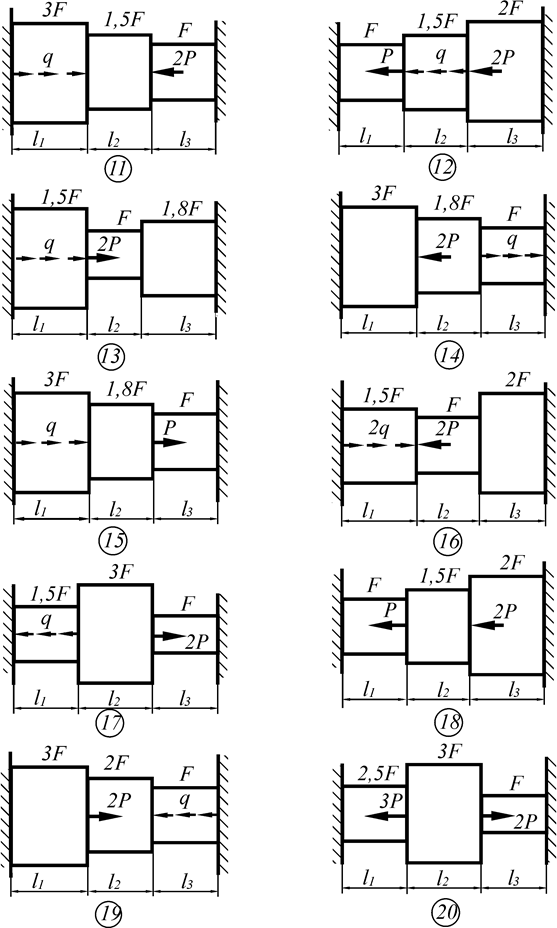
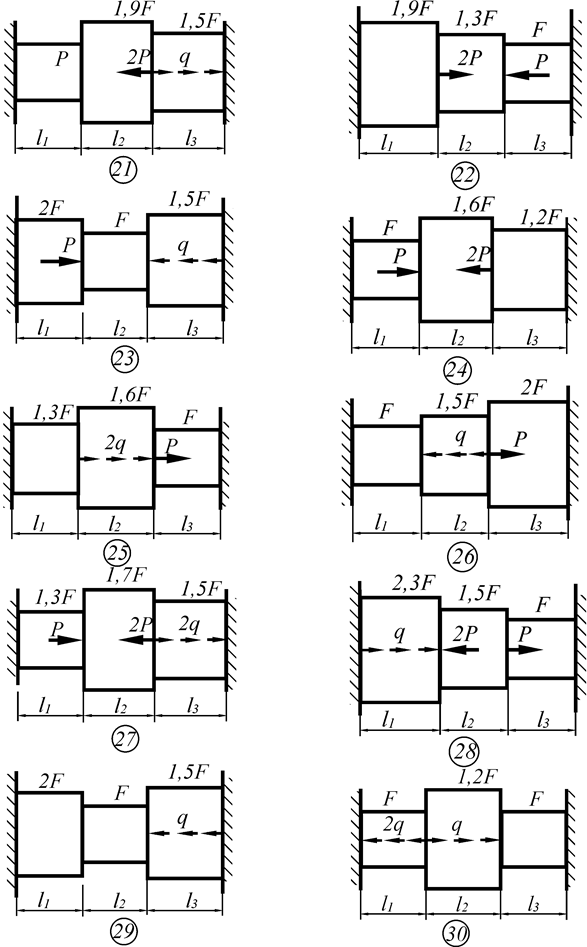
Для статически неопределимого бруса с жёстко защемлёнными концами, нагруженного продольной нагрузкой как показано на схеме к задаче 3 необходимо:

1. Построить эпюры продольных сил N, нормальных напряжений 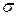и перемещений ;

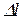2. Подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок,

Необходимые данные для решения задачи взять из таблицы1.3.

Таблица 1.3

Вариант	Усилия	Длины участков
Р, кН	q,кН/м	l1, м	l2, м	l3, м
	27	12		2	0,5
	35	24	1,2	1,9	0,8
	53	46	1,3	1,8	1
	29	10	1,4	1,7	1,1
	37	22	1,5	1,2	1,2
	45	32	1,6	1,4	2
	10	30	1,7	1	1,8
	15	18	1,8	1,1	1,5
	25	20	1,9	1,2	1,2
	50	44	2	0,8	1

Схемы к задаче 3

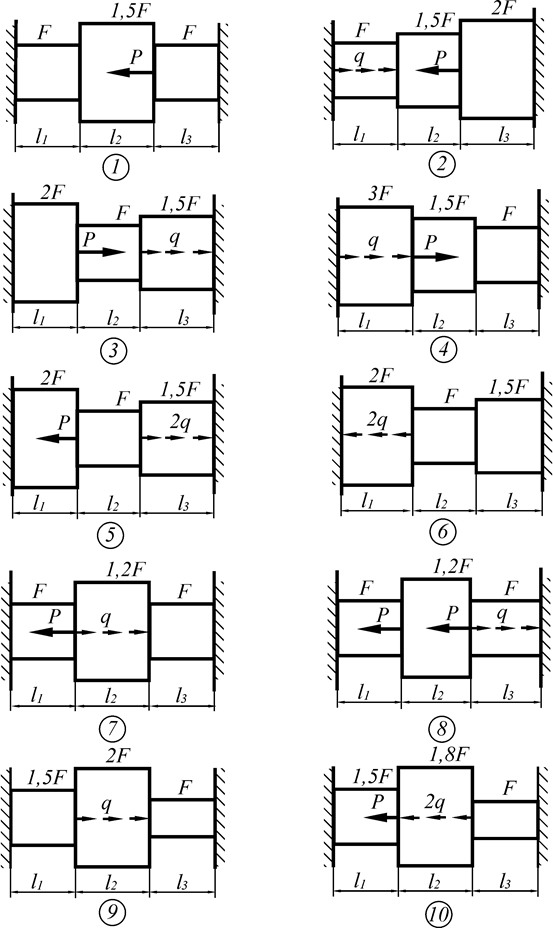
Схемы к задаче 3

Схемы к задаче 3

Пример решения задачи 3

Для ступенчатого бруса (см. рис. 1.5а) построить эпюры продольных сил N, нормальных напряжений 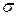и перемещений 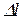; подобрать величину площади поперечных сечений всех участков бруса методом допускаемых нагрузок если Р₁=3Р; Р₂=2Р.

Р=10 кН, а=1м,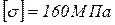

Решение

Задача один раз статически неопределима в силу плоской системы сил, действующих по одной прямой, для которой, как известно, можно составить только одно уравнение равновесия:

,

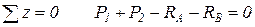в котором два неизвестных: 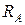и .

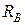Отбросим правую опору, заменив её действие на брус реакцией .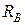

Перемещение сечения в точке В равно нулю, т.к. это сечение жёстко заделано. Используя принцип независимости действия сил, получим уравнение совместности деформаций:

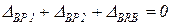
Распишем эти деформации по закону Гука:

,

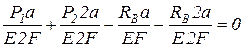отсюда, после сокращения на а и EF, 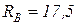кН.

В соответствии с расчётной схемой рис. 1.5б аналитические зависимости для N, 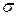и 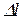будут следующими:

Участок 1

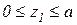
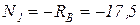кН ; ; .

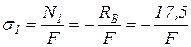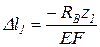Подставим в уравнение для перемещения два крайних значения 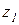, после подстановки будем иметь:

.

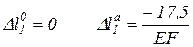Участок 2

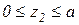
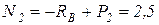кН;

;

.

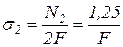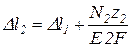Подставляя пределы получим:

.

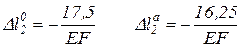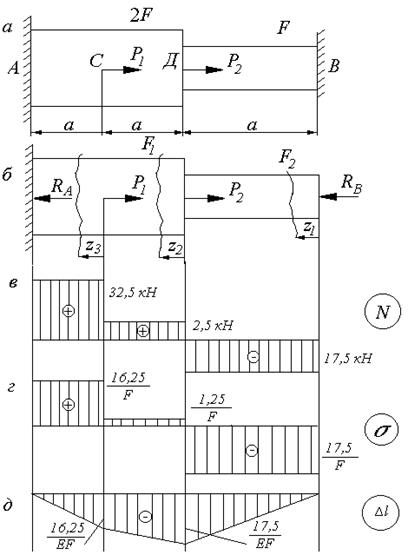
Рис. 1.5 Расчётная схема и эпюры для примера

решения задачи 3

Участок 3

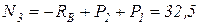кН;

;

.

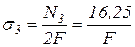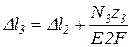Подставляя пределы получим:

.

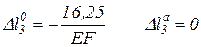На основании данных аналитических зависимостей строим эпюры N, 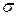и 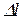(рис. 1.5 в, г,д).

Построение эпюры перемещений может служить проверкой правильности решения задачи. Перемещение на участке 1 при z₁=0 равно нулю, перемещение на участке 3 при z=a также должно равняться нулю, т.к. эти два сечения соответствуют жёсткому закреплению бруса, перемещения которых невозможны.

2. На эпюре нормальных напряжений найдём максимальное напряжение: .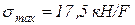

Для определения площади поперечного сечения воспользуемся условием прочности по нормальным напряжениям:

.

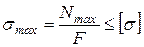Приравняв максимальное нормальное напряжение к допускаемому, определим площадь поперечного сечения F:

.

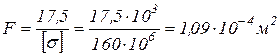Таким образом, на участке 1 площадь поперечного сечения должна быть 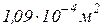, а на участке 2 в два раза больше, т.е. .

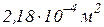Плоский изгиб

Изгиб называется плоским, если плоскость действия изгибающей нагрузки проходит через главную центральную ось инерции сечения.

Если изгибающий момент M_x является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы Q_y изгиб называется поперечным.

Брус, работающий при изгибе, называется балкой.

Построение эпюр поперечной силы Q_y и изгибающего момента M_x является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Q_y и M_x определяется опасное сечение, т.е. сечение в котором может произойти разрушение.

Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения .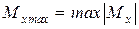

В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила .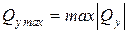

Между поперечной силой и изгибающим моментом существует следующая зависимость:

,

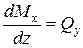то есть первая производная от изгибающего момента по длине участка равна поперечной силе.

Это соотношение в общем виде было получено Журавским и носит название теоремы Журавского.

На основании теоремы Журавского могу быть сформулированы правила проверки эпюр:

1. В точке приложения сосредоточенной силы на эпюре Q_y должен быть скачок, равный по величине и знаку приложенной силе.

2. В точке приложения сосредоточенного момента на эпюре M_x должен быть скачок, равный по величине и по знаку приложенному моменту.

3. На участке, где приложена распределенная нагрузка, эпюра Q_y является наклонной прямой (наклон по направлению действия нагрузки), а эпюра M_x - параболой, выпуклость которой направлена навстречу распределенной нагрузке.

4. На участках, где Q_y > 0, M_x возрастает, на участках, где Q_y< 0, M_x убывает, если Q_y = 0 (эпюра пересекает нулевую линию), то эпюра М_x имеет экстремум.

5. В тех точках, где на эпюре Q_y имеется скачок, на эпюре М_x будет излом.

6. Чем больше по модулю величина Q_{y ,} тем круче изменяется эпюра М_x.

7. На свободных концах балки изгибающий момент равен нулю.

Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении

.

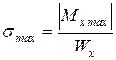Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений