Задача 2. Расчет вала на прочность при кручении
Сопротивление материалов
Задача 1. Расчет стержней при центральном растяжении ( сжатии).
Стальной стержень (модуль Юнга 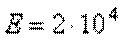 кН/см2) с размерами
кН/см2) с размерами 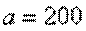 см;
см; 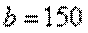 см,
см, 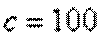 см и площадью поперечного сечения нижнего участка
см и площадью поперечного сечения нижнего участка 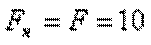 см2, а верхнего –
см2, а верхнего –  см2 нагружен внешними осевыми силами
см2 нагружен внешними осевыми силами 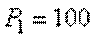 кН и
кН и  кН (см. рис.). Построить эпюры продольных сил
кН (см. рис.). Построить эпюры продольных сил 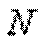 и нормальных напряжений
и нормальных напряжений  . Оценить прочность стержня, если предельное напряжение (предел текучести)
. Оценить прочность стержня, если предельное напряжение (предел текучести) 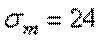 кН/см2, а допускаемый коэффициент запаса
кН/см2, а допускаемый коэффициент запаса 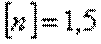 . Найти удлинение стержня
. Найти удлинение стержня 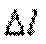 .
.
| № вар. | а | b | c | Fн | Fв | P1 | P2 |
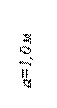
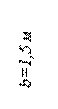
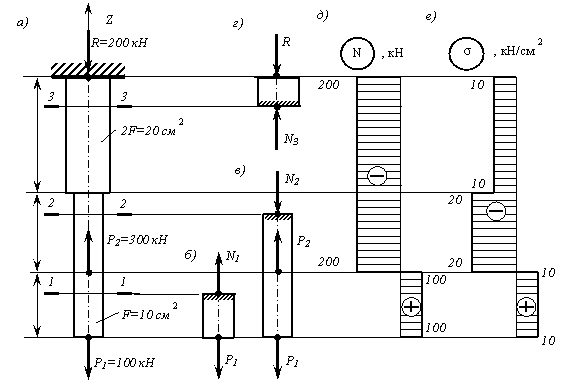
Решение.
1.Определяем значение опорной реакции 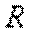 , возникающей в заделке.
, возникающей в заделке.
Учитывая, что 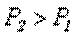 , направим опорную реакцию
, направим опорную реакцию 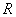 вниз. Тогда из уравнения равновесия
вниз. Тогда из уравнения равновесия 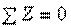 находим:
находим:
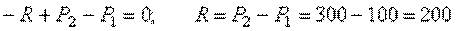 кН.
кН.
2.Строим эпюру продольных сил 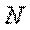 .
.
Разбиваем длину стержня на три участка (рис. а). Границами участков являются те сечения, в которых приложены внешние силы и (или) изменяется размер поперечного сечения стержня.
Воспользуемся методом сечений (РОЗУ). Делаем по одному сечению в произвольном месте каждого из трех участков стержня.
Начнем с сечения 1 – 1. Отбросим (или закроем листком бумаги) верхнюю часть стержня (рис. б). Само сечение 1 – 1 мысленно считаем неподвижным. Мы видим, что внешняя сила  растягиваетрассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой
растягиваетрассматриваемую нижнюю часть стержня. Отброшенная нами верхняя часть стержня противодействует этому растяжению. Это противодействие мы заменим внутренней продольной силой 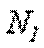 , направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила
, направленной от сечения и соответствующей растяжению. Разрушения стержня не произойдет только в том случае, если возникающая в сечении 1 – 1 внутренняя продольная сила 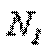 уравновесит внешнюю силу
уравновесит внешнюю силу 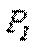 . Поэтому очевидно, что
. Поэтому очевидно, что
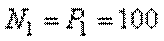 кН.
кН.
Переходим к сечению 2 – 2 (рис. в). Внешняя сила  растягивает рассматриваемую нами нижнюю часть стержня, а сила
растягивает рассматриваемую нами нижнюю часть стержня, а сила 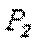 ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи,
ее сжимает (напомним, что 2 – 2 мы мысленно считаем неподвижным). Причем, согласно условию задачи, 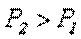 . Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила
. Чтобы уравновесить эти две силы, в сечении 2 – 2 должна возникнуть внутренняя сила 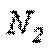 , противодействующая сжатию, то есть направленная к сечению. Она равна:
, противодействующая сжатию, то есть направленная к сечению. Она равна:
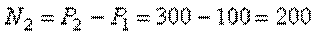 кН.
кН.
Делаем сечение 3 – 3 (рис. г). Отбросим теперь часть стержня, расположенную ниже этого сечения. Внутренняя продольная сила 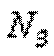 должна уравновесить внешнюю (реактивную) сжимающуюсилу R. Поэтому она направлена к сечению и равна:
должна уравновесить внешнюю (реактивную) сжимающуюсилу R. Поэтому она направлена к сечению и равна:
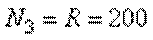 кН.
кН.
Легко убедиться в том, что полученный результат не изменится, если мы отбросим не нижнюю, а верхнюю часть стержня. В этом случае продольная сила 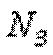 также противодействует сжатию. Она равна:
также противодействует сжатию. Она равна:
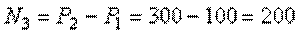 кН.
кН.
При построении эпюры продольных сил 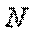 будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.
будем пользоваться следующим правилом знаков: внутренняя продольная сила, возникающая в поперечном сечении стержня, считается положительной, если она противодействует растяжению стержня, и отрицательной, если она противодействует его сжатию.
Это правило знаков вводится для того, чтобы можно было наглядно видеть, какая часть стержня испытывает деформацию растяжения, а какая часть – деформацию сжатия. Это обстоятельство может оказаться крайне важным, в частности для стержней из хрупкого материала, которые имеют разные допускаемые напряжения на растяжение и на сжатие.
Таким образом, мы установили, что в любом сечении нижнего участка стержня внутренняя продольная сила противодействует растяжению и равна  кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому
кН. В любом сечении среднего и верхнего участков стержня имеет место деформация сжатия, поэтому 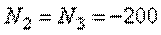 кН.
кН.
Для построения эпюры продольных сил 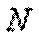 проводим тонкой линией ось, параллельную оси стержня z (рис. д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
проводим тонкой линией ось, параллельную оси стержня z (рис. д). Вычисленные значения продольных сил в выбранном масштабе и с учетом их знака откладываем от этой вертикальной оси. В пределах каждого из участков стержня продольная сила остается постоянной, поэтому мы как бы «заштриховываем» горизонтальными линиями соответствующий участок.
Отметим, что каждая линия «штриховки» (то есть ордината эпюры) в принятом масштабе дает значение продольной силы в соответствующем поперечном сечении стержня.
Полученную эпюру обводим жирной линией.
Анализируя полученную эпюру, мы видим, что в местах приложения внешних сил на эпюре 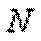 имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. д, никак не сказывается на характере эпюры
имеет место скачкообразное изменение продольной силы на величину, равную значению соответствующей внешней силы. Причем изменение поперечного размера стержня, как это видно из рис. д, никак не сказывается на характере эпюры 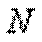 .
.
3. Строим эпюру нормальных напряжений  .
.
Нормальное напряжение, возникающее в k–м поперечном сечении стержня при растяжении (сжатии), вычисляется по следующей формуле
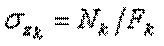 ,
,
где 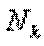 и
и 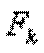 – продольная сила и площадь k–го поперечного сечения стержня соответственно.
– продольная сила и площадь k–го поперечного сечения стержня соответственно.
В первом поперечном сечении стержня нормальное напряжение равно
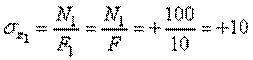 кН/см2,
кН/см2,
во втором –
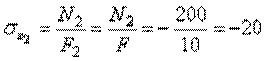 кН/см2,
кН/см2,
в третьем –
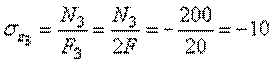 кН/см2.
кН/см2.
Строим по вычисленным значениям эпюру 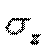 (рис. е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре
(рис. е). В пределах каждого из участков стержня напряжения постоянны, то есть эпюра напряжений параллельна оси. Заметим, что в отличие от эпюры N, на эпюре 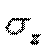 «скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
«скачок» имеет место не только в местах приложения внешних сил, но и там, где происходит изменение размеров поперечного сечения стержня.
4. Оцениваем прочность стержня.
Сопоставляем наибольшее (по модулю) нормальное напряжение 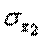 , которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением
, которое в нашем примере возникает во втором сечении стержня, с допускаемым напряжением 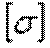 .Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения
.Напомним, что допускаемое напряжение представляет собой долю от предельного напряжения 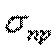 , то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести:
, то есть от напряжения, при котором начинается разрушение материала. Разрушение стали, как пластичного материала, начинается при появлении значительных остаточных деформаций. Поэтому для стали предельное напряжение равно пределу текучести: 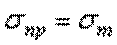 . Тогда
. Тогда
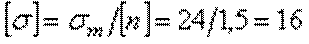 кН/см2.
кН/см2.
Условие прочности имеет вид 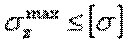 . В нашем случае
. В нашем случае
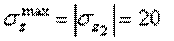 кН/см2 >
кН/см2 > 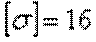 кН/см2,
кН/см2,
следовательно, прочность стержня на втором участке не обеспечена.
Таким образом, площадь поперечного сечения стержня на втором участке, равную 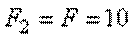 см2, нам необходимо увеличить.
см2, нам необходимо увеличить.
Несложный анализ показывает, что на других участках стержня условие прочности выполняется.
Из условия прочности определяем требуемую площадь поперечного сечения стержня на втором участке:
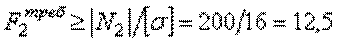 см2.
см2.
Принимаем на втором участке 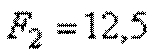 см2.
см2.
5. Вычисляем удлинение всего стержня 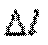 .
.
При переменных по длине стержня значениях продольной силы и площади поперечного сечения удлинение вычисляется по формуле
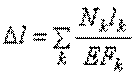 ,
,
где E – модуль Юнга, а 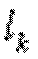 – длина соответствующего участка стержня.
– длина соответствующего участка стержня.
Тогда
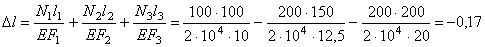 см.
см.
Таким образом, длина стержня уменьшается на 1,7 мм.
Вопросы для защиты.
1.Что такое прочность, жесткость, устойчивость?
2.В чем сущность метода сечений?
3.Что такое напряжение и в каких единицах измеряется?
4.Какие известны виды деформаций?
5.Какая деформация называется центральным растяжением (сжатием)?
6.Какие формулы, выражающие закон Гука, Вы знаете?
Задача 2. Расчет вала на прочность при кручении
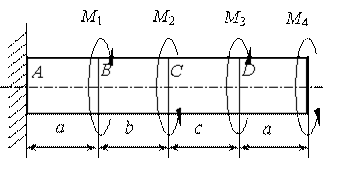
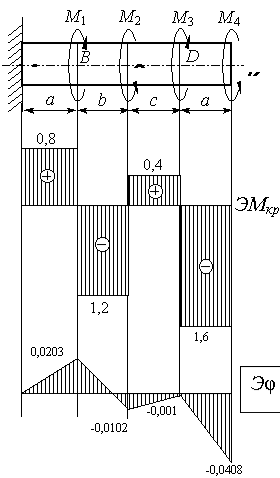
К стальному валу (см.рис.5.10) приложены скручивающие моменты: М1, M2, M3, M4. Требуется:
1) построить эпюру крутящих моментов;
2) при заданном значении 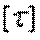 определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;
определить диаметр вала из расчета на прочность и округлить его величину до ближайшей большей, соответственно равной: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм;
3) построить эпюру углов закручивания;
4) найти наибольший относительный угол закручивания.
Дано: М1 = М3 = 2 кНм, М2 = М4 = 1,6 кНм, а = b = с = 1,2 м, 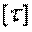 = 80 МПа.
= 80 МПа.
| № вар. | M1 | M2 | M3 | M4 | a | b | c |
| 1,0 | 2,9 | 2,0 | |||||
| 1,1 | 2,8 | 2,1 | |||||
| 1,2 | 2,7 | 2,2 | |||||
| 1,3 | 2,6 | 2,3 | |||||
| 1,4 | 2,5 | 2,4 | |||||
| 1,5 | 2,4 | 2,5 | |||||
| 1,6 | 2,3 | 2,6 | |||||
| 1,7 | 2,2 | 2,7 | |||||
| 1,8 | 2,1 | 2,8 | |||||
| 1,9 | 2,0 | 2,9 | |||||
| 2,0 | 1,9 | 3,1 | |||||
| 2,1 | 1,8 | 3,2 | |||||
| 2,2 | 1,7 | 3,3 | |||||
| 2,3 | 1,6 | 3,4 | |||||
| 2,4 | 1,5 | 3,5 | |||||
| 2,5 | 1,4 | 3,6 | |||||
| 2,6 | 1,3 | 3,7 | |||||
| 2` | 2,7 | 1,2 | 3,8 | ||||
| 2,8 | 1,1 | 3,9 | |||||
| 2,9 | 1,0 | 4,0 |
Решение.
1. Построить эпюру крутящих моментов.
При построений эпюр Мкр примем следующее правило знаков: крутящий момент считается положительным, если при взгляде в торец отсеченной части бруса действующий на него момент представляется направленным по движению часовой стрелки.
Крутящие моменты, возникающие в поперечных сечениях брусьев, определяются по внешним окручивающим моментам с помощью метода сечений. На основании метода сечения крутящий момент в произвольном поперечном сечении бруса численно равен алгебраической сумме внешних скручивающих моментов, приложенных к брусу по одну сторону от рассматриваемого сечения.
Для брусьев, имеющих один неподвижно закрепленный (заделанный) и один свободный конец, крутящие моменты всех поперечных сечений удобно выражать через внешние моменты, приложенные с той стороны от рассматриваемого сечения, с которой расположен свободный конец. Это позволяет определять крутящие моменты, не вычисляя реактивного момента, возникающего в заделке.
Для построения эпюры крутящих моментов необходимо найти величины крутящих моментов на каждом участке вала.
I участок (КД):
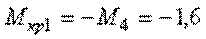 кНм,
кНм,
II участок (СД):
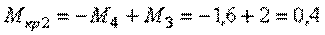 кНм,
кНм,
III участок (СВ):
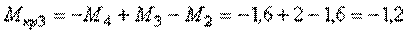 кНм,
кНм,
IV участок (ВА):
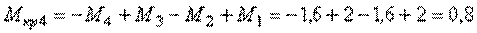 кНм.
кНм.
По значению этих моментов строим эпюру Мкр в выбранном масштабе. Положительные значения Мкр откладываем вверх, отрицательные - вниз от нулевой линии эпюры.
2. При заданном значении  определим диаметр вала из расчета на прочность.
определим диаметр вала из расчета на прочность.
Условие прочности при кручении имеет вид
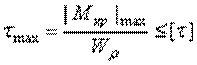 .
.
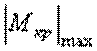 - максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры Мкр .
- максимальный крутящий момент, взятый по абсолютной величине. Определяется из эпюры Мкр .
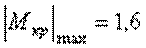 кНм;
кНм;
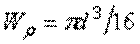 - полярный момент сопротивления для сплошного круглого вала.
- полярный момент сопротивления для сплошного круглого вала.
Диаметр вала определяется по формуле
 .
.
Принимаем d = 50 мм = 0,05 м.
3. Построим эпюру углов закручивания.
Угол закручивания участка вала длиной l постоянного поперечного сечения определяется по формуле
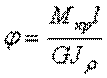 .
.
где  - жесткость сечения вала при кручении.
- жесткость сечения вала при кручении.
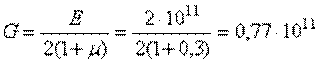 Н/м2;
Н/м2;
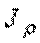 - полярный момент инерции круглого вала
- полярный момент инерции круглого вала
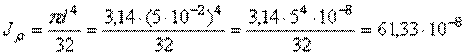 м4.
м4.
Вычислим углы закручивания сечений В, С, D и К относительно закрепленного конца вала (сечения А)
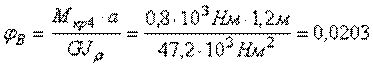 рад,
рад,
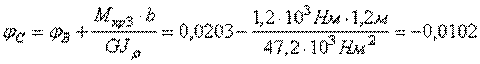 рад,
рад,
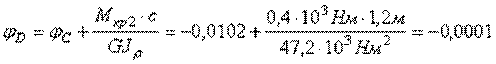 рад,
рад,
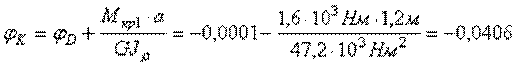 рад.
рад.
Строим эпюру углов закручивания.
4. Найдем наибольший относительный угол закручивания
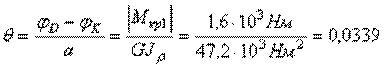 рад/м.
рад/м.
Вопросы для защиты.
1.Какие напряжения возникают в поперечных сечениях при кручении?
2.Что такое полярный момент сопротивления?
3.Напишите условие прочности при кручении.
4.Какая деформация возникает при кручении?
5.При какомнагружении возникает кручение?
