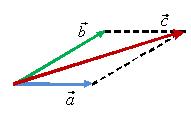
Два отличных от нуля вектора, которые находятся на одной прямой или параллельных прямых, называются коллинеарными векторами
Если два вектора a⃗ и b⃗ коллинеарны, то это записывается так: a⃗ ∥ b⃗
Два коллинеарных вектора могут быть направлены в одном направлении или в противоположных направлениях. В первом случае коллинеарные векторы называются сонаправленными, а во втором — противоположно направленными векторами
Сонаправленные векторы записываются a⃗ ↑↑b⃗ или b⃗ ↑↑a⃗;
противоположно направленные векторы записываются
a⃗ ↑↓b⃗ или b⃗ ↑↓a⃗ .
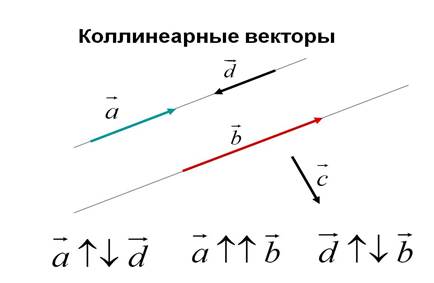
Векторы с равными модулями и одинаковыми направлениями называются равными векторами. ИЛИ Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны
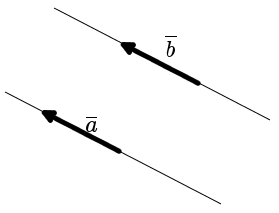
Равные векторы a⃗ и b⃗ записываются так: a⃗ = b⃗ или b⃗ = a⃗ .
Векторы с равными модулями и противоположными направлениями называются противоположными векторами.
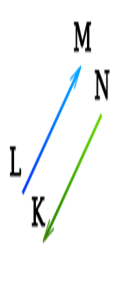
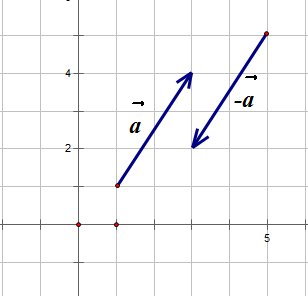
Противоположные векторы a⃗ и b⃗ записываются так: a⃗ = − b⃗ или b⃗ = − a⃗ .
Меняя направление какого-либо вектора на противоположное, получается вектор, противоположный данному.
Действия с векторами.
В школьном курсе геометрии рассматривается ряд действий и правил с векторами: сложение по правилу треугольника, сложение по правилу параллелограмма, сложение по правилу многоугольника, правило разности векторов, умножения вектора на число, скалярное произведение векторов и др.
Сложение векторов по правилу треугольников
Рассмотрим два произвольных ненулевых вектора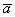 
и 
:
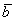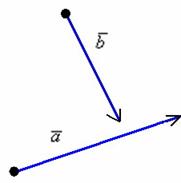
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор 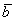от конца вектора :
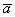Суммой векторов 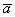и 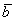является вектор 
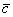. Для лучшего понимания правила в него целесообразно вложить физический смысл: пусть некоторое тело совершило путь по вектору 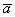, а затем по вектору 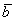. Тогда сумма векторов 
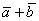представляет собой вектор результирующего пути 
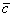с началом в точке отправления и концом в точке прибытия.
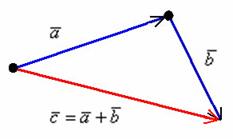
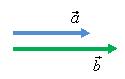
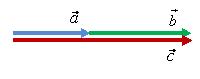
При помощи правила треугольника можно сложить два параллельных вектора a⃗ и b⃗ и a⃗ . Сумма этих векторов c⃗ =a⃗ +b⃗ изображены на рис..
Сложение векторов по правилу параллелограмма
Рассмотрим два произвольных ненулевых вектора 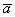и :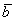
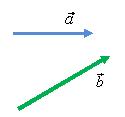
Для того чтобы сложить эти два вектора ) нужно переместить их параллельно самим себе так, чтобы начала векторов находились в одной точке
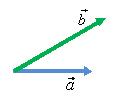
Затем построить параллелограмм, сторонами которого будут эти вектора
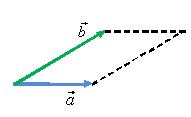
Тогда суммой a⃗ + b⃗ будет вектор c⃗ начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма
