Основные свойства операторных групп

Пример 2.3.1. Пусть А – подгруппа из нормализатора 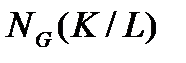секции 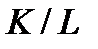группы G. Зададим действие А на 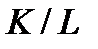сопряжением: 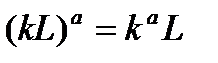для любого 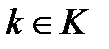и для любого 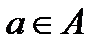. Тогда А – группа операторов группы 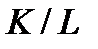, причем множество всех тождественных операторов из А совпадает с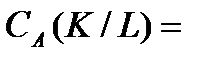

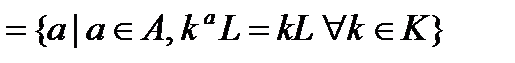. В частности, если 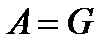, то G является группой операторов своей нормальной секции 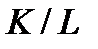, причем G действует тождественно на 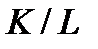тогда и только тогда, когда 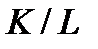центральна в G, т.е. .

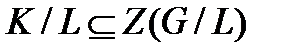В дальнейшем при рассмотрении действия подгрупп из G на секциях группы G без указания способа задания действия, будем иметь в виду действие, описанное в примере 2.2.1.

Определение 2.3.13. Пусть G и Н являются 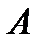- операторными группами. Группа G называется А-изоморфной группе Н, если существует изоморфное отображение 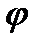группы G на Н такое, что 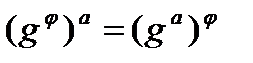для любого 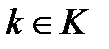и для любого .

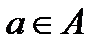Лемма 2.3.2. Пусть А-операторная группа G обладает А-композиционным (конечным) рядом длины 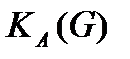и и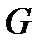меет нормальные А-допустимые подгруппы 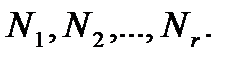Тогда каждый А-композиционный фактор группы 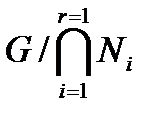А-изоморфен некоторому А-композиционному фактору хотя бы одной из групп 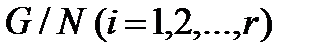и .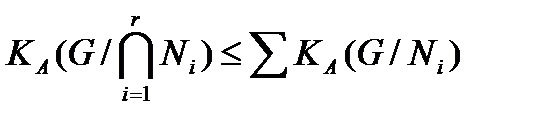

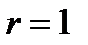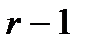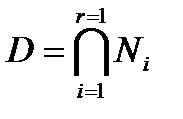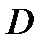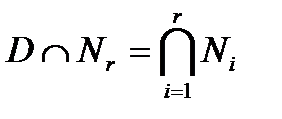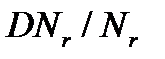Доказательство. При утверждение леммы верно. Допустим, что утверждение верно для нормальной в G А-допустимой подгруппы. Пусть . Тогда подгруппа нормальна в G и А-допустима. Далее, и А-допустима и нормальна в 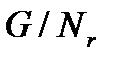. Так как группа 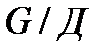А-изоморфна группе 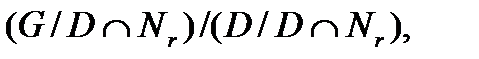то каждый А-композиционный фактор группы 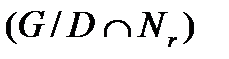А-изоморфен А-композиционно-

му фактору либо группы 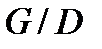и значит по предложению индукции некоторой группы 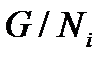, , 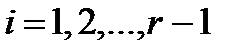либо группы 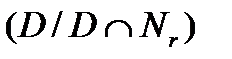А-изоморфной группе 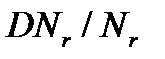и значит группы 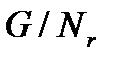, причем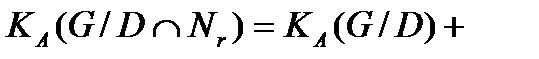 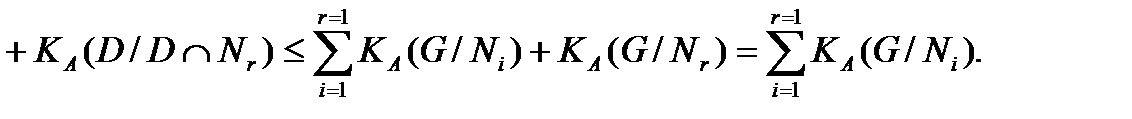Лемма доказана.

Следствие 2.3.2. Пусть группа G обладает главным (конечным) рядом и 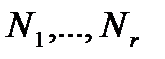– нормальные подгруппы группы G. Тогда каждый главный фактор группы 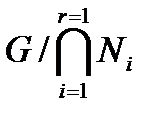G-изоморфен главному фактору хотя бы одной из групп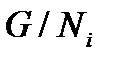 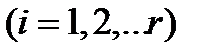и .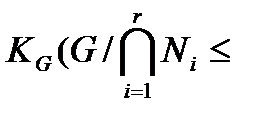

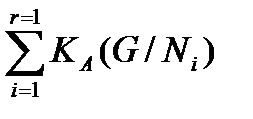Доказательство. Полагаем по лемме 2.3.2 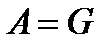. Тогда А-композиционный фактор групп G, 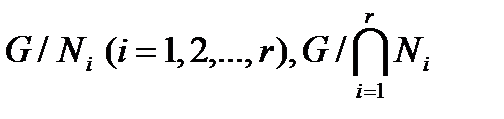является главным фактором этих групп. Следствие доказано.

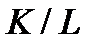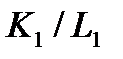Лемма 2.3.3. Пусть и – нормальные секции группы G. Есл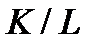и и 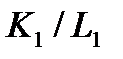G-изоморфны, то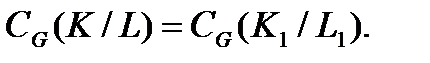

Доказательство. Пусть 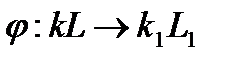является G-изоморфизмом 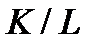и 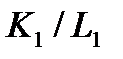. Тогда 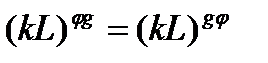для любого 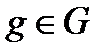и для любого 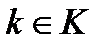. Следовательно, 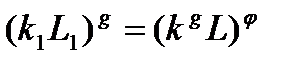. Пусть 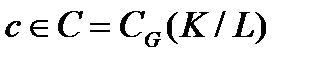. Тогда 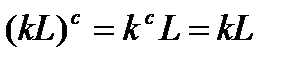для любого 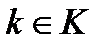. Поэтому 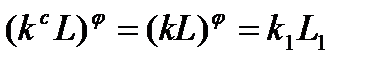, и значит, 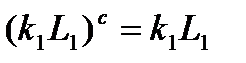для любого 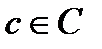. Так как 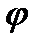является отображением 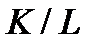на 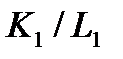, то когда 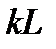пробегает группу 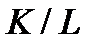, то 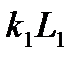пробегает группу 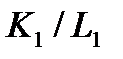. Следовательно, 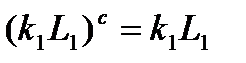для любого 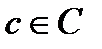и 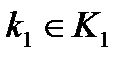. Поэтому 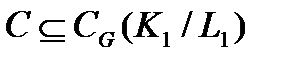. Рассматривая отображение 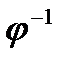, в силу симметрии, аналогично получим 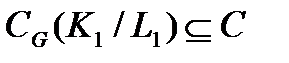. Следовательно, .

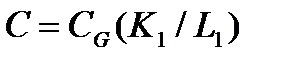Лемма 2.3.4. а) Если 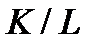– главный фактор конечной группы G и 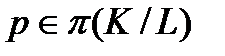, то 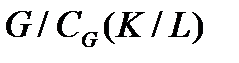не содержит неединичных нормальных р-подгрупп, причем, 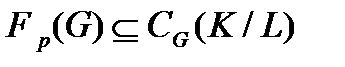,где 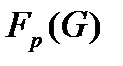– наибольшая нормальная р-нильпотентная подгруппа группы G;

б) если G – конечная А-операторная группа и 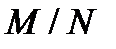– А-композиционный р-фактор группы G, то 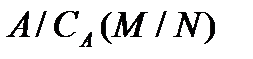не имеет неединичных нормальных р-подгрупп.

Доказательство. а) Пусть 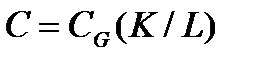и 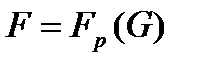. Тогда по следствию 2.3.1 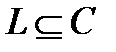и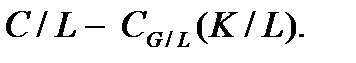

Пусть 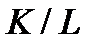является неабелевой 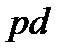-группой. Так как 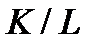является минимальной нормальной подгруппой группы 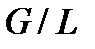, то 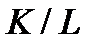является прямым произведением изоморфных неабелевых простых 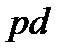-групп. Тогда 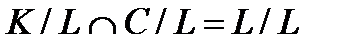, и значит, 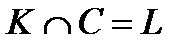. Далее 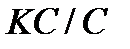G-изоморфен группе 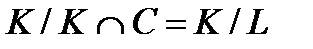. Тогда в группе 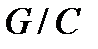подгруппа 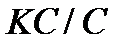является неабелевой минимальной нормальной 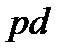-группой. По лемме 2.3.5 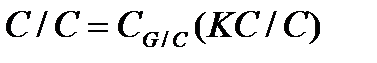. Следовательно, 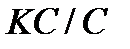имеет единичный централизатор в группе 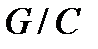. Отсюда следует, что 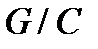не имеет неединичных нормальных 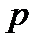-подгрупп и 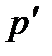-подгрупп. Поэтому 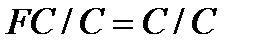, и значит, .

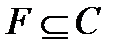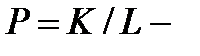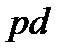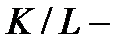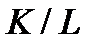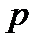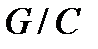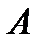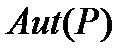Пусть теперь абелева -группа. Так как главный фактор группы G, то является элементарной абелевой -группой. По следствию 2.3.1 в) группа изоморфна некоторой подгруппе из . Так как 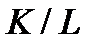является главным фактором группы G, то не существует 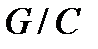-допустимой подгруппы 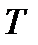в 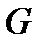такой, что 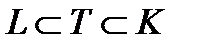, т.е. 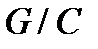действует на 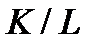неприводимо. Тогда в полупрямом произведении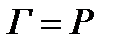 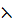А подгруппа 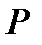является минимальной нормальной подгруппой. Допустим, что 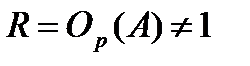. Тогда 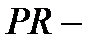нормальная 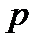-подгруппой группы 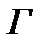. Так как 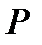нормальна в 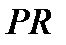, то 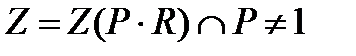. Так как 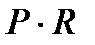нормальна в 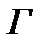и 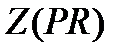характеристична в 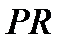, то 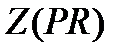нормальна в 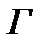. Тогда 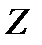нормальна в 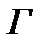как пересечение нормальных подгрупп из 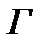. 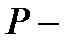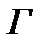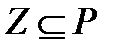Так как минимальная нормальная подгруппа в и , то 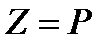. Следовательно, 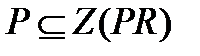. 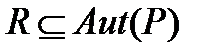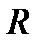Так как и централизует 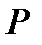, то 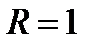. Получили противоречие. Значит, 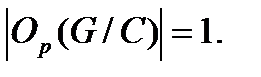Если 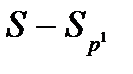-подгруппа из 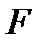, то 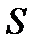характеристична в 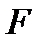, и значит, 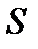нормальна в G. Рассмотрим группу 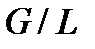. Тогда 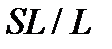и 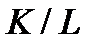являются нормальными подгруппами группы 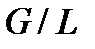, причем 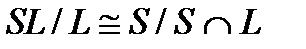является 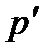-подгруппой, а 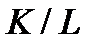элементарной абелевой 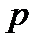-группой. Тогда 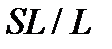и 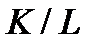поэлементно перестановочны. Значит, 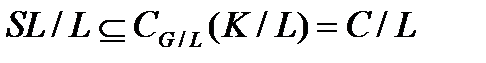. Следовательно, 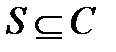. Поэтому 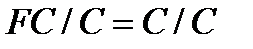, и значит, 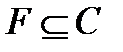. Утверждение а) доказано.

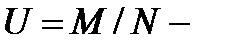
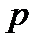б) Так как -композиционный -фактор группы G, то в М не существует 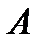-допустимой нормальной подгруппы 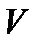такой, что 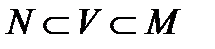. Тогда в полупрямом произведении 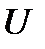подгруппа 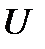является минимальной нормальной подгруппой и значит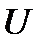 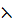A=X является элементарной абелевой 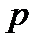-группой. По пункту а) 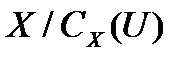не имеет неединичных нормальных 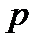-подгрупп. Так как 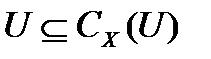, то 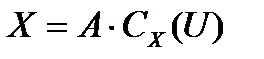. Тогда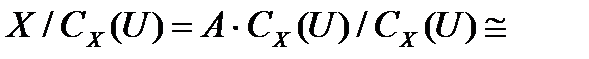 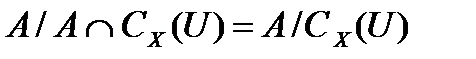, и значит, 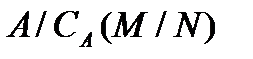не имеет неединичных нормальных 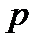-подгрупп. Лемма доказана.

Заключение

В реферате выполнены следующие задачи:

§ Рассмотрены основные определения теории групп (определение группы, подгруппы, нормальной подгруппы, правого и левого смежного классов, нормализатора, централизатора подмножества в группе и другие).

§ Проведено исследование основных понятий, связанных с операторными группами.

§ Изучены простейшие свойства нормализаторов и централизаторов секций конечной группы.

§ Изучены основные свойства операторных групп.

Список литературы

1. Ведерников В.А. Элементы теории классов групп. – Смоленск, 1988.

2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.

3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.

4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.

5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.

6. Кострикин А.И. Сборник задач по алгебре. - М.: Физико-математическая литература, 2001.

7. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.

8. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.

9. Скиба А.Н. Алгебра формаций. – Мн.: Беларуская навука, 1997.

10. Шеметков Л.А., Скиба А.Н. Формации алгебраических систем. – М.: Наука, 1989.

11. Шеметков. Л.А. Формации конечных групп. – М.: Наука, 1978.