Тема 5. Электрические модели типовых динамических звеньев
Каждое из рассмотренных нами динамических звеньев может быть представлено в виде электрического, механического или электромеханического аналогов, процессы в которых математически описываются соответствующим одним и тем же дифференциальным уравнением.
Рассмотрим электрические модели наиболее часто встречающихся типовых звеньев.
Апериодическое звено. Апериодическими звеньями являются RC и RL цепи, входные и выходные величины которых связаны соответствующей передаточной функцией.
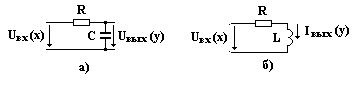
Для схемы а) напряжение на выходе в комплексном виде равно:
Uвых(jω) = I(jω)∙xc/j = I(jω)∙1/(jωC);
I(jω) = Uвх(jω)/[R + 1/(jωC)] = jωC∙ Uвх(jω)/(jωRC +1);
Uвых(jω) = Uвх(jω)/(jωRC +1). (1)
Представим уравнение (1) в операторной форме, заменив комплексную переменную jω на оператор Лапласа р:
Uвых(р) = Uвх(p)/(рRC +1) = Uвх(p)/(рТ +1). (2)
Как следует из уравнения (2), передаточная функция схемы а) соответствует передаточной функции типового апериодического звена:
W(p) = y/x = Uвых(р)/Uвх(p) = 1/(рТ +1), где (3)
коэффициент усиления К равен 1, а постоянная времени Т равна произведению RC.
Для схемы б) ток на выходе в комплексном виде равен:
Iвых(jω) = Uвх(jω)/(R + jxL) = Uвх(jω)/(R + jωL);
Iвых(jω) = Uвх(jω)∙(1/R)/[jω∙(L/R) +1)]. (4)
Заменяя в уравнении (4) комплексную переменную jω на оператор Лапласа р, получим уравнение схемы б) в операторной форме:
Iвых(р) = Uвх(р)∙(1/R)/[р∙(L/R) +1)] = Uвх(р)∙K/(рТ +1). (5)
Из выражения (5) следует, что передаточная функция данной схемы устанавливает связь между выходным током и входным напряжением:
W(p) = y/x = Iвых(р)/Uвх(p) = K/(рТ +1), где (6)
коэффициент усиления К равен 1/R, а постоянная времени Т равна отношению L/R.
,25моделировать апериодические звенья с требуемыми характеристиками.
Колебательное звено. Оно представляет собой последовательное соединение RLC элементов:
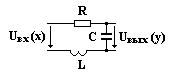
Представим напряжение на выходе колебательного звена сразу в операторной форме:
Uвых(р) = I(p)∙1/pC = Uвх(p)∙(1/pC)/[R + pL + (1/pC)] =
= Uвх(p)/(p2CL + pRC + 1) = Uвх(p)/(p2T2 + p2ξT + 1), (7)
где Т2 = CL; 2ξT = CR.
Тогда передаточная функция колебательного звена:
W(p) = y/x = Uвых(р)/Uвх(p) = 1/( p2T2 + p2ξT + 1), (8)
где коэффициент усиления равен К = 1.
Коэффициент демпфирования ξ можно найти из следующих соотношений:
T = √CL; 2ξ√CL = CR,
откуда ξ = CR/(2√CL) = 0,5∙R∙C/√(C∙L). (9)
Для случая отсутствия активных потерь в колебательном контуре (R = 0) имеем согласно выражению (9): ξ = 0, т.е. в контуре имеют место незатухающие колебания. Колебательное звено превращается в апериодическое звено второго порядка, когда ξ = 1, т.е. при условии, что 0,5∙R∙C = √(C∙L) или R2∙C = 4L.
Интегрирующее звено.
Идеальными интегрирующими звеньями являются цепи с элементами С и L. В схеме а) входной величиной х является ток заряда конденсатора, а напряжение на нем – выходной величиной у. В схеме б) входной величиной х является напряжение на индуктивности, а ток – выходной величиной у.
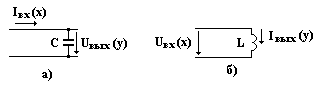
Представим напряжение на выходе схемы а) в операторной форме:
Uвых(р) = Iвх(р)∙1/(рС). (10)
Следовательно, передаточная функция данного звена равна:
W(p) = y/x = Uвых(р)/Iвх(p) = (1/C)/p = К/р, (11)
где К = 1/С.
Отличительным свойством интегрирующего звена является то, что после прекращения действия входного сигнала выходной сигнал звена остается на том уровне, на котором был в момент исчезновения входного сигнала. Иначе говоря, интегрирующее звено обладает свойством «запоминать» последнее значение выходной величины, благодаря чему достигается астатизм автоматической системы. Другой особенностью интегрирующего звена является то, что скорость изменения выходной величины у прямопропорциональна значению входной величины х.
В операторной форме уравнение интегрирующего звена по схеме б):
Iвых(р) = Uвх(р)/(рL). (12)
Соответственно, передаточная функция звена равна:
W(p) = y/x = Iвых(р)/Uвх(p) = (1/L)/p = К/р, (13)
где К = 1/L.
Дифференцирующее звено. Идеальными дифференцирующими звеньями являются цепи с конденсатором и элементом индуктивности. Входной величиной х в схеме а) является напряжение, а ток через конденсатор - выходной величиной у. В схеме б) входной величиной х является входной ток, а напряжение на индуктивности – выходной величиной у.
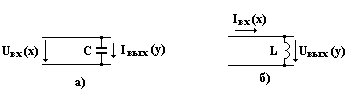
Представим выходной ток схемы а) в операторной форме:
Iвых(р) = Uвх(р)∙рС. (14)
Соответственно, передаточная функция данного звена равна:
W(p) = y/x = Iвых(р)/Uвх(p) = pC = Кр, (15)
где К = С.
Особенностью дифференцирующего звена является то, что значение выходной величины у прямопропорциональна скорости изменения входной величины х.
В операторной форме уравнение дифференцирующего звена по схеме б):
Uвых(р) = Iвх(р)∙рL. (16)
Соответственно, передаточная функция звена равна:
W(p) = y/x = Uвых(р)/Iвх(p) = pL = К∙р, (17)
где К = L.
