Математическое описание звена. Форсирующее звено I-ого порядка описывается уравнением:

Форсирующее звено I-ого порядка описывается уравнением:

у(t) = K·[T·dх(t)/dt + х(t)]

Как и в случае с дифференцирующим звеном, здесь мы имеем дело не с дифференциальным, а с обычным алгебраическим уравнением, поскольку входной сигнал х(t) и его производные полагаются заранее известными.

Физическая реализация звена.

Подчеркнем, что форсирующие звенья также как и дифференцирующее звено являются физически нереализуемым. На практика их можно более-менее удовлетворительно представить с помощью комбинации, например, идеального форсирующего и апериодического звена.

Переходная функция.

h(t) = L^-1[W(s)/s] = K·1(t) + K·T·δ(t)

Весовая функция.

w(t) = L^-1[W(s)] = K·δ(t) + K·T·dδ(t)/dt

Рассмотрим отклик форсирующего звена I-ого порядка на линейное (нарастающее) входное воздействие:

х(t) = t Х(s) = 1/s².

у(t) = L^-1[W(s)·Х(s)] = L^-1[K·(T·s + 1)/s²] = L^-1[K·T/s + K/s²] = K·T·1(t) + K·t.

Другими словами, если на вход форсирующего звена I-ого порядка подать линейно нарастающий сигнал, то в момент подачи сигнала на выходе мы будем иметь скачок выходного сигнала с 0 до KT, а затем выходной сигнал будет линейно нарастать, т.е. повторять с некоторым коэффициентом усиления входной сигнал. Можно сказать, что это звено, как бы опережает (форсирует) входной сигнал. Отсюда и его название.

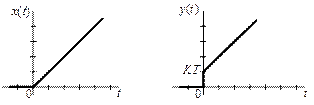
Частотные характеристики.

АФЧХ, АЧХ, ФЧХ и ЛАХ форсирующего звена I-ого порядка имеют вид:

W(jω) = K + KTω·j

A(ω)= 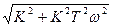=K·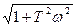

φ(ω) = arctg(KTω/K) = arctg(Tω)

L(ω) = 20lgK + 10lg(1+T²ω²)

Как видим, частотные характеристики форсирующего звена I-ого порядка обратны частотным характеристикам апериодического звена I-ого порядка.

Форсирующее звено II-ого порядка

Передаточная функция.

Передаточная функция форсирующего звена II-ого порядка имеет вид:

W(s) = K·(T₁²s² + T₂s + 1) где K – коэффициент усиления; T₁ и T₂ – постоянные времени.

Математическое описание звена.

Форсирующее звено II-ого порядка описывается уравнением:

у(t) = K·[T₁²·d²х(t)/dt² + T₂·dх(t)/dt + х(t)]

Как и в случае с дифференцирующим звеном, здесь мы имеем дело не с дифференциальным, а с обычным алгебраическим уравнением, поскольку входной сигнал y(t) и его производные полагаются заранее известными.

Переходная функция.

h(t) = L^-1[W(s)/s] = K·1(t) + K·T₂·δ(t) + K·T₁²·dδ(t)/dt

Весовая функция.

w(t) = L^-1[W(s)] = K·δ(t) + K·T₂·dδ(t)/dt + K·T₁²·d²δ(t)/dt²

Рассмотрим отклик форсирующего звена II-ого порядка на параболически нарастающее входное воздействие:

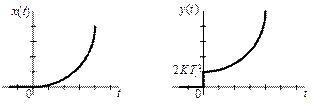
х(t) = t² Х(s) = 2/s³.

у(t) = L^-1[W(s)·Х(s)] = L^-1[2K·(T₁²·s² + T₂s + 1)/s³] = 2K·T₁²·1(t) + 2K·T₂·t + Kt²

Другими словами, если на вход форсирующего звена II-ого порядка подать параболически нарастающий сигнал, то в момент подачи сигнала на выходе мы будем иметь скачок выходного сигнала с 0 до 2KT₁², а затем выходной сигнал будет нарастать по параболическому закону, т.е. в общих чертах повторять входной сигнал. Здесь, как и в случае форсирующего звена I-ого порядка, можно сказать, что это звено, как бы опережает (форсирует) входной сигнал.

Частотные характеристики.

Мы не будем здесь рассматривать частотные характеристики форсирующего звена II-ого порядка, т.к. они имеют достаточно сложный вид. Скажем только, что, как и в случае форсирующего звена I-ого порядка, они обратны частотным характеристикам либо апериодического звена II-ого порядка, либо колебательного звена, в зависимости от соотношения временных параметров T₁ и T₂.

Звено с чистым запаздыванием

Звено с чистым запаздыванием – это такое звено, у которого выходной сигнал полностью повторяет входной сигнал с некоторой задержкой во времени.

Передаточная функция.

Передаточная функция звена с чистым запаздыванием имеет вид:

W(s) = e^{-τ s} где τ – время чистого запаздывания.