Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю
Достаточность этих условий вытекает из того, что при FО=0 система сходящихся сил, приложенных в центре приведения О, эквивалентна нулю, а при МО=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю.
Докажем необходимость этих условий. Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что в нашем случае система сил Qи Р должна быть эквивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и, кроме того, должно выполняться равенство Q= –Р. Но в рассматриваемом нами случае это может быть, если линия действия силы Р проходит через точку О, т.е. если h=0. А это означает, что главный момент равен нулю (МО=0). Далее, так как Q+Р=0, а Q = FО+Р', то FО+Р'+Р=0, и следовательно, FО=0.
Итак, необходимые и достаточные условия равновесия пространственной системы сил будут иметь вид
FО=0, МО =0 (4.15) или в проекциях на координатные оси,
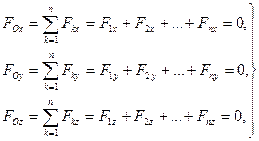 (4.16)
(4.16)
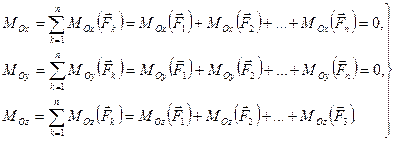 (4.17)
(4.17)
Таким образом, при решении задач о равновесии пространственной системы сил, приложенных к твердому телу, мы имеем возможность из уравнений (4.16) и (4.17) определить шесть неизвестных величин.
Замечание. О невозможности приведения пары сил к равнодействующей.Проведем доказательство от противного. Пусть пара сил (F1,F'1) приводится к равнодействующей R, приложенной к какой-либо точке А тела. Тогда эта сила и силаR'(R'= – R), приложенная к точке А, эквивалентны нулю. На основании только что 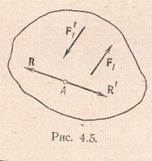 доказанного главный вектор и главный момент этой системы должны быть равны нулю. Примем за центр приведения точку А, тогда главный момент МА≠0 и равен моменту пары (F1,F'1); главный вектор тоже не равен нулю (FА=R'≠0). Следовательно, предположение о существовании равнодействующей для пары сил несправедливо.
доказанного главный вектор и главный момент этой системы должны быть равны нулю. Примем за центр приведения точку А, тогда главный момент МА≠0 и равен моменту пары (F1,F'1); главный вектор тоже не равен нулю (FА=R'≠0). Следовательно, предположение о существовании равнодействующей для пары сил несправедливо.
Уравнения равновесия для более частных систем сил могут быть получены из уравнений (4.16) и (4.17).
1. Равновесие пространственной системы параллельных сил.
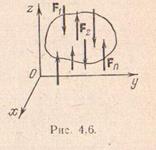 Направим ось z параллельно линиям действия сил. Тогда проекция сил Fk на оси х и у равны нулю (Fkх≡0, Fkу≡0) и остается удовлетворить только одному из уравнений группы (4.16):
Направим ось z параллельно линиям действия сил. Тогда проекция сил Fk на оси х и у равны нулю (Fkх≡0, Fkу≡0) и остается удовлетворить только одному из уравнений группы (4.16):
FОz=ΣFkz=F1z +F2z+ … + Fпz=0. (4.18)
Во второй группе уравнений (4.17) последнее выполняется тождественно, так как силы параллельны оси z (МОz(Fk)≡0), и остаются только уравнения:
МОх =∑МОх(Fk)=МОх(F1)+ МОх(F2)+ … + МОх(Fп)=0, (4.19)
МОу =∑МОу(Fk)=МОу(F1)+ МОу(F2)+ … + МОу(Fп)=0.
2. Равновесие плоской системы сил.
Для плоской системы сил из уравнений первой группы останутся два уравнения:
FОх=ΣFkх=F1х+F2х+ … + Fпх=0,
FОz=ΣFkz=F1z +F2z+ … + Fпz=0. (4.20)
Из уравнений второй группы два первых удовлетворяются тождественно, так как силы лежат в одной плоскости с осями х и у. Остается только третье уравнение:
МОz =∑МОz(Fk)=МОz(F1)+ МОz(F2)+ … + МОz(Fп)=0. (4.21)
3. Равновесие плоской системы параллельных сил.
Условие равновесия для этого частного случая следует из уравнений (4.20) и (4.21). Направим ось у параллельно линиям действия сил.
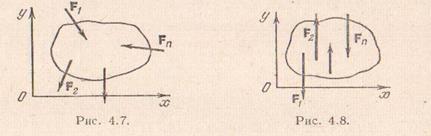
Тогда первое из уравнений (4.20) удовлетворяется тождественно (для любой системы параллельных сил на плоскости) и остаются только два уравнения равновесия:
FОу=∑Fkу=F1у +F2у+ … + Fпу=0,
МОz= ∑МОz(Fk)=МОz(F1)+ МОz(F2)+ … + МОz(Fп)=0. (4.22)
Напомним, что при составлении уравнений равновесия за центр приведения может быть выбрана любая точка.
Глава 5. Плоская система сил
