Модели краткосрочного страхования жизни
В актуарной математике модели страхования жизни условно делят на две большие группы в зависимости от того, принимается или нет в расчет доход от инвестирования собранных премий. Если нет, то мы говорим о краткосрочном страховании; обычно в качестве такого «короткого» интервала мы будем рассматривать интервал в 1 год. Если же да, то мы говорим о долгосрочном страховании. Конечно, это деление условное и, кроме того, долгосрочное страхование связано с рядом других обстоятельств.
Анализ индивидуальных убытков при краткосрочном
Страховании жизни
Простейший вид страхования жизни заключается в следующем. Страхователь платит страховой компании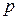 
рублей (эта сумма называется страховой премией), а компания обязуется выплатить лицу, в пользу которого заключен договор, страховую сумму 
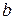рублей в случае смерти застрахованного в течение года по причинам, перечисленным в договоре (и не платит ничего, если он не умрет в течение года или умрет по причине, которая не покрывается договором). Страхователем может быть сам застрахованный или другое лицо (например, его работодатель).
Величина страховой выплаты, конечно, много больше, чем страховая премия: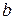 
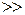
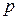, и нахождение «правильного» соотношения между ними – одна из важнейших задач актуарной математики.
Купив за 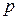руб. страховой полис, страхователь избавил выгодоприобретателя от риска финансовых потерь, связанных с неопределенностью момента смерти застрахованного. Этот риск приняла на себя страховая компания. Для страховой компании риск заключается в случайности убытка по рассматриваемому договору; если застрахованный не умирает в течение года, то убыток равен 0; если же не умирает, то убыток равен 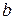руб. Этот индивидуальный убыток является элементарный составляющей финансового риска компании и поэтому изучение финансовой деятельности компании начинается с изучения индивидуальных убытков.
Прежде всего мы отмечаем, что индивидуальный убыток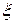 
является случайной величиной. Поэтому важнейший элемент его анализа – это определение распределения этой случайной величины. В рассматриваемой нами простейшей схеме страхования распределение величины 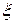имеет вид:
,
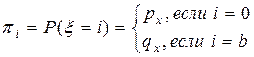где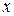 
- возраст застрахованного, 
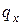- вероятность того, что человек в возрасте 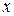лет, умрет в течение ближайшего года по причине, покрываемой договором, 
.
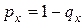Средняя величина убытка есть
,
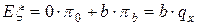а дисперсия
.
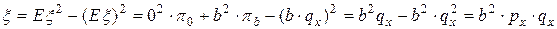Наряду с величиной 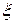, описывающей индивидуальный убыток, мы введем новую случайную величину 
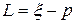, которая описывает потери компании от заключенного договора страхования. Она принимает два значения: 
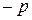и 
с вероятностям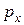и 
и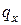 
соответственно. Таким образом, с вероятностью 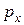компания имеет доход 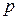рублей, а с вероятностью 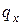терпит потери, равные 
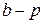рублей.
Средние потери компании равны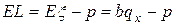 
. Эта формула позволяет получить простейшие выводы о величине страховой премии. Ясно, что средние потери компании должны быть неотрицательными, т.е. 
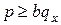. Минимально возможное значение 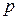равно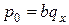 
. Оно соответствует нулевым средним потерям компании и называется нетто-премией. На самом деле реальная плата за страховку (брутто-премия или офисная премия) больше нетто-премии. Разница между ними (нагрузка) позволяет страховой компании покрыть административные расходы, обеспечить доход и, что самое главное, гарантировать малую вероятность разорения компании. Подробнее мы будем обсуждать этот вопрос позже, однако уже сейчас отметим, что неразорение компании означает просто выполнение своих обязательств перед клиентами, и в этом смысле разумное увеличение платы за страховку в интересах самих клиентов.
Страховая сумма часто принимается равной 1 или 1000. Это означает, что премия выражается как доля от страховой суммы или на 1000 страховой суммы соответственно.