Решение нелинейных уравнений

Метод хорд

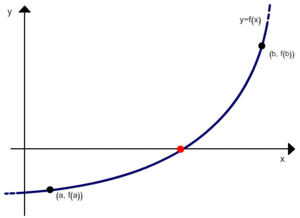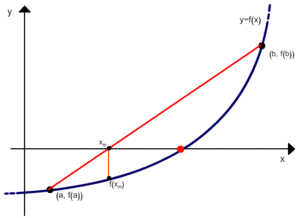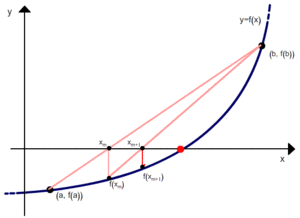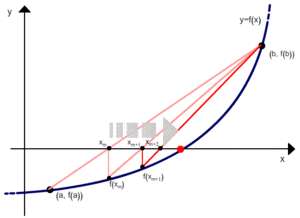
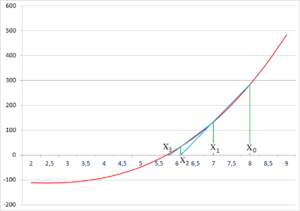
Первые три итерации метода хорд. Синим нарисована функция f(x), красными проводятся хорды.

Метод хорд — итерационный численный метод приближённого нахождения корня алгебраического уравнения.

Содержание [убрать] 1 Геометрическое описание 2 Алгебраическое описание метода 3 Пример использования 4 Критерий сходимости 5 Историческая справка 6 Пример кода 7 См. также 8 Литература 9 Примечания 10 Ссылки

Геометрическое описание

Будем искать корень функции f(x). Выберем две начальные точк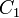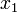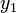и ( ; ) и 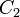( 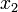; 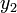) и проведем через них прямую. Она пересечет ось абсцисс в точке ( 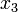;0). Теперь найдем значение функции с абсциссой 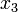. Временно будем считать 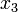корнем на отрезке [ 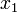; 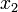]. Пусть точка 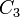имеет абсцисcу 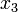и лежит на графике. Теперь вместо точек 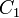и 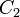мы возьмём точку 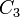и точку 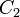. 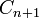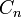Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки и и повторять операцию с ними. Отрезок, соединяющий последние 2 точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.

Алгебраическое описание метода

Пусть 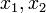− абсциссы концов хорды, 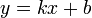− уравнение прямой, содержащей хорду. Найдем коэффициенты 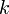и 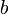из системы уравнений:

.

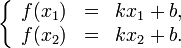Вычтем из первого уравнения второе:

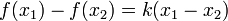, затем найдем коэффициенты 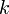и :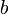

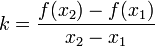, тогда

.

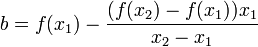Уравнение принимает вид:

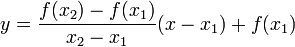
Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд:

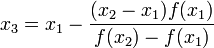
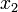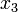Теперь возьмем координаты и и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока 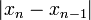не станет меньше или равно заданному значению погрешности.

Пример использования

Решим уравнение 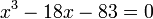методом хорд. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближени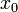й и 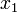концы отрезка, на котором отделён корень: 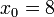и 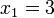. Вычисления ведутся до тех пор, пока не выполнится неравенство .

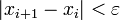Итерационная формула метода хорд имеет вид .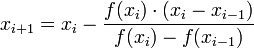

По этой формуле последовательно получаем (подчёркнуты верные значащие цифры):

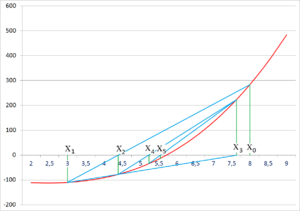
Первый случай

;

;

;

;

;

;

;

;

;

;

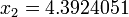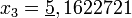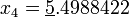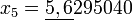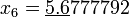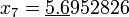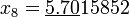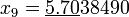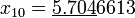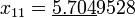Проверим, что метод работает и в том случае, есл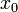и и 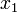выбраны по одну и ту же сторону от корня (то есть, если корень не отделён на отрезке между начальными приближениями). Возьмём для того же уравнения 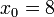и 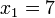. Тогда:

Второй случай

;

;

;

;

;

;

;

;

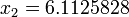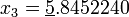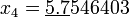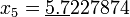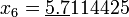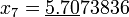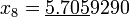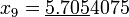Мы получили то же значение корня, причём за то же число итераций.

Критерий сходимости

Если 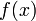дважды непрерывно дифференцируемая функция и знак 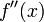сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно. Если корень 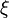уравнения 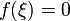находится на отрезке 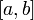, производные 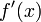и 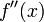на этом промежутке непрерывны и сохраняют постоянные знаки и 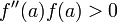, то можно доказать^[1], что погрешность приближенного решения стремится к нулю при n→∞, то есть метод сходится и сходится со скоростью геометрической прогрессии (при этом говорят, что он имеет линейную скорость сходимости^{[источник не указан 279 дней]}).

Решение нелинейных уравнений

Метод половинного деления ~ Метод хорд

Нелинейные уравнения можно разделить на 2 класса - алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.

Методы решения нелинейных уравнений делятся на две группы:

1. точные методы;
2. итерационные методы.

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Для их решения используются итерационные методы с заданной степенью точности.

Пусть дано уравнение

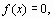(1)

где:

1. Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.
2. Значения f(x) на концах отрезка имеют разные знаки (f(a) * f(b) < 0).
3. Первая и вторая производные f' (x) и f'' (x) сохраняют определенный знак на всем отрезке.

Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.

Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.

Всякое значение 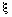, обращающее функцию f(x) в нуль, т.е. такое, что:

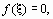называется корнем уравнения (1) или нулем функции f(x).

Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:

1. отделение корней - отыскание приближенного значения корня или содержащего его отрезка;
2. уточнение приближенных корней - доведение их до заданной степени точности.

Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.

Пример 1. Отделить корни уравнения:

f(x)º x3 - 6х + 2 = 0.

(2)

Составим приблизительную схему:

х	- ¥	- 3	- 1				+ ¥
f(x)	-	-	+	+	-	+	+

Следовательно, уравнение (2) имеет три действительных корня, лежащих в интервалах [-3, -1], [0, 1] и [1, 3].

Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.

В инженерной практике распространен графический способ определения приближенных корней.

Принимая во внимание, что действительные корни уравнения (1) - это точки пересечения графика функции f(x) с осью абсцисс, достаточно построить график функции f(x) и отметить точки пересечения f(x)с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением:

,

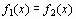(3)

где функции f₁(x) и f₂(x) - более простые, чем функция f(x). Тогда, построив графики функций у = f₁(x) и у = f₂(x), искомые корни получим как абсциссы точек пересечения этих графиков.

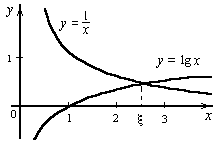
Рисунок 2.

Пример 2. Графически отделить корни уравнения (Рисунок 2):

x lg x = 1.

(4)

Уравнение (4) удобно переписать в виде равенства:

lg x= .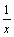

Отсюда ясно, что корни уравнения (4) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y = 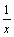. Построив эти кривые, приближенно найдем единственный корень 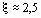уравнения (4) или определим его содержащий отрезок [2, 3].

Итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_n. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.