Определение 6. Множество из С называется областью, если открыто и связно.

Отметим, простой и понятный с виду факт, доказательство которого достаточно непросто.

Теорема 1 (Жордана). Любая жорданова криваяg разбивает плоскость 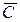на две непересекающиеся области, общей границей которых она является. При этом одна из областей, называемая внутренностью g, ограничена, а другая, называемая внешностью g и содержащая бесконечно удаленную точку, не ограничена .

Символ 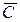мы сейчас поясним. В комплексном анализе нет понятия 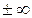, т.к. комплексные числа не сравнимы. Но пополнению комплексных чисел бесконечно удаленной точкой можно придать естественный геометрический вид.

Множество 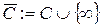называют расширенной комплексной плоскостью. Для наглядного изображения расширенной комплексной плоскости проведем специальное геометрическое построение.

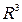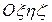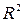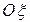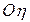Введем в пространстве систему координат так, чтобы плоскость С совпала с плоскостью и чтобы оси и совпали с осям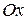и и 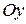комплексной плоскости z. Построим сферу S радиуса 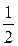с центром в точке 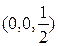, которая касается комплексной плоскости в начале координат.

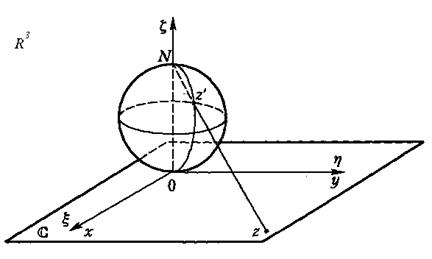
Рис.4

Точки 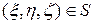удовлетворяет уравнению

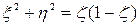
Точку 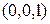обозначим через N и будем соединять ее с различными точками сферы 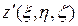прямолинейными лучами с началом в N и отмечать на каждом луче точку встречи его с плоскостью С. Тогда все точки сферы, за исключением точки N, спроектируются на плоскость С. Этим установлено взаимно-однозначное соответствие 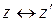между множествами С и 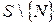. Если условимся, что 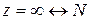, то получим взаимно одзначное соответствие между множествами 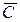и S. Это соответствие называется стереографической проекцией. Сферу S при этом называют сферой Римана.

Установим связь между координатами точке 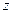и 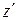. Координаты точки 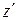удовлетворяют уравнению сферы, а условие, что точки N, 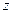и 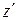лежат на одной прямой, имеет вид

.

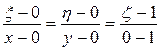Следовательно,

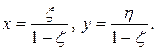
Принимая во внимание уравнение сферы и последнее равенство, имеем

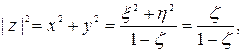
откуда

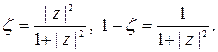
Теперь можно выразить переменные 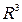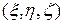, лежащие на сфере, через соответствующие точки плоскости , через x, y, z :

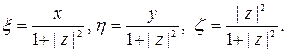
Получились «обратные» формулы, вместе с «прямыми» они называются основными формулами стереографической проекции.

Отметим два важных свойства стереографической проекции

Теорема 2. Стереографическая проекция обладает свойствами:

1)при стереографической проекции окружности всегда переходят в окружности ( при этом прямая на плоскости С считается окружностью бесконечного радиуса);

2)если две кривые на сфере S пересекаются в точке М, а касательные к этим кривым в точке М образуют угол a, то и угол между касательными к стереографической проекции этих кривых в точке 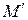их пересечения также равен a, т.е. величины углов при стереографической проекции сохраняются .

Для большей наглядности изложенного выше воспользуемся географической терминологией. Плоскость, проходящая через центр сферы параллельно плоскости 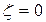, называется экваториальной. Согласно принятой терминологии, точка 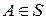лежит на параллели с широтой j, если радиус-вектор 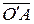с началом в центре сферы S образует угол j с экваториальной плоскостью, причем в верхней по отношению к этой плоскости части сферы j изменяется от 0 до 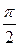, а в нижней части сферы – от 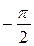до 0. Точки сферы, имеющие одну и туже широту j, образуют параллель данной широты. Долготой точки 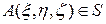называют 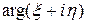. Совокупность точек данной долготы l образует полумеридиан этой долготы. Точка N называется северным полюсом, а начало координат 0 – южным полюсом.

Перейдем к рассмотрению примеров.

Пример 2.1. Найти на сфере Римана образы а) точки 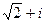, б) области .

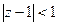Решение. а) точка 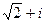имеет координаты 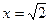, 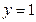. Тогда координаты точки образа на сфере Римана будут:

, , .

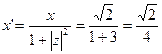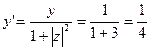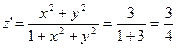б) уравнение области 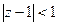на плоскости xОy будет иметь вид:

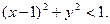
Или раскрывая скобки и преобразовывая:

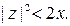
В силу основных формул стереографической проекции :

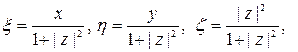
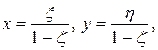
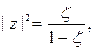
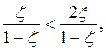
Т.к. знаменатель всегда положителен, для конечных точек плоскости, то

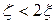– уравнение в совокупности с уравнением сферы и будет уравнением участка сферы Римана, на который отображается данная область.

Пример 2.2. Выяснить геометрический смысл:

а) 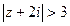, б) , .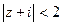

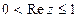Решение. а) данная область представляет собой все точки плоскости, за исключением круга с центром в точке (0, -2) и радиусом 3. (Рис.5).

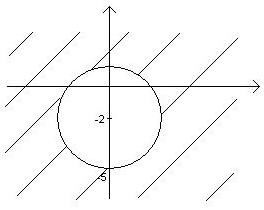
Рис.5

б) область, изображенная на рис. 6.

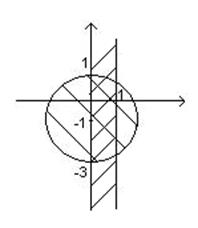
Рис.6

Пример 2.3. Какие кривые определяются следующими уравнениями (указать множество точек плоскости и порядок их похождения); представить кривые графически:

а) 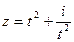; 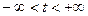, б) построить кривую .

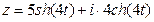Решение . а). Представим число z в ви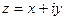де , где , .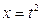

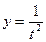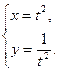
Решаем систему:

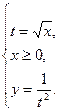
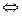
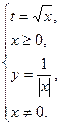
Таким образом, кривая – это ветвь гиперболы, лежащая в области x>0, y>0. см Рис. 7.

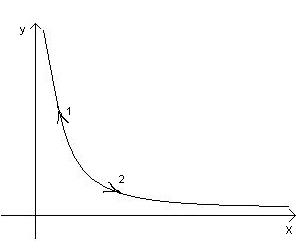
Рис.7

При 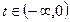обход происходит в направлении 1, при 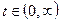– в направлении 2.

б) строим кривую .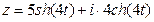

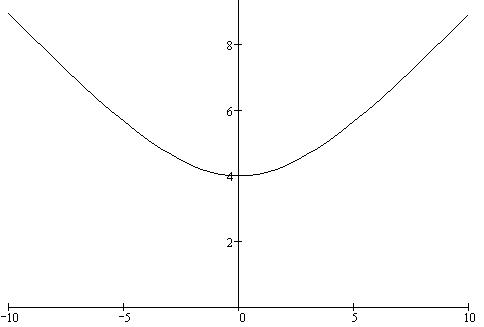
Рис.8