Частные случаи матриц
Государственное автономное профессиональное образовательное учреждение Свердловской области
«Сергинский многопрофильный техникум»
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Методические указания и индивидуальные задания к контрольной работе
для студентов заочного отделения
специальность: 230401 Информационные системы (по отраслям)
Верхние Серги
Методические указания и индивидуальные задания к контрольным работам / Сост. Соколова М.Г.; Сергинский многопрофильный техникум — Верхние Серги: ГАПОУ СО «Сергинский многопрофильный техникум», 2015.
Материал содержит краткие теоретические сведения, решения типовых примеров, индивидуальные задания.
Для студентов заочного отделения специальности:
230401 «Информационные системы» (по отраслям) по дисциплине "Элементы высшей математики".
В методической разработке содержатся задания по дисциплине «Элементы высшей математики», составленные в соответствии с программой по математике для студентов заочного отделения специальности 230401 Информационные системы (по отраслям)
Задания, входящие в методическую разработку могут быть использованы на практических занятиях, при проведении самостоятельных и контрольных работ, а также зачетов и экзаменов по данному курсу.
Часть 1
Основы линейной алгебры
И аналитическая геометрия
Методические указания и индивидуальные задания
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
И РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
1. Матрицы
1.1. Основные определения
Определение. Таблица чисел 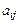 размерности m
размерности m 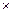 n называется матрицей, где m – число строк, n – число столбцов.
n называется матрицей, где m – число строк, n – число столбцов.
Матрица обозначается :
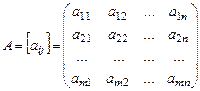 ,
,
где 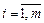 , а
, а 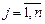 . Числа
. Числа 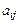 называются элементами матрицы.
называются элементами матрицы.
Определение.Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.
Определение. Суммой двух матриц А и В размерности m 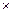 n называется такая матрица С размерности m
n называется такая матрица С размерности m 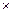 n, все элементы которой образованы по следующему закону :
n, все элементы которой образованы по следующему закону :
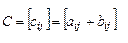 ,
,
где 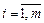 , а
, а 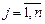 .
.
Определение. Произведением матрицы А размерности m 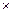 n на матрицу В размерности n
n на матрицу В размерности n 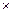 k называется такая матрица С размерности m
k называется такая матрица С размерности m 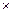 k, все элементы которой образованы по следующему закону :
k, все элементы которой образованы по следующему закону :
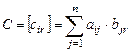 ,
,
где 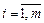 ,
, 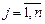 , а
, а 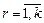 .
.
Частные случаи матриц.
1. Если 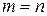 , то матрица называется квадратной. Её диагональ
, то матрица называется квадратной. Её диагональ 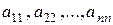 называется главной диагональю, а
называется главной диагональю, а 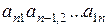 – побочная диагональ.
– побочная диагональ.
2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е. 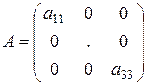 .
.
3. Диагональная матрица вида 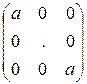 называется скалярной.
называется скалярной.
4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается 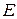 или
или 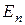 ,
, 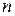 – порядок.
– порядок.
5. Матрица размера 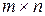 , у которой все элементы равны нулю, называется нулевой и обозначается
, у которой все элементы равны нулю, называется нулевой и обозначается 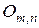 .
.
6. Если 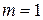 , то матрица называется строкой, или матрица-строка, или строка. Если
, то матрица называется строкой, или матрица-строка, или строка. Если 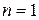
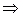 столбцовая = матрица-столбец = столбец.
столбцовая = матрица-столбец = столбец.
