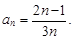Числовые последовательности

Рассмотрим ряд натуральных чисел: 1, 2, 3, ¼, n – 1, n, ¼ .

Если заменить каждое натуральное число n в этом ряду некоторым числом a_n, следуя некоторому закону, то получим новый ряд чисел:

a₁, a₂, a₃, ¼, a_n–1, a_n, ¼,

кратко обозначаемый 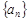и называемый числовой последователь-
ностью. Величина a_n называется общим членом числовой последовательности. Обычно числовая последовательность задается некоторой формулой a_n = f(n) позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задается путем описания ее членов.

По определению, последовательность всегда содержит бесконечное множество элементов: любые два разных ее элемента отличаются, по крайней мере, своими номерами, которых бесконечно много.

Числовая последовательность является частным случаем функции. Последовательность является функцией, определенной на множестве натуральных чисел и принимающей значения в множестве действительных чисел, т. е. функцией вида f : N ® R.

Последовательность 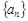называется возрастающей (убывающей), если для любого n Î N 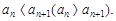Такие последовательности называются строго монотонными.

Иногда в качестве номеров удобно использовать не все натуральные числа, а лишь некоторые из них (например, натуральные числа, начиная с некоторого натурального числа n₀). Для нумерации также возможно использование не только натуральных, но и других чисел, например, n = 0, 1, 2, ¼ (здесь в качестве еще одного номера к множеству натуральных чисел добавлен ноль). В таких случаях, задавая последовательность, указывают, какие значения принимают номера n.

Если в некоторой последовательности для любого n Î N 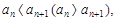то последовательность называется неубывающей (невозрастающей). Такие последовательности называются монотонными.

Пример 1. Числовая последовательность 1, 2, 3, 4, 5, … является рядом натуральных чисел и имеет общий член a_n = n.

Пример 2.Числовая последовательность 2, 4, 6, 8, 10, … является рядом четных чисел и имеет общий член a_n = 2n.

Пример 3.1.4, 1.41, 1.414, 1.4142, … − числовая последовательность приближенных значений с увеличивающейся точностью.

В последнем примере невозможно дать формулу общего члена последовательности.

Пример 4.Записать первых 5 членов числовой последовательности по ее общему члену 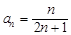. Для вычисления a₁ нужно в формулу для общего члена a_n вместо n подставить 1, для вычисления a₂ − 2 и т. д. Тогда имеем: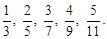

Тест 6. Общим членом последовательности 1, 2, 6, 24, 120, ¼ является:

1)

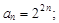
2)

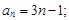
3)

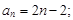
4)

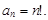
Тест 7. Общим членом последовательности 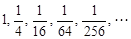является:

1)

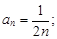
2)

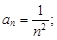
3)

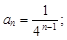
4)

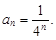
Тест 8. Общим членом последовательности 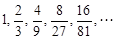является:

1)

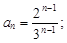
2)

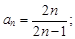
3)

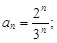
4)