Коническая кривая (эллипс, парабола или гипербола)
Формулы из аналитической геометрии на плоскости
Расстояние 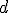 между двумя точками
между двумя точками 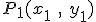 и
и 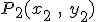
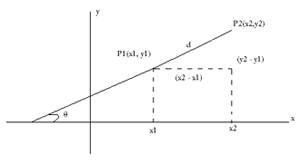
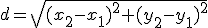
Наклон 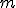 линии, соединяющей две точки
линии, соединяющей две точки 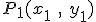 и
и 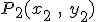
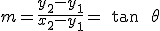
Уравнение линии, соединяющей две точки 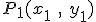 и
и 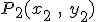
где 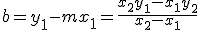 пересечение на
пересечение на 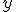 оси, т.e.
оси, т.e. 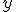 пересечение.
пересечение.
Уравнение линии в условиях 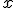 пересекает
пересекает 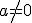 и
и 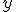 пересекает
пересекает 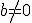
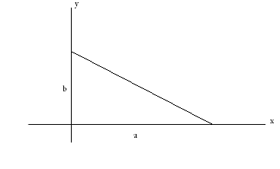
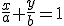
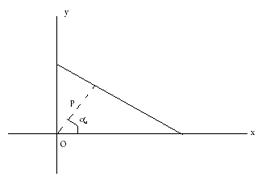
Нормальная форма уравнения линии
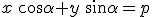
где 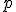 = перпендикулярное расстояние от центра
= перпендикулярное расстояние от центра 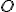 к линии
к линии
и α = Угол наклона перпендикуляра
с положительной 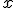 осью.
осью.
Общее уравнение линии
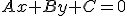
Расстояние от точки 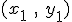 к линии
к линии 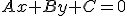
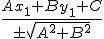
где знак выбирается так, что расстояние не отрицательно.
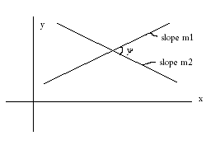
Угол 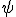 между двумя линиями, имеющими наклоны
между двумя линиями, имеющими наклоны 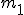 и
и 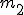
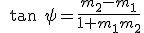
Линии параллельны или совпадают тогда и только тогда, когда 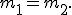
Линии перпендикулярны тогда и только тогда, когда 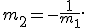
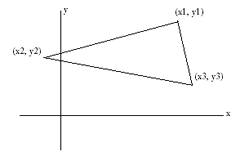
Площадь треугольника с вершинами в 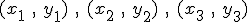
Площадь
где знак выбран так, что площадь является неотрицательной. Если площадь равна нулю, все точки лежат на одной прямой.
Преобразование координат при перемещении
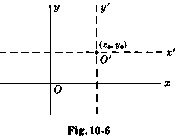
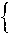 | x = x' + x0 y = y' + y0 | or | 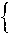 | x' = x - x0 y' = y - y0 |
где (x, y) называются старыми координатами [т.e. координаты относительно xy системы], (x',y') новые координаты [относительно x'y' системы] и (x0, y0) координаты нового центра 0' относительно старой xy координатной системы.
Преобразование координат при вращении
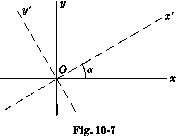
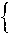 | x = x' cosα - y' sinα y = x' sinα + y' cosα | or | 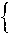 | x' = x cosα + y sinα y' = y cosα - x sinα |
где центры старой [xy] и новой [x'y'] координатной системы те же самые, но x' ось образовывает угол α с положительной x осью.
Преобразование координат при перемещении и вращении
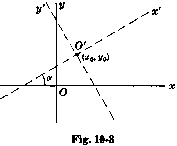
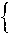 | x = x' cosα - y' sinα + x0 y = x' sinα + y' cosα + y0 | or | 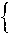 | x' = (x - x0)cosα + (y - y0)sinα y' = (y - y0)cosα - (x - x0)sinα |
где новый центр O' координатной системы x'y' имеет координаты (x0, y0) относительно старой xy координатной системы и ось x' образовывает угол α с положительной осью x .
Полярные координаты (r, θ)
Точка P может быть определена прямоугольными координатами (x, y) или полярными координатами (r, θ). Преобразование между этими двумя координатами:
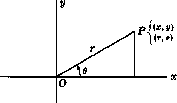
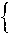
x = r cosθ
y = r sinθ
or
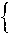
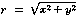
θ = tan-1(y/x)
Уравнение окружности
Уравнение окружности радиуса R, с центром в (x0,y0)
(x - x0)2 + (y - y0)2 = R2
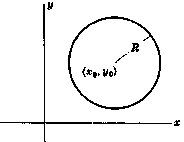
Уравнение окружности радиуса R , проходящей через центр координат
r = 2R cos(θ — α)
где (θ, α) полярные координаты любой точки на окружности и (R, α) полярные координаты центра окружности.
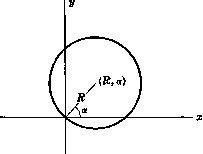
Коническая кривая (эллипс, парабола или гипербола)
Если точка P движется так, что расстояние от фиксированной точки [называемой фокусом] разделенное этим расстоянием от фиксированной линии [называемой директриссой] есть постоянной e [называется эксцентриситет], тогда кривая, описываемая P называется конической[она называется так потому, что такие кривые могут быть получены в результате пересечения плоскости и конуса под различными углами].
Если фокус выбран в начале координатO уравнение конической кривой в полярных координатах (r, θ) есть, если OQ = p и LM = D,
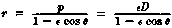
Коническая кривая есть
(i) эллипсом если ε < 1
(ii) параболой если ε = 1
(iii) гиперболой если ε > 1.
Эллипс с центром в 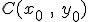 и большей осью, параллельной
и большей осью, параллельной 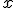 ось
ось
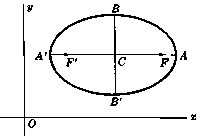
Длина большей оси 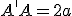
Длина малой оси 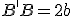
Расстояние от центра 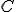 к фокусу
к фокусу 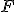 или
или 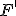 есть
есть
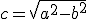
Эксцентриситет = 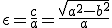
Уравнение в прямоугольных координатах:
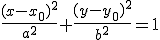
Уравнение в прямоугольных координатах если 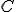 есть в
есть в 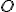 :
:
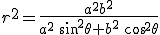
Уравнение в прямоугольных координатах если 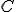 на
на 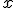 оси и
оси и 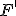 в
в 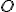 :
:
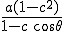
Если 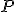 есть любая точка на эллипсе,
есть любая точка на эллипсе, 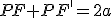
Если большая ось параллельна 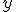 оси, меняем местами
оси, меняем местами 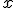 и
и 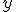 вверху или заменяем
вверху или заменяем 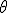 на
на 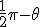 [или
[или 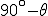 ]
]
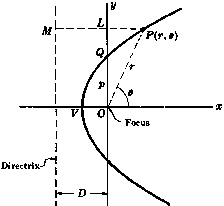
Парабола с осью, параллельной 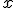 ось
ось
Если вершина в 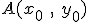 и расстояние между
и расстояние между 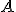 к фокусу
к фокусу 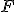 есть
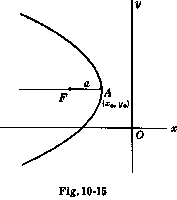
есть 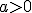 , уравнение параболы есть следующее, если парабола открыта справа
, уравнение параболы есть следующее, если парабола открыта справа
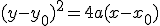
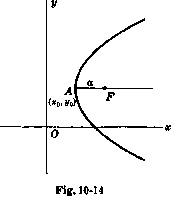
Если парабола открыта слева
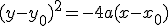
Если фокус находится в центре координат, уравнение в полярных координатах есть
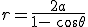
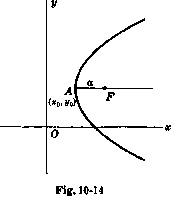

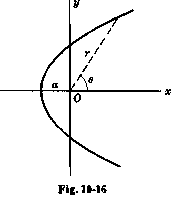
В случае, если ось параллельна 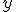 оси, меняя
оси, меняя 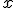 и
и 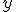 или заменяя
или заменяя 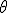 на
на 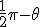 [или
[или 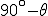 ].
].
Гипербола с центром 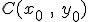 и большей осью, параллельной к
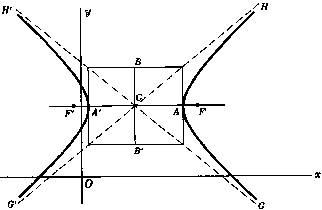
и большей осью, параллельной к 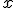 ось
ось
Длина большой оси 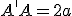
Длина малой оси 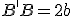
Расстояние от центра 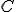 к фокусу
к фокусу 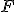 или
или 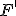 есть
есть
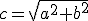
Эксцентриситет = 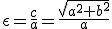
Уравнение в прямоугольных координатах:
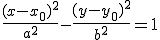
Наклоны асимптоты 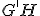 и
и 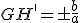
Уравнение в полярных координатах, если 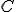 в
в 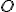 :
:
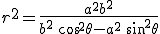
Уравнение в полярных координатах, если 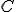 на
на 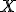 оси и
оси и 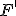 в
в 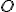 :
:
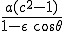
Если 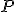 в любой точке на гиперболе,
в любой точке на гиперболе, 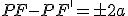 [в зависимости от ветки]
[в зависимости от ветки]
Если большая ось параллельна 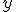 оси, меняя
оси, меняя 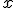 и
и 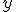 вверху или заменяя
вверху или заменяя 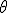 на
на 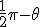 [или
[или 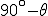 ]
]
