Определение объема и координат центра тяжести жидкого металла в металлургических сосудах

Металлы и сплавы в металлургии производят преимущественно в жидком виде. В качестве металлургических сосудов используют агрегаты (конвертеры, дуговые сталеплавильные печи и др.), миксеры, ковш, изложницы, шлаковые чаши и т.п.

Для слива металла многие сосуды приходится кантовать, а для расчета привода кантования необходимо определять статический момент сопротивления повороту сосуда от силы тяжести жидкого металла в нем. По мере слива металла меняются его объем и координаты центра тяжести, соответственно изменяется и статический момент сопротивления.

Координаты центра тяжести жидкого металла в общем случае определяются по формулам:

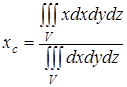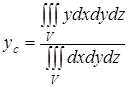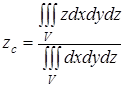; ; , (57)

где V – объем металла, ограниченный плоскостью его поверхности и внутренней поверхностью сосуда.

Известные графоаналитические методы расчета объема и координат центра тяжести жидкого металла отличаются значительной трудоемкостью и невысокой точностью [9]. Рассмотрим универсальный метод решения задачи с использованием ЭВМ [10].

Полость сосуда имеет плоскость симметрии, перпендикулярную поверхности металла, с которой совмещается плоскость координат XOY (рисунок 27). Для решения задачи должно быть задано уравнение боковой поверхности сосуда: z_п=f(x, y). Положение плоскости “зеркала” металла характеризуется углом j.

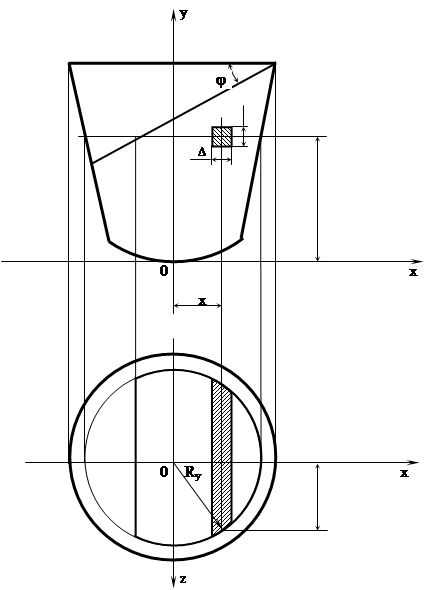Рисунок 27 – Расчетная схема металлургического сосуда

Идея метода заключается в следующем. Объем жидкого металла горизонтальными и вертикальными сечениями разбивается на элементарные призмы, перпендикулярные плоскости координат XOY. На рисунке 27 показана элементарная призма со стороной основания D и длиной 2 z_п, выделенная горизонтальным сечением на расстоянии y и вертикальным сечением на расстоянии х. Площадь основания призмы S=D´D, а объем – V=2D²z_п , где z_п – длина полупризмы, определяемая по выражению:

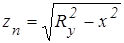, (58)

где R_y – радиус окружности в сечении сосуда на расстоянии y.

Величина z_п будет изменяться для каждой призмы. Тогда, если в формулах (57) перейти от интегралов к суммам, то координаты центра тяжести жидкого металла можно вычислить по выражениям:

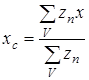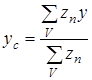; . (59)

Объем металла для заданного угла наклона j его поверхности:

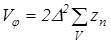, (60)

где 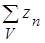- сумма полудлин призм по всему объему жидкого металла, определяемая как

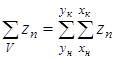, (61)

где y_н, y_к, х_н, х_к – начальные и конечные координаты, характеризующие расположение горизонтальных и вертикальных сечений в объеме жидкого металла.

Масса жидкого металла в сосуде для заданного угла наклона j его поверхности вычисляется как

m = rV_j . (62)

В качестве примера рассмотрим решение задачи для кислородного конвертера, так как объемные тела, которые выделяются в конвертере, могут встретиться и при решении задачи для других металлургических сосудов.

Расчетная схема приведена на рисунке 28. На нем обозначены следующие части, на которые можно разбить объем жидкого металла в конвертере: 1 – верхний конический пояс; 2 – цилиндрический пояс; 3 – нижний конический пояс; 4 – сферический сегмент, усеченные плоскостью поверхности жидкого металла.

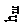
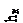
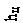
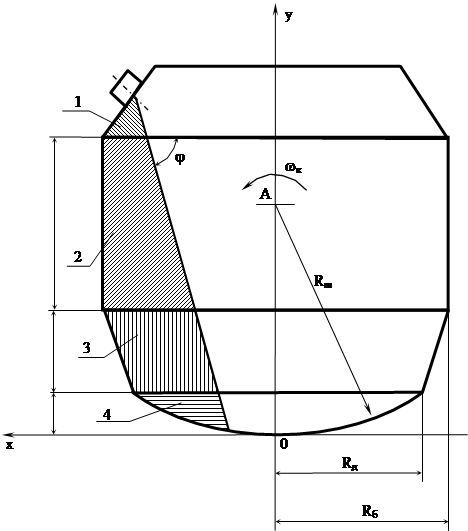
Рисунок 28 – Расчетная схема конвертера

Рассмотрим определение координат центра тяжести для каждой из перечисленных частей. На рисунке 29 представлена расчетная схема цилиндрического пояса.

Для данной фигуры радиус окружности для любого сечения y постоянен и равен:

R_y = R_б .

где R_б – радиус цилиндрической части.

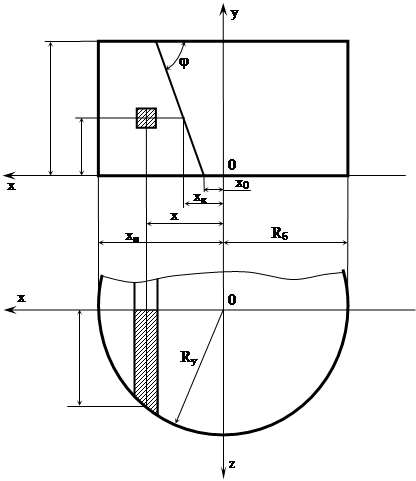
Рисунок 29 – Цилиндрический пояс

Начальные и конечные координаты, характеризующие расположение горизонтальных и вертикальных сечений в объеме жидкого металла, вычисляются по выражениям:

y_н = 0 ; y_к = h_ц ; x_н = R_б ; x_к = x₀ + ,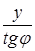

где h_ц – высота цилиндрической части;

х₀ - координата, определяющая положение плоскости металла в сечении y=0;

y - текущая координата, характеризующая расположение горизонтального сечения, изменяющаяся с шагом D, т.е. y = y + D .

Текущая координата, характеризующая расположение вертикального сечения, изменяется с шагом (-D):

x = x - D .

Длина полупризмы z_п вычисляется по формуле (59).

Блок-схема алгоритма нахождения координат центра тяжести, объема и массы жидкого металла в цилиндрической части приведена на рисунке 30.

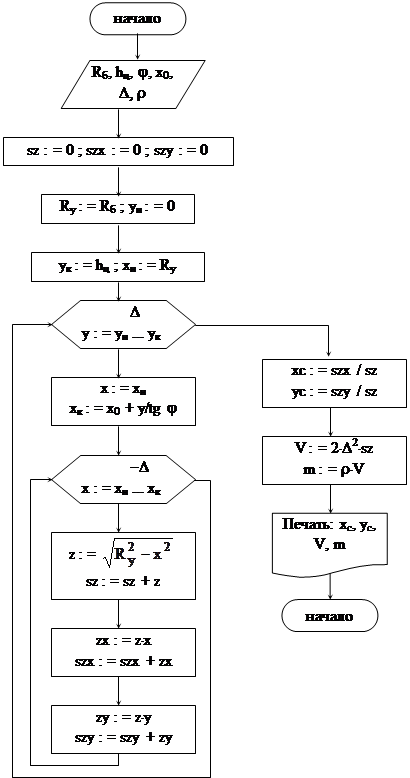Рисунок 30 – Блок-схема алгоритма для цилиндрического пояса

Рассматриваем нижний конический пояс (рисунок 31).

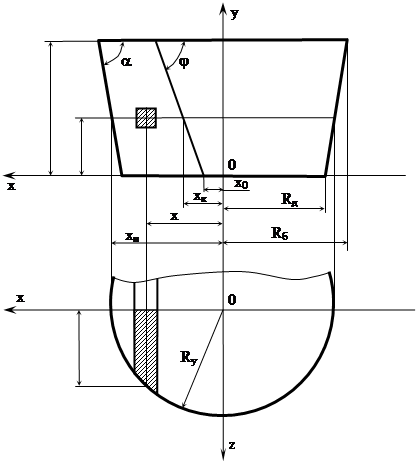
Рисунок 31 – Конический пояс

В коническом поясе величина R_y будет переменной для каждого горизонтального сечения:

R_y = R_д + ,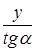

где R_д – радиус донной части конвертера;

a - угол наклона образующей конического пояса:

,

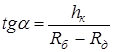где h_к – высота конического пояса.

Тогда, R_y = R_д + .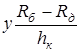

Остальные расчетные формулы имеют вид :

y_н = 0 ; y_к = h_к ; y = y + D ;

x_н = R_y ; x_к = x₀ + 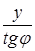; x = x - D .

Блок-схема алгоритма для конического пояса приведена на рисунке 32.

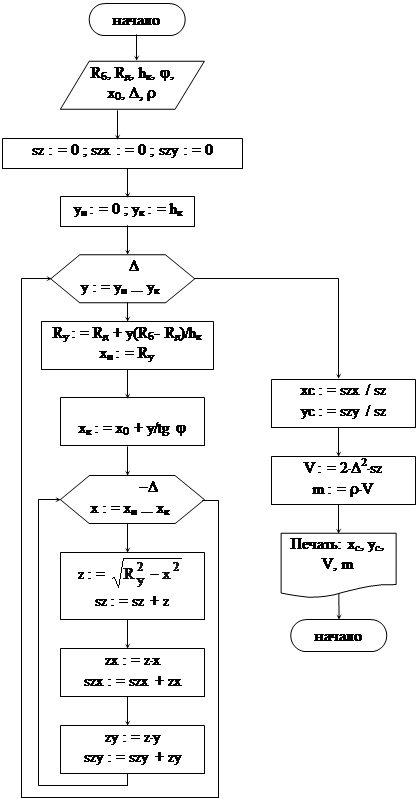
Рисунок 32 – Блок-схема алгоритма для конического пояса

Рассматриваем шаровой сегмент. Расчетная схема приведена на рисунке 33.

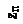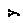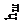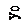Рисунок 33 – Шаровой сегмент

В шаровом коническом сегменте величина R_y также будет переменной для каждого горизонтального сечения:

,

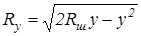где R_ш - радиус шарового сегмента.

Расчетные формулы:

y_н = y₀ ; y_к = h_ш ; y = y + D ;

x_н = R_y ; x_к = x₀ + 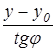; x = x - D ,

где h_ш – высота шарового сегмента;

y₀ - координата, определяющая начальное положение плоскости металла.

Блок-схема алгоритма для шарового сегмента приведена на рисунке 34.

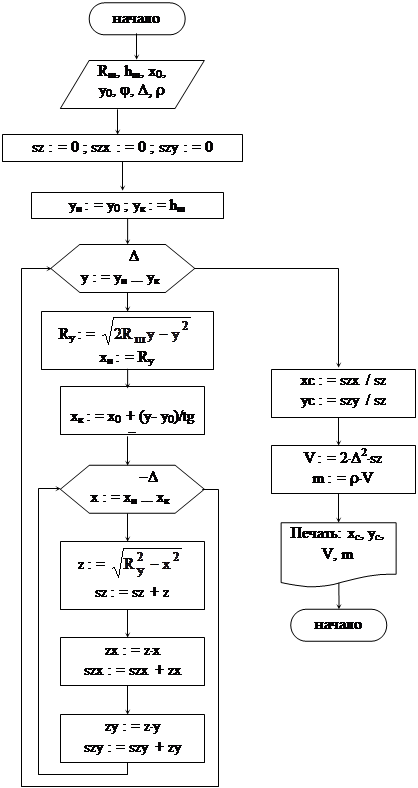Рисунок 34 – Блок-схема алгоритма для шарового сегмента

Координаты центра тяжести всего жидкого металла в конвертере определяются по формуле:

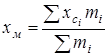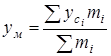; , (63)

где 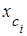, , 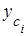m_i – координаты центра тяжести и масса жидкого металла в i-й части конвертора.

Масса металла в конвертере для заданного угла поворота j :

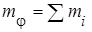. (64)

Численные методы решения