Системы линейных уравнений и неравенств
Системой m линейных уравнений с n неизвестными x1, x2, ¼, xn называется система вида
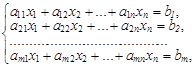 (1)
(1)
где аij и bi – действительные числа (i = 1, 2, …, m; j = 1, 2, …, n), которые называются соответственно коэффициентами при неизвестных и свободными членами уравнений системы (1).
Матрица А = 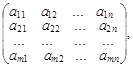 составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1).
составленная из коэффициентов при неизвестных системы (1), называется матрицей системы (1).
Матрица-столбец В = 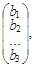 составленная из свободных членов уравнений системы (1), называется столбцом свободных членов системы (1).
составленная из свободных членов уравнений системы (1), называется столбцом свободных членов системы (1).
Матрица системы (1), дополненная столбцом свободных членов системы (1), называется расширенной матрицей системы (1):
АВ = 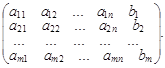
Пример 1. Для системы линейных уравнений
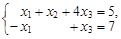 матрица системы – А =
матрица системы – А = 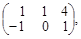 расширенная матрица системы – АВ =
расширенная матрица системы – АВ = 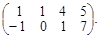
Тест 1. Для системы линейных уравнений 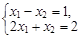 матрица системы имеет вид:
матрица системы имеет вид:
1) А = 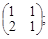
2) А = 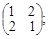
3) А = 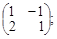
4) А = 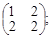
5) А = 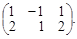
Тест 2. Для системы линейных уравнений 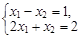 расширенная матрица системы имеет вид:
расширенная матрица системы имеет вид:
1) АB = 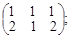
2) АB = 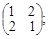
3) АB = 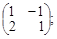
4) АB = 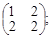
5) АB = 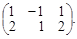
Решением системы уравнений (1) называется упорядоченная совокупность n чисел (l1; l2; ¼; ln), при подстановке которых вместо
х1, х2, …, хn соответственно (х1 = 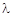 1; х2 =
1; х2 = 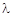 2; …; хn =
2; …; хn = 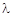 n) каждое уравнение системы (1) обращается в верное равенство.
n) каждое уравнение системы (1) обращается в верное равенство.
Пример 2. Определить, является ли упорядоченная совокупность чисел (1; 3) решением системы линейных уравнений 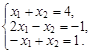
Решение
Подставим в каждое уравнение данной системы вместо х1 первое число из данной упорядоченной совокупности, а вместо х2 – второе. Первое и второе уравнения обратятся в верные равенства
1 + 3 = 4,
2 × 1 – 3 = –1.
А третье уравнение – нет: –1 + 3 ¹ 1.
Следовательно, упорядоченная совокупность чисел (1; 3) не является решением данной системы линейных уравнений.
Ответ: нет.
Тест 3. Определить, является ли упорядоченная совокупность чисел (1; 2; 3) решением системы линейных уравнений 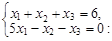
1) да;
2) нет.
Тест 4. Определить, является ли упорядоченная совокупность чисел (0; –1) решением системы линейных уравнений 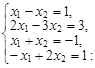
1) да;
2) нет.
Система уравнений (1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной.
Теорема (правило Крамера). Пусть Δ – определитель матрицы системы n линейных уравнений с n неизвестными х1, х2, …, хn. Если Δ ¹ 0, то система имеет единственное решение, определяемое по формулам
х1 = 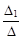 ; х2 =
; х2 = 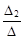 ; …; хn =
; …; хn = 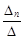 ,
,
где 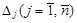 – определитель, полученный из определителя Δ заменой в нем j-го столбца столбцом свободных членов системы.
– определитель, полученный из определителя Δ заменой в нем j-го столбца столбцом свободных членов системы.
Пример 3. Решить систему линейных уравнений по правилу Крамера:
1) 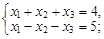
2) 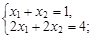
3) 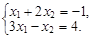
Решение
1. Уравнений в системе – 2, а неизвестных – 3. Так как правило Крамера применимо только для систем, у которых число уравнений и число неизвестных совпадают, то данную систему решить по правилу Крамера нельзя.
Ответ: правило Крамера неприменимо.
2. Уравнений в системе – 2, неизвестных – 2. Матрица данной системы имеет вид А = 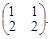 Составим Δ – определитель матрицы системы: Δ =
Составим Δ – определитель матрицы системы: Δ = 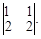
Найдем его значение, используя правило вычисления определителей матрицы второго порядка: Δ = 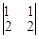 =
= 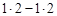 = 2 – 2 = 0.
= 2 – 2 = 0.
Так как Δ = 0, то решить данную систему по правилу Крамера нельзя.
Ответ: правило Крамера неприменимо.
3. Уравнений в системе – 2, неизвестных – 2. Матрица данной системы имеет вид А = 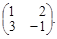 Составим Δ – определитель матрицы системы: Δ =
Составим Δ – определитель матрицы системы: Δ = 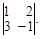
Найдем его значение, используя правило вычисления определителей матрицы второго порядка: Δ = 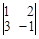 = 1 × (–1) – 2 × 3 = –1 – 6 = –7 ¹ 0.
= 1 × (–1) – 2 × 3 = –1 – 6 = –7 ¹ 0.
Итак, нам дана система двух линейных уравнений с двумя неизвестными и Δ ¹ 0. Значит, к данной системе правило Крамера применимо.
Применим его. Так как по правилу Крамера х1 = 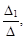 х2 =
х2 = 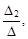 найдем значения Δ1 и Δ2. Определитель Δ1 получается из определителя Δ заменой в нем 1-го столбца столбцом свободных членов системы. Столбец
найдем значения Δ1 и Δ2. Определитель Δ1 получается из определителя Δ заменой в нем 1-го столбца столбцом свободных членов системы. Столбец 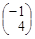 – столбец свободных членов системы. Следовательно, Δ1 =
– столбец свободных членов системы. Следовательно, Δ1 = 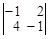 =
= 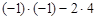 = 1 – 8 = –7.
= 1 – 8 = –7.
Определитель Δ2 получается из определителя Δ заменой в нем 2-го столбца столбцом свободных членов системы. Следовательно,
Δ2 = 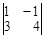 =
= 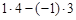 = 4 + 3 = 7.
= 4 + 3 = 7.
Тогда: х1 = 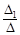 =
= 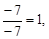 х2 =
х2 = 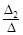 =
= 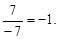
Ответ: (1; –1).
Тест 5. При решении системы линейных уравнений 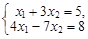 по правилу Крамера определитель Δ имеет вид:
по правилу Крамера определитель Δ имеет вид:
1) 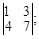
2) 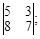
3) 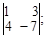
4) 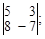
5) 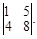
Тест 6. При решении системы линейных уравнений 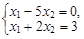 по правилу Крамера определитель Δ1 имеет вид:
по правилу Крамера определитель Δ1 имеет вид:
1) 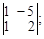
2) 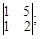
3) 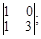
4) 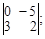
5) 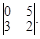
Тест 7. При решении системы линейных уравнений 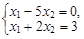 по правилу Крамера определитель Δ2 имеет вид:
по правилу Крамера определитель Δ2 имеет вид:
1) 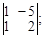
2) 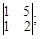
3) 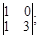
4) 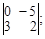
5) 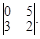
Тест 8. При решении системы двух линейных уравнений с двумя неизвестными х1 и х2 по правилу Крамера получены значения: Δ = 4, Δ1 = 8, Δ2 = 2. Система имеет решение:
1) (8; 2);
2) ( 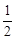 ; 2);
; 2);
3) (4; 8; 2);
4) (8; 2; 4);
5) (2; 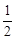 ).
).
Тест 9.Решить систему линейных уравнений 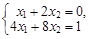 по правилу Крамера:
по правилу Крамера:
1) (2; –1);
2) правило Крамера неприменимо;
3) (1; 2);
4) (2; 1);
5) (1; 1).
Тест 10. Решить систему линейных уравнений 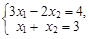 по правилу Крамера:
по правилу Крамера:
1) (2; –1);
2) правило Крамера неприменимо;
3) (1; 2);
4) (2; 1);
5) (1; 1).
Тест 11. Решить систему линейных уравнений 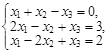 по правилу Крамера:
по правилу Крамера:
1) (1; 1; 1);
2) (0; 1; 1);
3) (0; 0; 1);
4) (1; 0; 1);
5) правило Крамера неприменимо.
Две системы уравнений называются эквивалентными, или равносильными, если они имеют одно и то же множество решений. Любые две несовместные системы считаются эквивалентными.
Тест 12. Ступенчатая система, эквивалентная исходной системе линейных уравнений, имеет вид 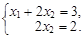
Решением исходной системы является:
1) (0; 1);
2) (1; 2);
3) (2; 1);
4) (1; 1);
5) (–1; 0).
Тест 13. Ступенчатая система, эквивалентная исходной системе линейных уравнений, имеет вид 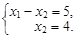
Решением исходной системы является:
1) (4; 9);
2) (4; 1);
3) (1; 4);
4) (9; 4);
5) (9; 1).
Линейным неравенством с двумя неизвестными х, у называется неравенство вида: ax + by + c £ 0 или ax + by + c £ 0, где a, b, c – действительные числа.
Решением линейного неравенства с двумя неизвестными х, у называется всякая упорядоченная пара действительных чисел (l1; l2), в результате подстановки которых вместо х, у соответственно неравен-
ство превращается в верное числовое неравенство.
С геометрической точки зрения пару действительных чисел (l1; l2), являющуюся решением линейного неравенства с двумя неизвестными х, у, можно рассматривать как координаты точки плоскости Оху.
Областью решений линейного неравенства с двумя неизвестными х, у называется множество точек плоскости Оху, координаты которых удовлетворяют этому неравенству.
Теорема. Областью решений линейного неравенства с двумя неизвестными х, у вида ax + by + c ³ 0 служит одна из двух полуплоскостей, на которые всю плоскость Оху делит прямая ax + by + c = 0, включая и эту прямую, а другая полуплоскость вместе с той же прямой является областью решений неравенства ax + by + c £ 0.
Пример 4. Построить область решений неравенства х + у + 2 ³ 0.
Решение
х + у + 2 ³ 0 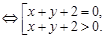
1. На плоскости Оху построим прямую х + у + 2 = 0 по двум точкам (рисунок 19): если х = 0, то у = –2, имеем точку (0; –2); если х = 2, то
у = –4, имеем точку (2; –4).
2. Возьмем произвольную точку, не лежащую на прямой х + у + 2 = 0.
Применяя теорему, имеем:
1) если координаты взятой точки удовлетворяют неравенству х + у +
+ 2 > 0, то искомой будет полуплоскость, содержащая взятую точку;
2) если координаты взятой точки не удовлетворяют неравенству
х + у + 2 > 0, то искомой будет полуплоскость, не содержащая взятую точку.
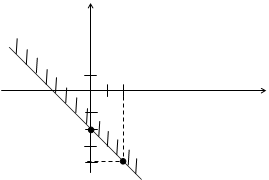 |
у
02 х
–2
–4 х + у + 2 = 0
Рисунок 19
Возьмем, например, точку (0; 0). Подставим ее координаты в неравенство х + у + 2 > 0. Получим 0 + 0 +2 > 0 или 2 > 0 – верное неравенство. Следовательно, искомой будет полуплоскость, содержащая точку (0; 0).
Теорема. Область решений системы линейных неравенств с двумя неизвестными есть пересечение (общая часть) полуплоскостей, каждая из которых есть область решения соответствующего неравенства системы.
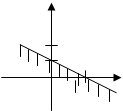
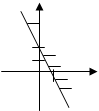
Тест 14.Решением неравенства 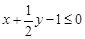 является полуплоскость:
является полуплоскость:
1) 2)
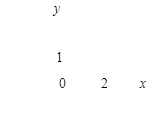
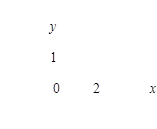
3) 4) 5)
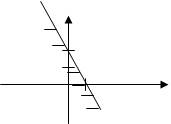
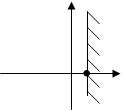
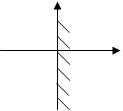
Тест 15.Решением неравенства х ³ 0 является полуплоскость:
1) 2) 3)
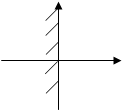
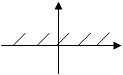
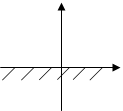
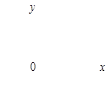
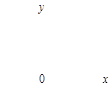
4) 5)
Тест 16. Решением системы линейных неравенств 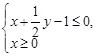 является часть плоскости:
является часть плоскости:
1) 2) 3)
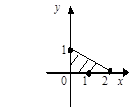
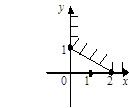
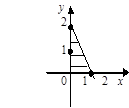
4) 5)
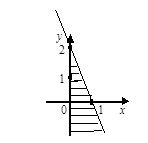
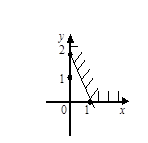
Ответы на тестовые задания
| Номер теста | |||||||||
| Правильный ответ |
| Номер теста | |||||||
| Правильный ответ |
Комплексные числа
Комплексным числом z называется выражение вида z = а + bi, где а и b – действительные числа, i – мнимая единица, i2 = –1.
Если а = 0, то число 0 + bi = bi называется чисто мнимым; если
b = 0, то число а + 0i = а отождествляется с действительным числом а.
Таким образом, множество R всех действительных чисел является подмножеством множества С всех комплексных чисел, т. е. R Ì С.
Для комплексного числа z = a +bi число а называется действительной частью комплексного числа z и обозначается а = Rez, а число b – мнимой частью комплексного числа z и обозначается b = Imz.
Пример 1. Для комплексного числа z определить Rez и Imz:
а) z = 2 + 5i;
б) z = 1 – 3i;
в) z = 2;
г) z = 5i;
д) z = i.
Решение
а) Rez = 2, Imz = 5;
б) так как z = 1 – 3i = 1 + (–3)i, то Rez = 1, Imz = –3;
в) так как z = 2 = 2 + 0i, то Rez = 2, Imz = 0;
г) так как z = 5i = 0 + 5i, то Rez = 0, Imz = 5;
д) так как z = i = 0 + 1i, то Rez = 0, Imz = 1.
Тест 1. Мнимая часть Imz комплексного числа z = 5 + 4i равна:
1) 9;
2) 5;
3) 4;
4) (–4);
5) 1.
Тест 2. Мнимая часть Imz комплексного числа z = 7 – i равна:
1) 7;
2) 1;
3) 0;
4) (–1);
5) (–7).
Тест 3. Действительная часть Rez комплексного числа z = –4i равна:
1) –4;
2) 0;
3) 4;
4) 1;
5) (–1).
Два комплексных числа z1 = а1 + b1i и z2 = а2 + b2i называются равными тогда и только тогда, когда равны их действительные части и равны их мнимые части, т. е. а1 = а2, b1 = b2. В частности, комплексное число z = а + bi равно нулю тогда и только тогда, когда а = b = 0.
Пример 2. Указать, какие из комплексных чисел являются равными: z1 = 2 + 3i; z2 = 2 + 5i; z3 = 1 + 3i; z4 = –1 + 3i; z5 = 2 + 3i.
Решение
Среди данных комплексных чисел выбираем сначала те, которые имеют равные действительные части: z1, z2, z5. Так как при этом Imz1 =
= Imz5 = 2, Imz2 = 5, то равными являются комплексные числа z1 и z5.
Ответ: z1 = z5.
Тест 4. Даны комплексные числа: z1 = 2 + 3i; z2 = 4 – i; z3 = 3 + 2i; z4 = –4 + i; z5 = 4 + i; z6 = 4 – i; z7 = 2 – 3i; z8 = 4 – i; z9 = 3 – 2i. Среди них равными являются:
1) z1 = z3 = z7 = z9;
2) z7 = z9;
3) z2 = z5 = z6 = z8;
4) z2 = z4;
5) z2 = z6 = z8.
Два комплексных числа z = а + bi и 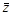 = а – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
= а – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.
Пример 3. Указать число, сопряженное к комплексному числу z = 7 – i.
Решение
Сопряженным к данному комплексному числу будет комплексное число 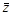 = 7 + i.
= 7 + i.
Ответ: 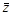 = 7 + i.
= 7 + i.
Тест 5. Указать число, сопряженное к комплексному числу z = 2 + 3i:
1) 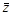 = 2 – 3i;
= 2 – 3i;
2) 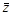 = –2 – 3i;
= –2 – 3i;
3) 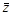 = –2 – 3i;
= –2 – 3i;
4) 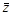 = 2 + 3i;
= 2 + 3i;
5) 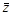 = 3 + 2i.
= 3 + 2i.
Тест 6. Указать число, сопряженное к комплексному числу z = 3i:
1) 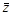 = 3i;
= 3i;
2) 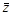 = 0;
= 0;
3) 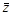 = –3i;
= –3i;
4) 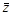 = 1;
= 1;
5)  = –1.
= –1.
Запись числа z в виде z = а + bi называется алгебраической формой комплексного числа.
Рассмотрим действия над комплексными числами, заданными в алгебраической форме. Если z1 = а + bi, z2 = с + di, то
z1 + z2 = (а + bi) + (с + di) = а + bi + с + di = (а + с) + (b + d)i; (1)
z1 – z2 = (а + bi) – (с + di) = а + bi – с – di = (а – с) + (b – d)i. (2)
Пример 4. Даны два комплексных числа z1 = 2 + i и z2 = 4 – 3i. Найти их сумму и разность.
Решение
В соответствии с формулами (1), (2) при а = 2, b = 1, с = 4, d = –3 получаем
z1 + z2 = (2 + i) + (4 – 3i) = 2 + i + 4 – 3i = (2 + 4) + (1 – 3)i = 6 – 2i;
z1 – z2 = (2 + i) – (4 – 3i) = 2 + i – 4 + 3i = (2 – 4) + (1 + 3)i = –2 + 4i.
Ответ: 6 – 2i; –2 + 4i.
Тест 7. Сумма комплексных чисел z1 = 1 + i и z2 = 2 – 2i равна:
1) 4 – i;
2) 3 – i;
3) 5 + i;
4) 5;
5) 3 + i.
Тест 8.Разность комплексных чисел z1 = 3 + i и z2 = 4 – 2i равна:
1) –1 – i;
2) 1+ i;
3) 1 – 3i;
4) –1 + 3i;
5) 1 – i.
Рассмотрим плоскость с декартовой прямоугольной системой координат Оxy. Всякое комплексное число z = a + bi можно изобразить точкой М(a; b) на плоскости Оxy такой, что а = Rez, b = Imz. И, наоборот, каждую точку М(a; b) координатной плоскости Оxy можно рассматривать как образ комплексного числа z = a + bi (рисунок 20).
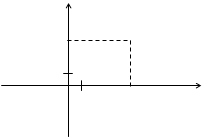
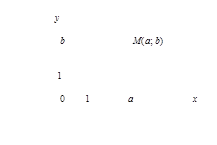
Рисунок 20
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней изображены действительные числа z = a +0i = а. Ось ординат называется мнимой осью, так как на ней изображены чисто мнимые комплексные числа z = 0 + bi = bi.
Пример 5.На комплексной плоскости изобразить число z = 2 – 3i.
Решение
Для данного комплексного числа а = Rez = 2, b = Imz = –3. На координатной плоскости Оxy (рисунок 21) число z = 2 – 3i изображается точкой М(2; –3).
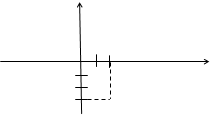 |
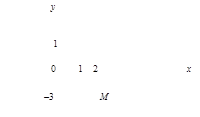
Рисунок 21
Комплексное число z = а + bi, заданное в алгебраической форме, можно представить и в другом виде. Изобразим число z точкой М(а; b) комплексной плоскости. Рассмотрим радиус-вектор 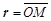 этой точки (рисунок 22).
этой точки (рисунок 22).
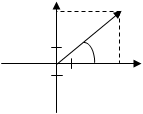
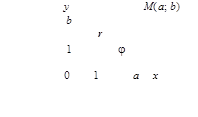
Рисунок 22
Тест 9. Указать, на какой комплексной плоскости точка М является изображением комплексного числа z = –5 + 2i:
1) 2) 3)
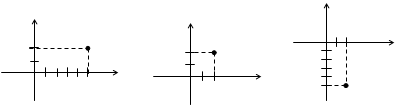
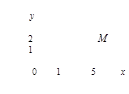
4) 5)
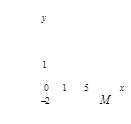
Тест 10. Указать, на какой комплексной плоскости точка М является изображением комплексного числа z = –2i:
1) 2) 3)
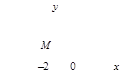
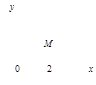
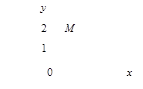
4) 5)
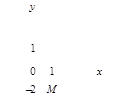
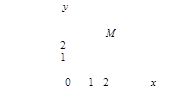
Модулем комплексного числа z = а + bi называется длина радиуса-вектора 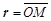 точки М(а; b), изображающей данное число.
точки М(а; b), изображающей данное число.
Обозначение: 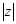 или r.
или r.
Из прямоугольного треугольника ОМа (рисунок 22) по теореме Пифагора 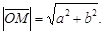 Следовательно,
Следовательно, 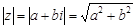 или
или
r 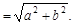
Пример 6. Найти модуль комплексного числа z = 1 – 3i.
Решение
Для данного комплексного числа а = 1, b = –3. Следовательно,
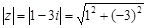 =
= 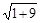 =
= 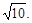
Ответ: 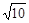 .
.
Тест 11. Модуль комплексного числа z = 4 + 3i равен:
1) 25;
2) 5;
3) 7;
4) 49;
5) 24.
Тест 12. Модуль комплексного числа z = –i равен:
1) –1;
2) 0;
3) 1;
4) 2;
5) 5.
Тест 13. Модуль комплексного числа z = 4 равен:
1) –1;
2) 0;
3) 1;
4) 4;
5) 2.
Аргументом комплексного числа z = а + bi называется величина угла φ (рисунок 22) между положительным направлением действительной оси Ох и вектором r, изображающим комплексное число. Обозначение: аrgz или φ.
Аргумент (главное значение аргумента) комплексного числа заключен в промежутке [0; 2π).
Множество аргументов числа z обозначается Аrgz и Аrgz = аrgz +
+ 2πk, k Î Z.
С помощью модуля r и аргумента φ комплексное число z = а + bi можно представить в другом виде. Так как а = r cosφ, b = r sin φ (рисунок 22), то z = а + bi = r cosφ + r sinφi или z = r (cosφ + i sinφ), где
r = 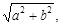 (3)
(3)
cosφ = 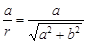 , sin φ =
, sin φ = 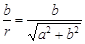 . (4)
. (4)
Запись числа z = а + bi в виде z = r (cosφ + i sinφ), где r – модуль, а φ – аргумент числа z, называется тригонометрической формой комплексного числа z.
Пример 7. Представить комплексное число z = –1 + i в тригонометрической форме.
Решение
z = –1 + i – алгебраическая форма комплексного числа z, при этом а =
= –1, b = 1. Применяя формулы (3), (4), находим r = 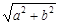 =
=
= 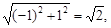 cosφ =
cosφ = 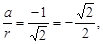 sinφ =
sinφ = 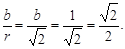
Так как cosφ = 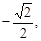 sinφ =
sinφ = 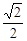 и φ Î [0; 2π), то φ =
и φ Î [0; 2π), то φ = 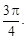 Следовательно, тригонометрическая форма данного числа z имеет вид
Следовательно, тригонометрическая форма данного числа z имеет вид
z = 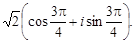
Ответ: z = 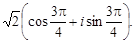
Тест 14. Тригонометрическая форма комплексного числа z =
= 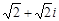 имеет вид:
имеет вид:
1) 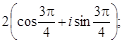
2) 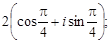
3) 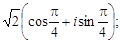
4) 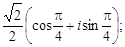
5) 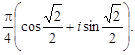
Тест 15. Тригонометрическая форма комплексного числа z = –1 имеет вид:
1) 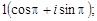
2) 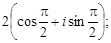
3) 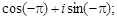
4) 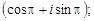
5) 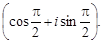
Два комплексных числа z1 = r1(cos φ1 + i sin φ1) и z2 = r2(cosφ2 + i sin φ2), заданных в тригонометрической форме, равны тогда и только тогда, когда их модули равны, а аргументы отличаются на величину, кратную 2π, т. е. z1 = z2 Û r1 = r2, φ1 = φ2 + 2 πk, k Î Z.
Пример 8. Указать, какие из комплексных чисел являются равными: z1 = 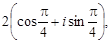 z2 =
z2 = 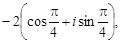
z3 = 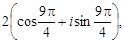 z4 =
z4 = 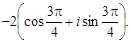
Решение
Среди данных комплексных чисел выбираем сначала те, которые имеют равные модули: z1, z3, z4.Так как φ1 = 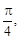 φ3 =
φ3 = 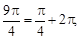
φ4 = 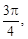 то равными являются комплексные числа z1 и z3.
то равными являются комплексные числа z1 и z3.
Ответ: z1 = z3.
Тест 16. Даны комплексные числа z1 = 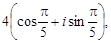 z2 =
z2 =
= 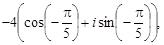 z3 =
z3 = 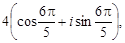 z4 =
z4 =
= 4 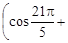 +
+ 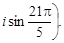 Среди них равными являются:
Среди них равными являются:
1) z1 = z2;
2) z1 = z3;
3) z1 = z4;
4) z2 = z3;
5) z3 = z4.
Формула Эйлера имеет следующий вид:
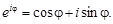 (5)
(5)
Данная формула может быть записана в виде
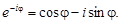 (6)
(6)
Из формул (5) и (6) следует
сos 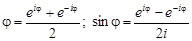 .
.
Используя формулу (5), комплексное число z = r(cosφ + i sinφ) можно записать в виде z = rеiφ, называемом показательной (или экспоненциальной) формой комплексного числа z.
Пример 9. Представить комплексное число z = 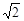
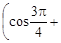 i sin
i sin 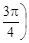 в показательной форме.
в показательной форме.
Решение
z = 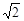
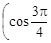 + i sin
+ i sin 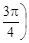 – тригонометрическая форма комплексного числа z, при этом r =
– тригонометрическая форма комплексного числа z, при этом r = 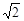 , φ =
, φ = 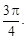
Поэтому показательная форма данного числа z имеет вид z = 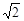 e
e 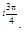
Ответ: z = 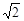 e
e 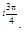
Тест 17. Показательная форма комплексного числа z = 2 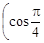 +
+
+ i sin 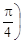 имеет вид:
имеет вид:
1) 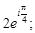
2) 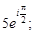
3) 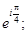
4) 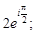
5) 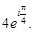
Тест 18.Показательная форма комплексного числа z = –1 + i имеет вид:
1) 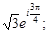
2) 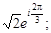
3) 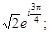
4) 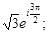
5) 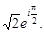
Ответы на тестовые задания
| Номер теста | ||||||||||
| Правильный ответ | ||||||||||
| Номер теста | ||||||||||
| Правильный ответ |
Раздел II. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
