| | | Найти центр пучка прямых, данного уравнением  . .  |
| | | Найти уравнение прямой, принадлежащей пучку прямых  и и |
| | 354.1 | Проходящей через точку А(3; -1); |
| | 354.2 | Проходящей через начало координат; |
| | 354.3 | Параллельной оси Ox; |
| | 354.4 | Параллельной оси Oy; |
| | 354.5 | Параллельной прямой  ; ; |
| | 354.6 | Перпендикулярной к прямой  . .  |
| | | Составить уравнение прямой, проходящей через точку пересечения прямых  , ,  и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых. и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых.  |
| | | Составить уравнение прямой, которая проходит через точку пересечения прямых 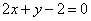 , ,  и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых. и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых.  |
| | | Дано уравнение пучка прямых  . Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1). . Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1).  |
| | | Дано уравнение пучка прямых  . Найти прямую этого пука, проходящую через середину отрезка прямой . Найти прямую этого пука, проходящую через середину отрезка прямой  , заключенного между прямыми , заключенного между прямыми  , ,  . .  |
| | | Даны уравнения сторон треугольника 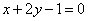 , ,  , ,  . Не определяя координат его вершин, составить уравнения высот этого трегоульника. . Не определяя координат его вершин, составить уравнения высот этого трегоульника.  (ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ). (ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ). |
| | | Составить уравнение прямой, проходящей через точку пересечения прямых  , ,  под углом 450 к прямой под углом 450 к прямой  . Решить задачу, не вычисляя координат точки пересечения данных прямых. . Решить задачу, не вычисляя координат точки пересечения данных прямых.  |
| | | В треугольнике АВС даны уравнения высоты AN:  , высоты BN: , высоты BN:  и стороны АВ: и стороны АВ: 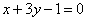 . Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты. . Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты.  |
| | | Составить уравнения сторон треугольника АВС, зная одну его вершину А(2; -1), а также уравнения высоты  и биссектрисы и биссектрисы  , проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С. , проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С.  |
| | | Дано уравнение пучка прямых  . Найти прямые этого пучка, отрезки которых, заключенные между прямыми . Найти прямые этого пучка, отрезки которых, заключенные между прямыми  , ,  , равны , равны  . .  |
| | | Дано уравнение пучка прямых  . Доказать, что прямая . Доказать, что прямая  принадлежит этому пучку. принадлежит этому пучку.  |
| | | Дано уравнение пучка прямых  . Доказать, что прямая . Доказать, что прямая  не принадлежит этому пучку. не принадлежит этому пучку.  |
| | | Дано уравнение пучка прямых  . Найти, при каком значении С прямая . Найти, при каком значении С прямая  будет принадлежать этому пучку. будет принадлежать этому пучку.  |
| | | Дано уравнение пучка прямых  . Найти, при каких значениях a прямая . Найти, при каких значениях a прямая  не будет принадлежать этому пучку. не будет принадлежать этому пучку.  |
| | | Центр пучка прямых  является вершиной квадрата, диагональ которого лежит на прямой является вершиной квадрата, диагональ которого лежит на прямой  . Составить уравнения сторон и второй диагонали этого квадрата. . Составить уравнения сторон и второй диагонали этого квадрата.  |
| | | Дано уравнение пучка прямых  . Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат). . Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат).  |
| | | Дано уравнение пучка прямых  . Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат). . Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат).  |
| | | Дано уравнение пучка прямых  . Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9. . Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9.  |
| | | Дано уравнение пучка прямых  . Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние . Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние  . Написать уравнение этой прямой. . Написать уравнение этой прямой.  |
| | | Дано уравнение пучка прямых  . Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3. . Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3.  |
| | | Составить уравнение прямой, проходящей через точку пересечения прямых 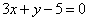 , ,  и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых. и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых.  |
| | | Дано уравнение пучка прямых  . Написать уравнения прямых этого пучка, которые вместе с прямыми . Написать уравнения прямых этого пучка, которые вместе с прямыми 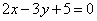 , ,  образуют равнобедренные треугольники. образуют равнобедренные треугольники.  |
| | | Составить уравнение прямой, которая проходит через точку пересечения прямых  , ,  на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых. на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых.  |
| | | Даны уравнения двух пучков прямых  , ,  . Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам. . Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам.  |
| | | Стороны АВ, ВС, CD, DA четырехугольника ABCD заданы соответственно уравнениями  , ,  , ,  , ,  . Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD. . Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD.  |
| | | Центр пучка прямых  является одной из вершин треугольника, две высоты которого даны уравнениями является одной из вершин треугольника, две высоты которого даны уравнениями  , ,  . Составить уравнения сторон этого треугольника. . Составить уравнения сторон этого треугольника.  |
 .
. 
 и
и  ;
;  .
. 
 ,
,  и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых.
и отсекающий на оси ординат отрезок b=-3. Решить задачу, не определяя координат точки пересечения данных прямых. 
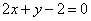 ,
,  и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых.
и делит пополам отрезок, ограниченный точками M1(5; -6), M2(-1; -4). Решить задачу, не вычисляя координат точки пересечения данных прямых. 
 . Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1).
. Написать уравнение прямой этого пучка, проходящей через центр масс однородной треугольной пластинки, вершины которой суть точки A(-1; 2), B(4; -4), C(6; -1). 
 . Найти прямую этого пука, проходящую через середину отрезка прямой
. Найти прямую этого пука, проходящую через середину отрезка прямой  , заключенного между прямыми
, заключенного между прямыми  ,
,  .
. 
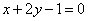 ,
,  ,
,  . Не определяя координат его вершин, составить уравнения высот этого трегоульника.
. Не определяя координат его вершин, составить уравнения высот этого трегоульника.  (ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ).
(ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ).  ,
,  под углом 450 к прямой
под углом 450 к прямой  . Решить задачу, не вычисляя координат точки пересечения данных прямых.
. Решить задачу, не вычисляя координат точки пересечения данных прямых. 
 , высоты BN:
, высоты BN:  и стороны АВ:
и стороны АВ: 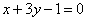 . Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты.
. Не определяя координат вершин и точки пересечения высот треугольника, составить уравнение двух других сторон и третьей высоты. 
 и биссектрисы
и биссектрисы  , проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С.
, проведенных из одной вершины. Решить задачу, не вычисляя координат вершин В и С. 
 . Найти прямые этого пучка, отрезки которых, заключенные между прямыми
. Найти прямые этого пучка, отрезки которых, заключенные между прямыми  ,
,  , равны
, равны  .
. 
 . Доказать, что прямая
. Доказать, что прямая  принадлежит этому пучку.
принадлежит этому пучку. 
 . Доказать, что прямая
. Доказать, что прямая  не принадлежит этому пучку.
не принадлежит этому пучку. 
 . Найти, при каком значении С прямая
. Найти, при каком значении С прямая  будет принадлежать этому пучку.
будет принадлежать этому пучку. 
 . Найти, при каких значениях a прямая
. Найти, при каких значениях a прямая  не будет принадлежать этому пучку.
не будет принадлежать этому пучку. 
 является вершиной квадрата, диагональ которого лежит на прямой
является вершиной квадрата, диагональ которого лежит на прямой  . Составить уравнения сторон и второй диагонали этого квадрата.
. Составить уравнения сторон и второй диагонали этого квадрата. 
 . Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат).
. Найти прямую этого пучка, отсекающую на координатных осях отличные от нуля отрезки равной величины (считая от начала координат). 
 . Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат).
. Найти прямые этого пучка, отсекающие на координатных осях отрезки равной длины (считая от начала координат). 
 . Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9.
. Найти прямые этого пучка, отсекающие от координатных углов треугольники с площадью, равной 9. 
 . Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние
. Доказать, что среди прямых этого пучка существует только одна прямая, отстоящая от точки Р(2; -3) на расстояние  . Написать уравнение этой прямой.
. Написать уравнение этой прямой. 
 . Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3.
. Доказать, что среди прямых этого пучка нет прямой, отстоящей от точки Р(3; -1) на расстояние d=3. 
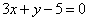 ,
,  и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых.
и отстоящей от точки С(-1; 2) на расстояние d=5. Решить задачу, не вычисляя точки пересечения даных прямых. 
 . Написать уравнения прямых этого пучка, которые вместе с прямыми
. Написать уравнения прямых этого пучка, которые вместе с прямыми 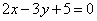 ,
,  образуют равнобедренные треугольники.
образуют равнобедренные треугольники. 
 ,
,  на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых.
на одинаковых расстояниях от точек А(3; -2) и В(-1; 6). Решить задачу, не вычисляя координат точки пересечения данных прямых. 
 ,
,  . Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам.
. Не определяя их центров, составить уравнение прямой, принадлежащей обоим пучкам. 
 ,
,  ,
,  ,
,  . Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD.
. Не определяя координат вершин этого четырехугольника, составить уравнения его диагоналей AC и BD. 
 является одной из вершин треугольника, две высоты которого даны уравнениями
является одной из вершин треугольника, две высоты которого даны уравнениями  ,
,  . Составить уравнения сторон этого треугольника.
. Составить уравнения сторон этого треугольника. 
