Определение и геометрический смысл производной
Пусть функция y = f(x)определена и непрерывна в некоторой окрестности точки x. Тогда приращению Dx независимой переменной 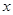 соответствует приращение функции
соответствует приращение функции 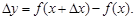
Производной функции y = f(x)в точке x называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю. Обозначение производной: 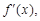 или
или 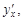 или
или 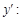
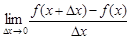 =
= 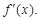
Операция нахождения производной называется дифференцированием. Функция y = f(x), которая имеет производную в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
Тест 1.Указать, какое из нижеперечисленных предложений определяет производную функции (когда приращение аргумента стремится к 0):
1) отношение приращения функции к приращению аргумента;
2) предел отношения функции к приращению аргумента;
3) отношение функции к пределу аргумента;
4) отношение предела функции к аргументу;
5) предел отношения приращения функции к приращению аргумента.
Теорема. Если функция y = f(x) в точке x имеет производную f ¢(x), то она непрерывна в этой точке.
Обратное утверждение неверно. Функция может быть непрерывна в точке, но не иметь в ней производной. Например, функция 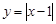 в точке x = 1 непрерывна, но не имеет в ней производной.
в точке x = 1 непрерывна, но не имеет в ней производной.
Геометрический смысл производной заключается в том, что производная функции y = f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.
Правила дифференцирования и таблица производных
Пусть 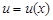 и
и 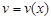 − две дифференцируемые в некотором интервале функции.
− две дифференцируемые в некотором интервале функции.
Теорема 1.Производная алгебраической суммы двух дифференцируемых функций равна алгебраической сумме производных этих функций
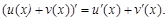
Теорема 2. Производная произведения двух дифференцируемых функций равна сумме произведений каждой функции на производную другой
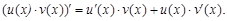
Следствие. Постоянный множитель можно выносить за знак производной
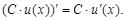
Теорема 3.Производную частного двух дифференцируемых функций можно найти по формуле
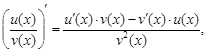
где 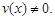
Все основные элементарные функции являются дифференцируемыми и имеют производные:
1) 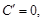 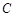 – постоянная; – постоянная; | 9) 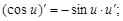 |
2) 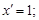 | 10) 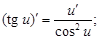 |
3) 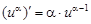 , , 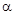 − постоянная; − постоянная; | 11) 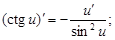 |
4) 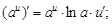 | 12) 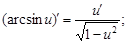 |
5) 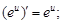 | 13) 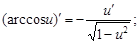 |
6) 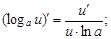 | 14) 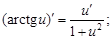 |
7) 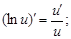 | 15) 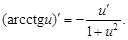 |
8) 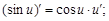 |
Пример 1.Найти производную функции 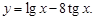
Решение
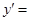
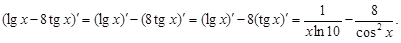
Пример 2.Найти производную функции 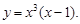
Решение
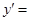
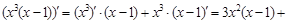
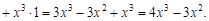
Пример 3. Найти производную функции 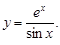
Решение
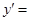
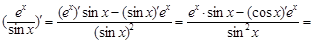
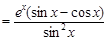 .
.
Тест 2. Производная функции 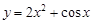 равна:
равна:
1) 2x + sin x;
2) x4 + sin x;
3) 4x – sin x;
4) 4x cos x + x2 sin x;
5) 2x – sin x.
Тест 3. Производная функции 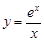 равна:
равна:
1) 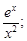
2) 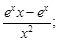
3) 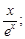
4) 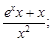
5) 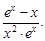
Производная сложной функции
Есть функция y = f(u), где и = j(x).
Функция, заданная формулой y = f(j(x)), называется сложной функцией.
Пример 4. Функция f(x) = 2x2+1 – сложная: f(u) = 2u, 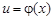 = x2 + 1.
= x2 + 1.
Если функция j(x) дифференцируема в точке x, а функция f(u) – в точке u = j(x), то сложная функция y = f(j(x)) тоже дифференцируема и справедлива теорема, представленная ниже.
Теорема. Производную сложной функции y = f(j(x)) можно найти по формуле
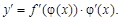
Пример 5. Найти производную функции 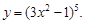
Решение
Пусть 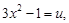 тогда
тогда 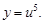
По теореме о производной сложной функции
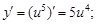
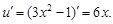
Тогда 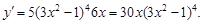
Тест 4.Производная функции 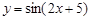 равна:
равна:
1) 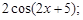
2) 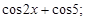
3) 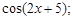
4) 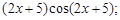
5)