Задания для самостоятельного решения. 1.1. Найдите полярные координаты точек A(1, 1), B C(–2, 2), D(0, 1)

I уровень

1.1. Найдите полярные координаты точек A(1, 1), B 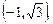C(–2, 2), D(0, 1), E(–3, 0), F(2, 0), G(0, –1), H(1, )

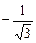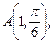
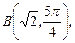
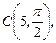
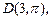
1.2. Зная полярные координаты точек 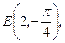найдите их прямоугольные координаты.

1.3. Уравнение линии на плоскости задано в прямоугольных координатах. Найдите их соответствующее уравнение в полярных координатах (полюс совпадает с началом прямоугольной системы координат, полярная ось – с осью абсцисс):

1) ρ = 2; 2) 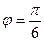; 3) ρ = 2sinφ.

1.4. Найдите уравнение линии в прямоугольной системе координат, если известны параметрические уравнения (исключить параметр):

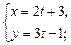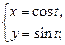1) 2) 3)

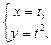
II уровень

2.1. Найдите полярные координаты точек, симметричных им относительно полярной оси

.

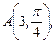
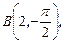
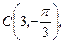
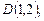
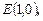
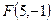2.2. Даны полярные координаты точек 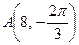и 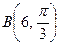. Вычислите полярные координаты середины отрезка АВ.

2.3. Определите, какую кривую на плоскости образуют точки, для которых расстояние от точки А(4, 0) вдвое больше расстояния от точки В(1, 0).

2.4. Найдите полярные уравнения фигур, если известны их уравнения в прямоугольной системе координат xOy:

1) 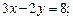2)

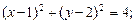
3)

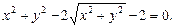
III уровень

3.1. Найдите уравнение кривой, состоящей из тех точек плоскости, разность расстояний от которых до точек F₁(–2, –2) и F₂(2, 2) равна 4.

3.2. Составьте параметрические уравнения окружности x² + y² – 2x = 0, приняв за параметр угол между осью Ox и прямой, проходящей через центр окружности.

3.3. Опишите с помощью уравнения в полярных координатах множество точек, лежащих на прямой, перпендикулярной полярной оси и проходящей через точку А(5, 0).

3.4. Уравнения кривых заданы в полярных координатах. Найдите их уравнения в соответствующих прямоугольных координатах:

1) ρ² = sinφ; 2) ρ = cosφ + sinφ;

3) ρ²cosφ sinφ = 1; 4) ρ² – 2 ρcosφ – 3 = 0.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

Прямая на плоскости

1. Положение прямой L на плоскости относительно прямоугольной системы координат xOy однозначно определено, если задан направляющий вектор 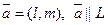и радиус-вектор 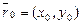некоторой фиксированной точки 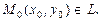В этом случае радиус-вектор 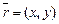произвольной точки 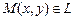задается формулой

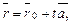(15)

где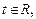

Уравнение (15) называется векторно-параметрическим уравнением прямой L.

2. Если 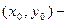координаты точки 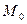, которая лежит на прямой 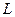, 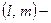координаты направляющего вектора, то прямая задается параметрическими уравнениями

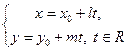
3. Если 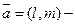направляющий вектор, такой, что 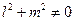, и 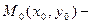точка, через которую проходит прямая, то верно каноническое уравнение:

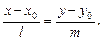(16)

4. Если L не параллельна Ox, то для всех направляющих векторов отношение 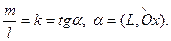По заданному угловому коэффициенту k прямой L и точке 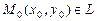уравнение прямой L может быть задано в следующем виде:

y – y₀ = k(x – x₀).

В случае, если M₀(0, b) – точка пересечения прямой L с осью Oy, это уравнение может быть записано так:

y = kx + b.

5. Координаты направляющего вектора 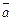прямой L могут быть найдены, если известны две точки M₀(x₀, y₀) и M₁(x₁, y₁) этой прямой: 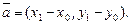Уравнение прямой, проходящей через две заданные точки:

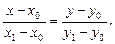(17)

6. Если известны точки пересечения прямой L с координатными осями, т. е. точки M₀(a, 0) и M₁(0, b), то справедливо уравнение «в отрезках»:

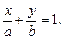
7. Положение прямой на плоскости однозначно определено и в случае, когда задан нормальный вектор 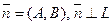этой прямой и точка 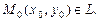Условие перпендикулярности векторов 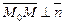позволяет перейти к векторному уравнению

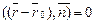
и затем к его координатной форме:

A(x – x₀) + + B(y – y₀) = 0 или

Ax + By + C = 0, (18)

где C = –Ax₀ – By₀.

Уравнение (18) называется общим уравнением прямой L.

8. Если в качестве нормального вектора берется единичный вектор 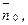направленный из начала координат в сторону прямой, т.е.

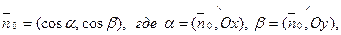
то справедливо нормальное уравнение прямой L на плоскости:

xcosα + ycosβ – p = 0,

где p > 0 – расстояние от начала координат до прямой.

Величина δ(M₀, L) = x₀cosα + y₀cosβ – p, где 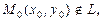называется отклонением точки М₀ от прямой L. При этом δ < 0, если M₀ и O(0, 0) лежат по одну сторону от прямой L, δ > 0 – если по разные. Расстояние d(M₀, L) от точки до прямой равно абсолютному значению отклонения.

От общего уравнения прямой к нормальному можно перейти с помощью умножения на нормирующий множитель

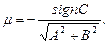
Расстояние от точки M₀(x₀, y₀) до прямой L: Ax + By + C = 0 может быть найдено по формуле:

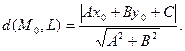(19)

Угол между прямыми может быть найден с помощью косинуса угла между их направляющими или нормальными векторами, а также по формуле:

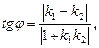
где k₁ и k₂ – угловые коэффициенты прямых.

При этом возможны частные случаи:

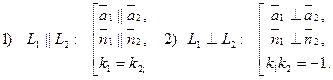
Здесь L₁ и L₂ – прямые на плоскости, для которых 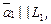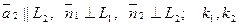– угловые коэффициенты соответственно прямых 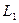и .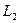

В полярной системе координат уравнение прямой имеет вид

ρcos(φ – φ₀) = p,

где p – длина перпендикуляра, проведенного из полюса к прямой, φ₀ – угол между полярной осью и перпендикуляром.

Пример 1. Даны вершины треугольника ABC: A(1, 2), B(–1, –3), C(2, –1). Найти:

1) уравнение прямой BC;

2) уравнение высоты AH и ее длину;

3) уравнение медианы BM;

4) угол между прямыми BM и AH;

5) уравнения биссектрис внутреннего и внешнего угла при вершине А.

Решение. 1. Для составления уравнения прямой BC воспользуемся заданными координатами точек B, C и уравнением прямой, проходящей через две заданные точки (17). Так как B(–1, –3), C(2, –1), имеем:

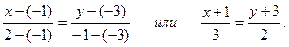
Последнее уравнение приведем к общему уравнению, использовав основное свойство пропорции:

2(x + 1) = 3(y + 3) или 2x – 3y – 7 = 0.

Таким образом, окончательно получаем:

2x – 3y – 7 = 0.

2. Для построения уравнения высоты АН воспользуемся условием перпендикулярности прямых AH и ВС: нормальным вектором прямой ВС является 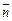=(2; –3), т.е.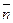 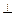ВС . Этот вектор можно рассматривать как направляющий вектор прямой АН. Значит, каноническое уравнение прямой AH, согласно (16), имеет вид:

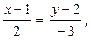(20)

где А(1, 2) 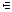АН.

Чтобы найти длину высоты АВС, опущенную из вершины А, воспользуемся формулой расстояния (19):

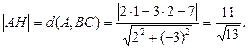
3. Для составления уравнения медианы ВМ найдем координаты точки М, являющейся серединой отрезка AC:

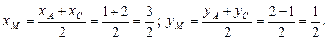
Получаем M(3/2, 1/2). Запишем уравнение прямой BM по двум известным точкам B(–1, –3) и M(3/2, 1/2), используя формулу (17):

.

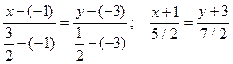Если приводить его к общему уравнению, получим

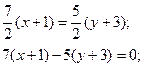
7x – 5y – 8 = 0.

4. Угол φ между прямыми BM и AH найдем, используя угол между их нормальными векторами

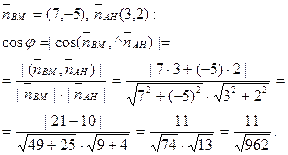
Получаем .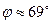

5. Пусть точка M(x, y) лежит на биссектрисе AB. Тогда по свойству биссектрисы d(M, AB) = d(M, AC). Запишем уравнения прямым. Получаем

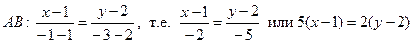Получаем

.

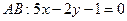Аналогично,

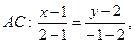
т.е. .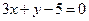

Используем формулу расстояния (19):

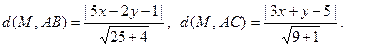
Значит,

.

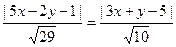По основному свойству пропорции и свойству модуля имеем

.

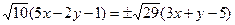Итак, получили две биссектрисы (внутреннего и внешнего углов при вершине А):

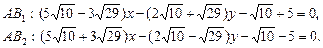
Пример 2. Даны две точки A(–3, 8) и B(2, 2). На оси Ox найти такую точку M, сумма расстояний от которой до двух заданных точек была бы наименьшей.

Решение. Воспользуемся утверждением, смысл которого состоит в следующем: наименьшее расстояние между двумя точками достигается в случае движения по прямой. Тогда задача будет заключаться в поиске точки пересечения прямой AB¢ (рис. 11) с осью Ox, где B¢ – точка, симметричная точке В относительно оси Ox (или в нахождении точки пересечения прямой A¢B с осью Ox, где A¢ – точка, симметричная А относительно Ox).

Рис. 11

Точки B¢(2, –2) и A(–3, 8) определяют прямую AB¢:

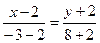, т.е. 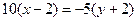или .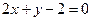

Значит, для нахождения координат искомой точки М осталось решить систему уравнений: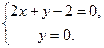

Решаем ее:

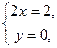
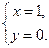
Итак, точка М(1, 0) является искомой.