Охлаждение полубесконечного стержня и стержня ограниченных размеров

Краевая задача для полубесконечного стержня:

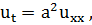
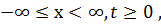(3.4 a)

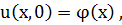
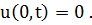
Левый край стержня поддерживается при нулевой температуре.

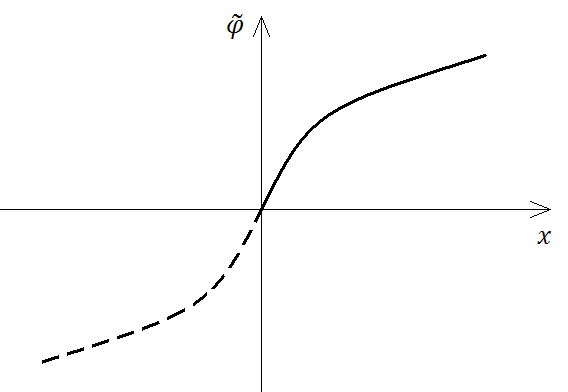Введем вместо новую функцию :

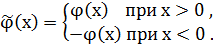
При таком продолжении задача (3.4а) сводится к (3.2), решение которой имеет вид формулы Пуассона:

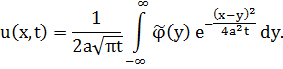
Рис. 20

В параграфе 3.2 было показано, что данная функция удовлетворяет дифференциальному уравнению и начальным условиям: 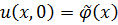. Нужно доказать, что выполняется краевое условие.

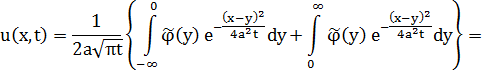
(во втором интеграле заменим y на –y)

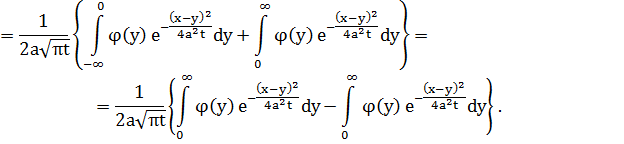
При 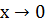эти два интеграла совпадают, т.е. 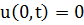. Ч.т.д.

Теперь рассмотрим тот же стержень при условии отсутствия теплопередачи через левый край:

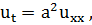
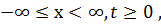(3.4 б)

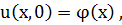
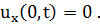
Введем новую функцию 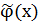такую, что:

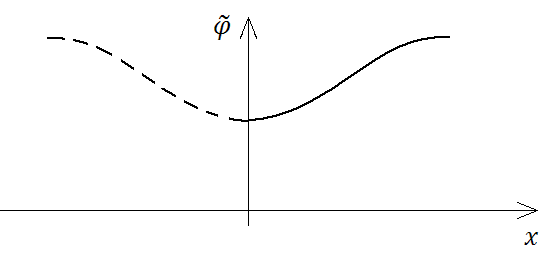
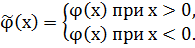
Рис. 21

Задача (3.4б) сводится к задаче (3.2) и имеет решение (3.3):

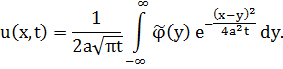
Проверим выполнимость краевого условия:

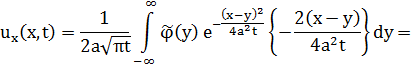
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>=</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">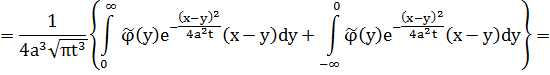

(во втором интеграле заменим y на –y)

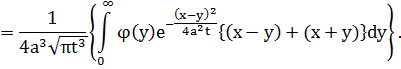
При 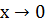это выражение равно 0, т.е. .

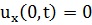Ч.т.д.

Рассмотрим охлаждение стержня ограниченных размеров, оба конца которого имеют нулевую температуру.

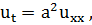
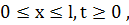(3.5)

Продолжим начальное условие нечетным образом влево и вправо с периодом 2l.

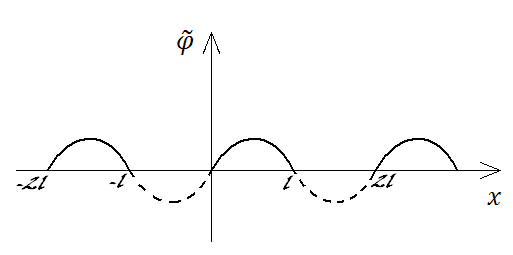
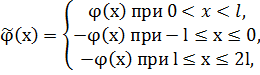
и т.д.

Рис. 22

Тогда задача (3.5) сводится к (3.2) и дает решение в виде формулы Пуассона:

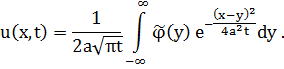
Уже было показано, что эта функция удовлетворяет уравнению теплопроводности и начальному условию 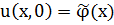при выполнении условия Липшица.

Проверим выполнение краевого условия 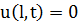. Для этого разобьем интеграл на два:

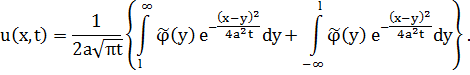
Введем новую переменную z=y-l

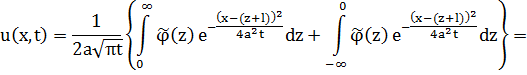
Заменим z на –z во втором интеграле.

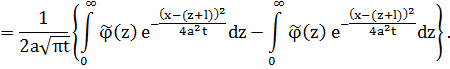
Если x=l, то

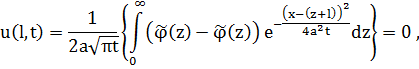
Ч.т.д.

3. 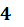. Решение неоднородной краевой задачи теплопроводности.

Задача для бесконечного стержня с подкачкой в него энергии будет иметь вид

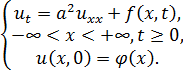(3.6)

В данной задаче подкачку энергии определяет функция .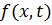

Представим решение в виде суммы слагаемых (метод редукции):

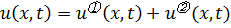, и для каждого слагаемого составим свои задачи (3.6a) и (3.6б).

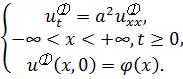(3.6a)

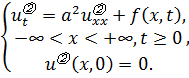(3.6б)

Задача (3.6a) это задача (3.2), то есть ранее уже решенная. Её решение представляется формулой Пуассона:

.

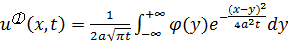Будем искать решение задачи (3.6б) в виде

.

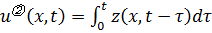Лемма:

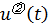– удовлетворяет (3.6б), если 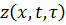удовлетворяет (3.6в)

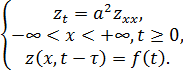(3.6в)

Доказательство:

Найдем 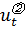и :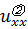

.

.

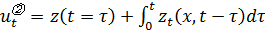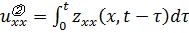Можно увидеть, что

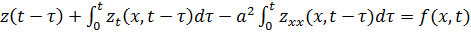, т.е. .

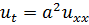Лемма доказана.

Найдем решение (3.6в).

Введем новую переменную 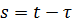и функцию 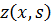, тогда (3.6в) примет вид

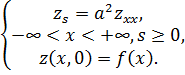
Это задача является задачей (3.2) с заменами 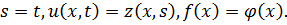Её решение имеет вид (3.3):

.

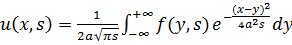Поскольку ,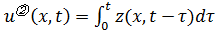

.

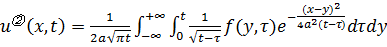В конечном итоге получаем решение

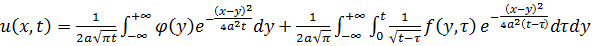
(3.7)

При 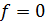подкачки энергии нет, решение (3.7) принимает вид решения (3.3).

3. . Решение однородной краевой задачи теплопроводности методом разделения переменных

Вернемся к задаче охлаждения стержня ограниченных размеров (3.5).

Оба края стержня находятся при фиксированной нулевой температуре.

Представим искомую функцию, в виде

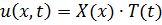и подставим в дифференциальное уравнение.

,

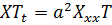Разделим переменные:

.

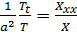Левая часть зависит только от 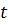, а правая только от 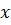. Такое возможно, только если обе части одна и та же константа. Если эта константа отрицательна, то решение для 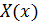есть, если константа положительная или равна нулю, то решения нет. Это было доказано в теме 2.

Обозначим

.

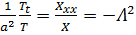Для функци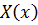й и 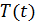получаем уравнения

,

.

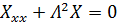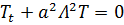Построим краевые задачи для этих функций.

Для функции :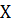

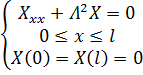
Найдем решение этой задачи:

,

,

.

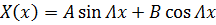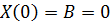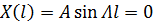Если 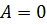, то решение будет нулевое, оно нас не интересует, значит,

→ .

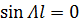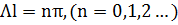Получаем дискретный набор 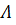(собственных значений):

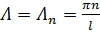, ему соответствует дискретный набор собственных функций:

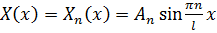, где 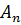произвольная константа.

Пользуясь произвольностью выбора 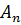, положим что 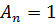, в таком случае получаем

.

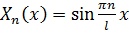Для функции T: .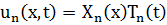

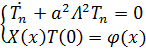
Решение дифференциального уравнения имеет вид

.

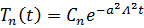Найдем 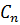из начальных условий:

Пусть 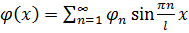, где .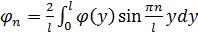

Тогда

,

.

.

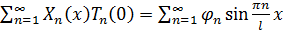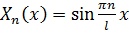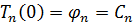Нашли частное решение в виде

.

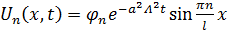Чтобы найти общее решение, построим бесконечный ряд

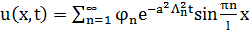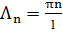, где (3.8)

Чтобы ряд (3.8) был общим решением задачи (3.5),надо чтобы ряды для 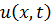, , 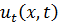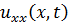равномерно сходились.

,

.

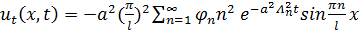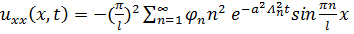Чтобы ряды равномерно сходились, надо чтобы сходились мажорантные ряды:

,

,

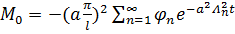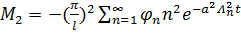Будем считать, что 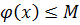, то есть начальная температура ограничена сверху:

.

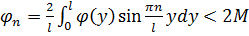Нас интересуют ряды: 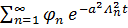и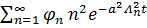

Проверим их сходимость.

Условие сходимости ряда .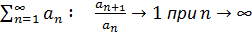

Применим его для наших рядов:

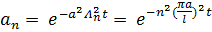, возьмем 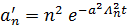и рассмотрим отношение:

.

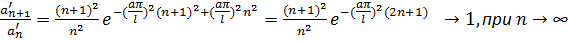Мы доказали сходимость мажорантных рядов, значит,равномерно сходятся ряды для 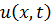, , 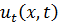, 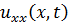а значит (3.8) является общим решением задачи (3.5).

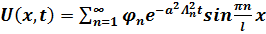, где 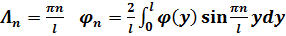.(3.8)

3. . Решение неоднородной краевой задачи теплопроводности методом разделения переменных

Задача на подогрев стержня ограниченных размеров имеет вид

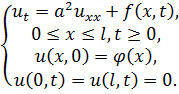(3.9)

Представим её решение в виде суммы решений (метод редукции):

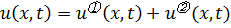, и для каждого решения составим свои задачи.

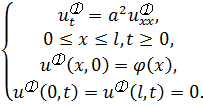(3.9a)

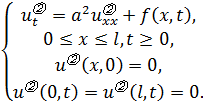(3.9б)

Задача (3.9a) ранее уже решена. Её решением является:

.

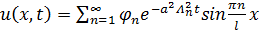Будем искать решение задачи (3.9б). Представим функцию 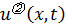в виде ряда

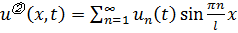, чтобы сразу удовлетворить краевым условиям.

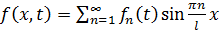, где

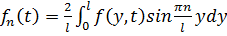. После подстановки получим:

.

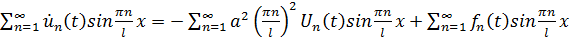Приравниваем коэффициенты при одинаковых гармониках и получаем дифференциальное уравнение:

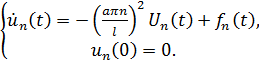(3.9в)

Решение будем искать в виде

.

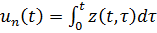Покажем, что

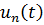- удовлетворяет (3.9в),если 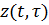- удовлетворяет (3.9г).

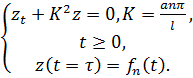(3.9г)

Доказательство:

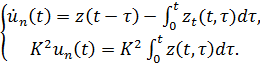
Складывая оба уравнения системы получим

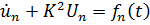.Лемма доказана.

Осталось найти решение (3.9г).

Введем переменную 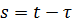. . 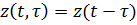Получаем измененное условие задачи (3.9г):

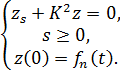
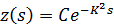, t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> .

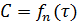Подставим в 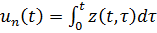, получим:

,

,

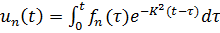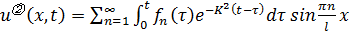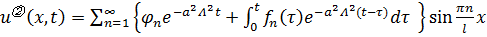. (3.10)

При 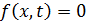(3.10) сводится к (3.8).

3. . Существование, единственность и корректность решений краевых задач теплопроводности

Существование решений различных краевых задач теплопроводности было доказано в рамках данной темы 3.

1. Докажем единственность решения общей краевой задачи.

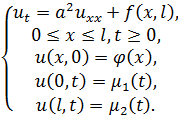
Доказательство проведём от противного: предположим, что есть 2 разных решения этой краевой задач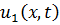и, и .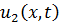

Построим функцию 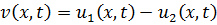. Поставим для неё краевую задачу

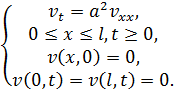
Решение этой краевой задачи в соответствие с теоремой об экстремуме является нулевым, значит,

.

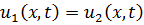2. Вернемся к задаче на охлаждение бесконечного стержня.

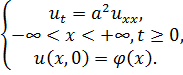При доказательстве будем считать 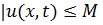во всей области определения решения.

Исходя от противного предположим, что есть два разных решения 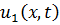и 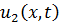. Получаем ограничение для функции .

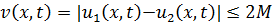Временно ограничим координату 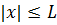и введем функцию 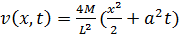, которая удовлетворяет уравнению теплопроводности.

Поскольку 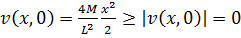, , 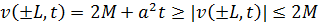получаем 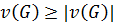и на основе следствия 3 из теоремы об экстремуме .

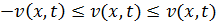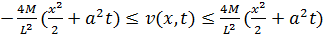. Устремляем 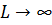и получаем

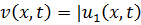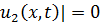- . Следовательно, .

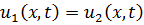3.Краевую задачу будем называть корректной, если малому изменению начальных или краевых условий соответствует малое изменение её решения. Рассмотрим 2 краевые задачи, отличающиеся малым изменением начальных и краевых условий.

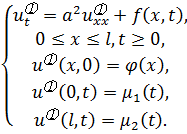
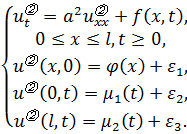
Построим функцию 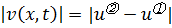, для которой получим:

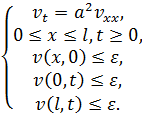
Здесь в качестве 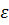выбрано наибольшее из 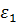, , 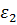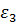. Видим, что на границе области 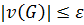. В соответствие со следствием 3 получаем 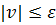во всей области определения решения. Следовательно, 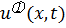мало отличается от .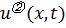