Базисы в линейном пространстве

Упорядоченный набор векторов

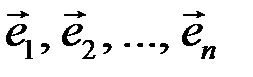(5.5)

линейного пространства 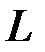образуют базис в 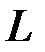, если

1) векторы (5.5) линейно независимы,

2) любой вектор 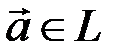можно представить в виде линейной комбинации векторов (5.5):

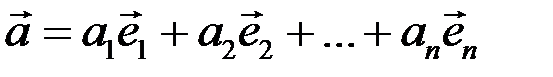. (5.6)

Равенство (5.6) называется разложением вектора 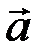по базису (5.5). Для каждого вектор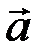а числа 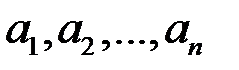определяются однозначно; они называются координатами вектора 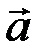в базисе (5.5).

При фиксированном базисе соответствие между векторами 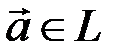и их координатными строками – арифметическими векторами 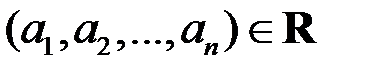взаимно-однозначно: каждому вектору соответствует единственная строка, разным векторам – разные строки. Как и в случае геометрических векторов, при сложении двух векторов их координатные строки складываются, при умножении на число – умножаются на это число. Вышесказанное позволяет при выполнении линейных операций фактически отождествить вектор 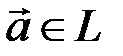с его координатной строкой и писать .

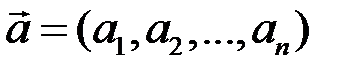Линейные пространства, в которых существует базис, называются конечномерными. Можно показать, что любой базис в конечномерном линейном пространстве 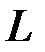содержит одно и то же число векторов. Это число 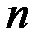называется размерностью линейного пространства 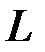; говорят, что 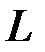– 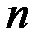-мерное линейное пространство и обозначают его с указанием размерности: .

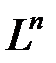Согласно п. 5.1.5 линейное пространство 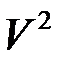геометрических векторов на плоскости двумерно, линейное пространство 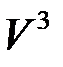геометрических векторов в пространстве трехмерно. Пространство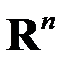 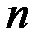-мерно.

Линейное пространство, в котором существует любое число линейно независимых векторов и потому не существует базиса, называется бесконечномерным. Например, бесконечномерным является линейное пространство 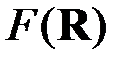всех функций на (см. задачу 5.3.20).

Примеры решения задач

5.2.1.

Рис. 5.4

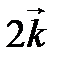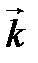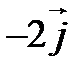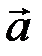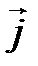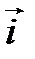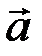Вектор задан координатами в ортонормированном базисе 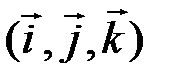: 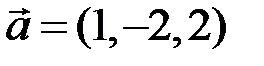. Записать разложение 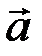по этому базису и изобразить его на рисунке.

◄ Разложение вектора 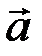по базису 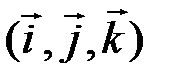имеет вид 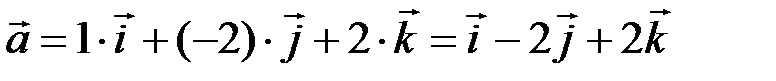(рис. 5.4). ►

5.2.2.Даны векторы 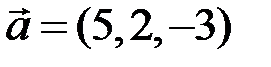и 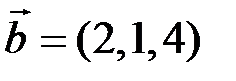. Найти , , .

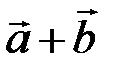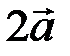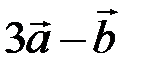◄ Задание можно понимать двояко. 1) В некотором базисе 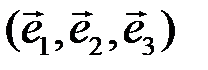заданы координаты геометрических векторов 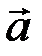и 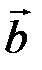. Надо найти координаты указанных векторов в том же базисе. 2) Заданы арифметические векторы – строки из 3 чисел и надо сделать с ними указанные операции. Наши действия в обоих случаях одинаковы – используем формулы (5.2):

, ,

. ►

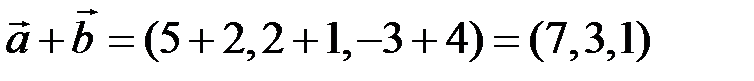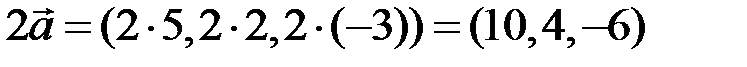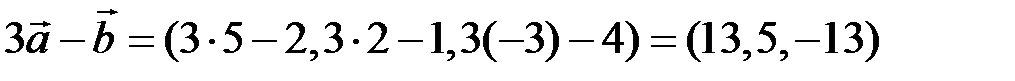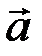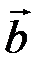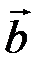5.2.3.Коллинеарны ли векторы и , и 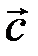, если

, , .

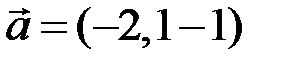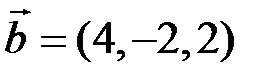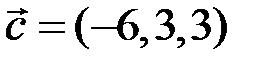◄ Координаты векторов 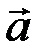и 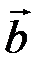пропорциональны: 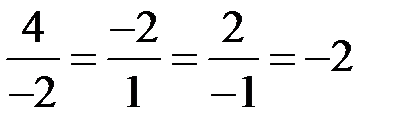. Следовательно, 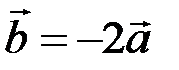или в более симметричной записи 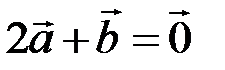, то есть векторы 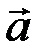и 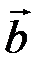линейно зависимы и потому коллинеарны: .

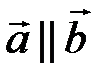Координаты векторов 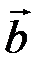и 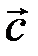не пропорциональны: 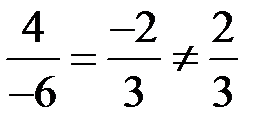. Поэтому векторы 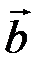и 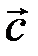не коллинеарны (линейно независимы). ►

5.2.4.Убедиться, что векторы 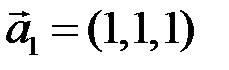, , 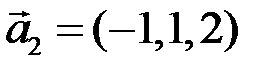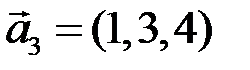линейно зависимы. Найти эту зависимость. Является ли вектор 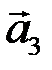линейной комбинацией векторов 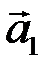и ?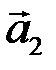

◄ Мы должны показать, что векторы 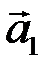, , 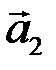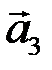удовлетворяют соотношению (5.1): 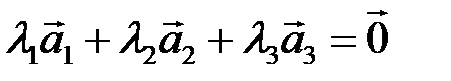, где хотя бы одно 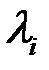отлично от нуля.

Из (5.2) следует, что в координатах это равенство имеет вид

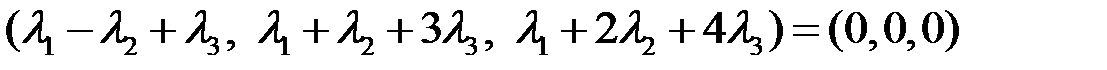
или

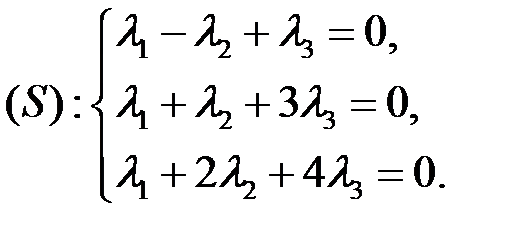
Решаем эту систему методом Гаусса.

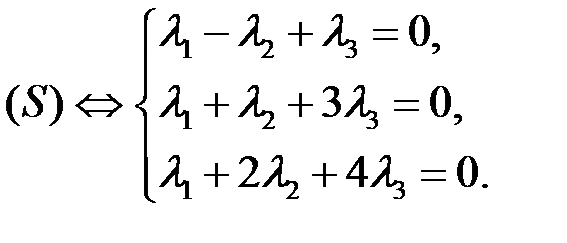
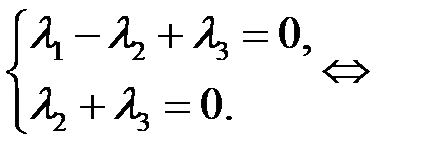
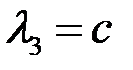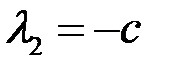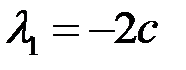, , , где .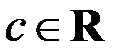

Для определенности возьмем 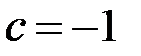. Тогда 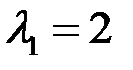, , 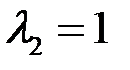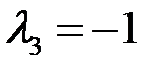. Таким, образом, показано, что векторы 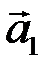, , 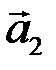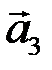линейно зависимы, и эта зависимость имеет вид 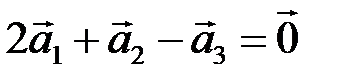. Любой из векторов 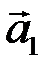, , 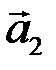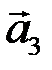можно представить в виде линейной комбинации остальных векторов. В частности, . ►

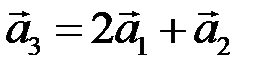5.2.5.Компланарны ли векторы , , ?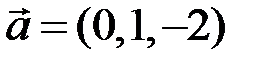

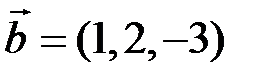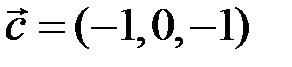◄ Компланарность трех векторов равносильна их линейной зависимости. Поскольку вид линейной зависимости, если она существует, нас не интересует, то удобно не использовать непосредственно определение линейной зависимости, как в задаче 5.2.4, а ограничиться проверкой условия компланарности векторов в форме (5.4):

,

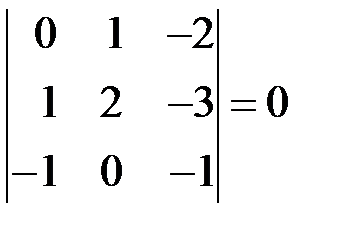Следовательно, векторы 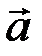, , 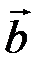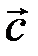компланарны. ►

5.2.6.1) Убедиться, что векторы 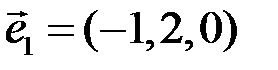, , 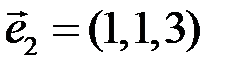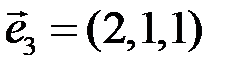образуют базис; 2) разложить вектор 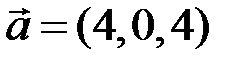по этому базису.

◄ 1) Так как 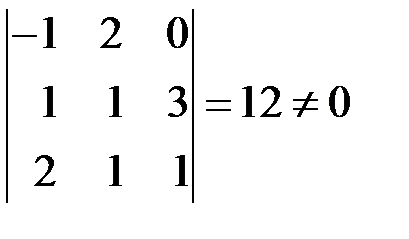, то векторы 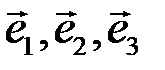линейно независимы (некомпланарны) и образуют базис;

2) разложение вектора 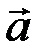по базису 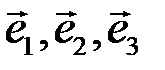имеет вид 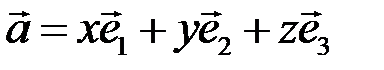. Это векторное равенство в координатной форме равносильно системе линейных уравнений:

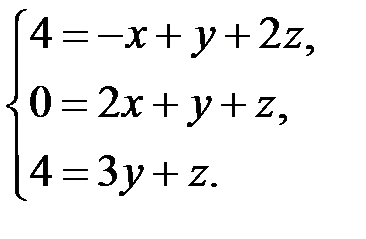
Решая эту систему, получаем 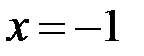, , 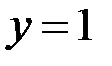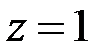. Значит, . ►

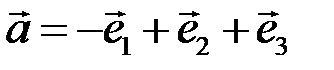5.2.7.Доказать, что множество 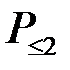всех многочленов от одной переменной степени 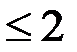с «обычными» операциями сложения и умножения на действительное число является линейным пространством. Найти его базис. Доказать, что множество всех многочленов второй степени, то есть квадратных трехчленов, не является линейным пространством.

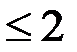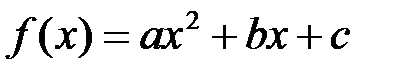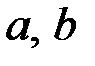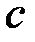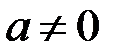
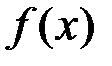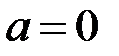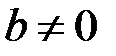
◄ 1. Многочлен степени имеет вид , где коэффициенты и – действительные числа. При – многочлен второй степени, при , 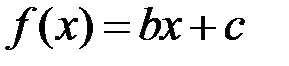– многочлен первой степени, при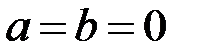 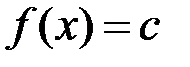– многочлен нулевой степени.

2. Произведение многочлена 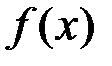на число 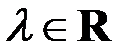– также многочлен 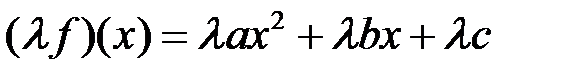степени .

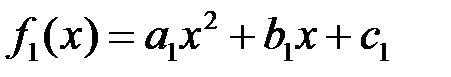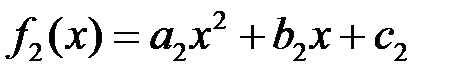Сумма многочленов и – многочлен 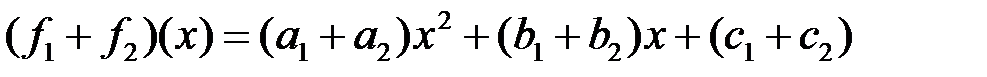, степень которого не превышает 2. Свойства 1-8 из определения линейного пространства очевидно выполняются. Роль нулевого вектора играет нулевой многочлен 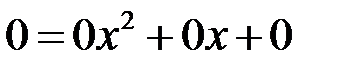, многочлен, противоположный имеет вид 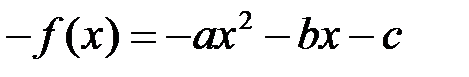. Таким образом, множество 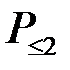всех многочленов степени 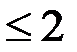с определенными выше операциями суммы и произведения на число является линейным пространством.

3. Покажем, что многочлены 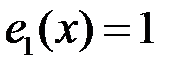, , 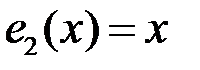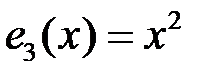образуют базис линейного пространства 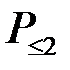. Проверим их линейную независимость. Равенство (5.1) в нашем случае имеет вид 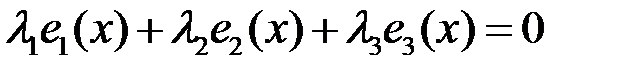для всех 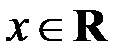, то есть 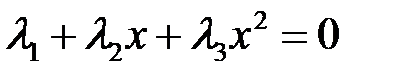для всех 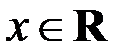. Так как уравнение степени 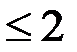с ненулевыми коэффициентами имеет не более двух корней, то это равенство возможно только при 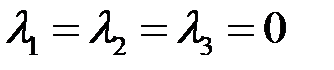. Это означает, что многочлены 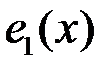, , 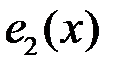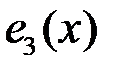– линейно независимы. Очевидно, что любой многочлен 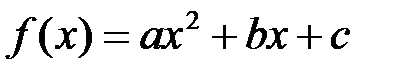– их линейная комбинация:

.

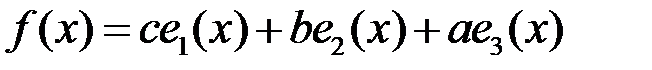4. Операции над многочленами второй степени могут дать многочлен меньшей степени. Например, произведение числа 0 на многочлен второй степени равно нулю, сумма многочлен второй степени с противоположным многочленом также нуль, а нуль – многочлен нулевой степени. Поэтому множество многочленов второй степени не является линейным пространством. ►