Функциональные последовательности
Определение. Если членами ряда являются функции переменой х, то ряд называется функциональным.
Исследование на сходимость функциональных рядов сложнее исследования числовых рядов. Один и тот же функциональный ряд может при одних значениях переменной х сходиться, а при других – расходиться. Поэтому вопрос сходимости функциональных рядов сводится к определению тех значений переменной х, при которых ряд сходится.
Совокупность таких значений называется областью сходимости.
Так как пределом каждой функции, входящей в область сходимости ряда, является некоторое число, то пределом функциональной последовательности будет являться некоторая функция:
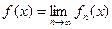
Определение. Говорят, что функциональная последовательность 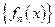 сходится к функции
сходится к функции 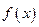 на отрезке
на отрезке 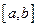 , если для любого числа
, если для любого числа 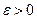 и любой точки х из рассматриваемого отрезка существует номер
и любой точки х из рассматриваемого отрезка существует номер 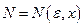 , такой, что неравенство
, такой, что неравенство
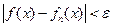
выполняется при 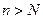 .
.
При выбранном значении 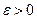 каждой точке отрезка
каждой точке отрезка 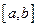 соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка
соответствует свой номер и, следовательно, номеров, соответствующих всем точкам отрезка 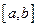 , будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка
, будет бесчисленное множество. Если выбрать из всех этих номеров наибольший, то этот номер будет годиться для всех точек отрезка 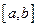 , т.е. будет общим для всех точек.
, т.е. будет общим для всех точек.
Определение. Говорят, что функциональная последовательность 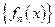 равномерно сходится к функции
равномерно сходится к функции 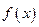 на отрезке
на отрезке 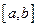 , если для любого числа
, если для любого числа 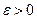 существует номер
существует номер 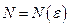 , такой, что неравенство
, такой, что неравенство
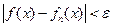
выполняется при 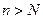 для всех точек отрезка
для всех точек отрезка 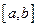 .
.
Пример. Рассмотрим последовательность 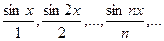
Данная последовательность сходится на всей числовой оси к функции 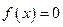 , т.к.
, т.к.
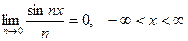 .
.
Построим графики этой последовательности:
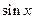
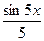

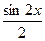
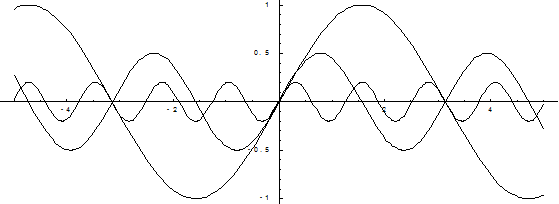
При увеличении числа n график последовательности приближается к оси х.
Функциональные ряды
Определение. Частичными суммами функционального ряда 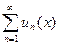 называются функции
называются функции 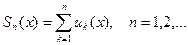
Определение. Функциональный ряд 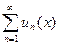 называется сходящимся в точке
называется сходящимся в точке 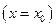 , если в этой точке сходится последовательность его частных сумм. Предел последовательности
, если в этой точке сходится последовательность его частных сумм. Предел последовательности 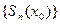 называется суммой ряда
называется суммой ряда 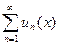 в точке
в точке 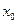 .
.
Определение. Совокупность всех значений х, для которых сходится ряд 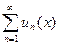 называется областью сходимостиряда.
называется областью сходимостиряда.
Определение. Ряд 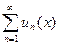 называется равномерно сходящимся на отрезке
называется равномерно сходящимся на отрезке 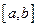 , если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
, если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда). Для равномерной сходимости ряда 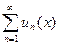 необходимо и достаточно, чтобы для любого числа
необходимо и достаточно, чтобы для любого числа 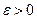 существовал такой номер
существовал такой номер 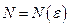 , что при
, что при 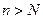 и любом целом
и любом целом 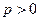 неравенство
неравенство
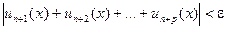
выполнялось бы для всех х на отрезке 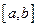 .
.
Теорема. (Признак равномерной сходимости Вейерштрасса) Ряд 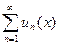 сходится равномерно и абсолютно на отрезке
сходится равномерно и абсолютно на отрезке 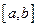 , если модули его членов на этом же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами:
, если модули его членов на этом же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами:
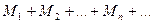
т.е. имеет место неравенство:
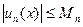 .
.
При этом говорят, что в этом случае функциональный ряд 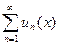 мажорируетсячисловым рядом
мажорируетсячисловым рядом 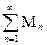 .
.
Пример. Исследовать на сходимость ряд 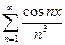 .
.
Так как 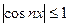 всегда, то очевидно, что
всегда, то очевидно, что 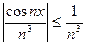 .
.
При этом известно, что обобщённый гармонический ряд 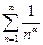 при
при 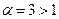 сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.
сходится, то в соответствии с признаком Вейерштрасса исследуемый ряд равномерно сходится и притом в любом интервале.
Пример. Исследовать на сходимость ряд 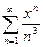 .
.
На отрезке 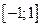 выполняется неравенство
выполняется неравенство 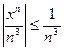 т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах
т.е. по признаку Вейерштрасса на этом отрезке исследуемый ряд сходится, а на интервалах 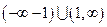 , расходится.
, расходится.
