Тема 3: Абсолютные, относительные и средние величины. Показатели вариации.
Относительные величины образуют систему взаимосвязанных статистических показателей. По содержанию выражаемых количественных соотношений выделяют следующие типы относительных величин.
Относительный показатель динамики. Характеризует изменение уровня развития какого-либо явления во времени. Получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент.
Текущий уровень
 ОПД =
ОПД =
Предшествующий или базисный уровень
Относительный показатель плана. Рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде.
Уровень, планируемый на (i+1)-ый период
 ОПП =
ОПП =
Уровень, достигнутый в i-ом периоде
Относительный показатель реализации плана. Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному.
Уровень, достигнутый в (i+1)-ом периоде
 ОПРП =
ОПРП =
Уровень, планируемый на (i+1)-ый период
Между этими показателями существует взаимосвязь: ОПП * ОПРП = ОПД
Относительный показатель структуры. Характеризуют доли, удельные веса составных элементов в общем итоге. Как правило, их получают в форме процентного содержания:
Показатель, характеризующий часть совокупности
 ОПС =
ОПС =
Показатель по всей совокупности в целом
Относительный показатель координации. Характеризуют отношение частей данной совокупности к одной их них, принятой за базу сравнения. ОПК показывают, во сколько раз одна часть совокупности больше другой, либо сколько единиц одной части приходится на 1, 10, 100, 1000, … единиц другой части. Относительные величины координации могут рассчитываться и по абсолютным показателям, и по показателям структуры.
Показатель, характеризующий i-ую часть совокупности
 ОПК =
ОПК =
Показатель, характеризующий часть совокупности,
выбранную за базу сравнения
Относительный показатель интенсивности. Характеризуют степень распределения или развития данного явления в той или иной среде. Представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком.
Показатель, характеризующий явление А
 ОПК =
ОПК =
Показатель, характеризующий среду распространения явления А
Относительный показатель сравнения. Характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям.
Показатель, характеризующий объект А
 ОПСр =
ОПСр =
Показатель, характеризующий объект Б
Средняя величина – это обобщающий показатель, характеризующий типический уровень явления. Он выражает величину признака, отнесенную к единице совокупности.
Средние величины делятся на два больших класса: степенные средние и структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая. В качестве структурных средних рассматриваются мода и медиана.
Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | ||
| Простая | Взвешенная | |||
| Гармоническая | -1 | 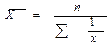 | 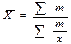 m = xf m = xf | |
| Геометрическая | 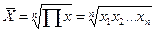 | 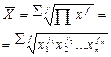 | ||
| Арифметическая | 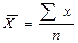 | 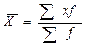 | ||
| Квадратическая | 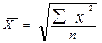 | 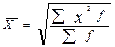 | ||
| Кубическая | 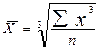 | 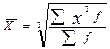 |
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы – величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Для интервального ряда расчет моды и медианы проводится по следующим формулам.
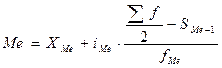 ,
,
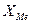 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
iMe- его величина;
Σf/2  - половина суммы частот;
- половина суммы частот;
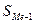 - сумма накопленных частот, предшествующая медианному интервалу;
- сумма накопленных частот, предшествующая медианному интервалу;
fMe- число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении).
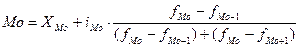 ,
,
где XMo- нижнее граница модального интервала;
fMo- частота модального интервала;
fMo- частота интервала, предшествующего модальному;
fMo- частота интервала, следующего за модальным;
iMo – величина модального интервала.
Для измерения вариации в статистике применяют несколько способов.
Наиболее простым является расчет показателя размаха вариации R как разницы между максимальным (Xmax) и минимальным (Xmin) наблюдаемыми значениями признака: 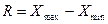 .
.
Более строгими характеристиками являются показатели колеблемости относительно среднего уровня признака. Простейший показатель такого типа – среднее линейное отклонение d как среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:
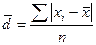 - невзвешенное среднее линейное отклонение,
- невзвешенное среднее линейное отклонение,
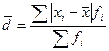 - взвешенное среднее линейное отклонение
- взвешенное среднее линейное отклонение
Дисперсия признака ( 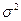 ) определяется на основе квадратической степенной средней:
) определяется на основе квадратической степенной средней:
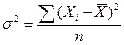 или
или 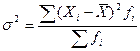 .
.
Показатель s, равный 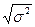 , называется средним квадратическим отклонением.
, называется средним квадратическим отклонением.
Если первичные данные сгруппировать, то дисперсия признака может быть определена как сумма так называемой межгрупповой дисперсии – δ2 и среднего значения внутригрупповых - 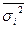 , т.е.
, т.е.
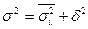 .
.
Mежгрупповая дисперсия рассчитывается как
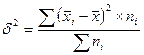 ,
,
где 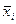 - среднее значение признака по группе i;
- среднее значение признака по группе i;
ni – численность группы i;
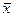 - общее среднее значение признака.
- общее среднее значение признака.
Средняя из внутригрупповых дисперсий рассчитывается по формуле
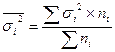 ,
,
где 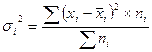 - групповая дисперсия.
- групповая дисперсия.
При расчете относительных показателей вариации базой для сравнения служит средняя арифметическая. Эти показатели дают характеристику однородности совокупности. К ним относятся:
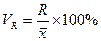 - коэффициент осцилляции,
- коэффициент осцилляции,
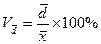 - линейный коэффициент вариации,
- линейный коэффициент вариации,
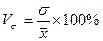 - коэффициент вариации.
- коэффициент вариации.
Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
