Устойчивость систем с запаздыванием

Иногда отдельные звенья САУ обладают «чистым» запазды­ванием, которое проявляется в том, что система реагирует на входной сигнал не сразу, а по истечении некоторого постоянного времени :

y(t) = x(t – τ), (7.1)

где τ – постоянная величина, называемая временем запаздывания.

Такие звенья называют запаздывающими, т.к. они воспроизводят изменения входной величины без искажения, но с некоторым τ. Например, таким звеном можно описать работу транспортера: на один конец которого поступает какой-то груз, а с другого конца этот груз принимают через промежуток времени τ . ПФ запаздывающего звена описывается

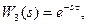(7.2)

Системы, содержащее хотя бы одно запаздывающее звено, называют системой с запаздыванием. Структурная схема таких систем может иметь два вида: запаздывающее звено (ЗЗ) находится в прямой цепи и в цепи обратной связи (рисунок 7.3).

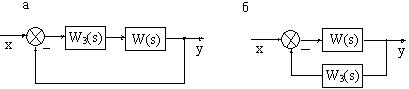
Рисунок 7.3 – Структурные схемы САУ с запаздыванием

ПФ разомкнутой системы с запаздыванием равна

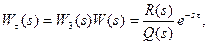(7.3)

где W(s)=R(s)/Q(s) – ПФ разомкнутой системы без запаздывания.

Если запаздывающее звено находится в прямой цепи (рисунок 7.3,а), то ПФ замкнутой системы равна

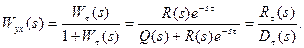(7.4)

Если запаздывающее звено находится в цепи обратной связи, то ПФ замкнутой системы равна

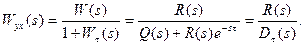(7.5)

Сопоставляя (7.4) и (7.5), видно, что независимо от места включения запаздывающего звена, характеристическое уравнение замкнутой системы равно

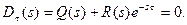(7.6)

Раскладывая показательную функцию в ряд Тейлора, получим

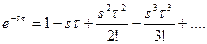
Тогда (7.6) можно рассматривать как уравнение «бесконечной степени», имеющее бесконечное число корней. Для устойчивости системы необходимо, чтобы все корни характеристического уравнения (8.6) были левыми. Очевидно, что алгебраические критерии Рауса и Гурвица для исследования устойчивости систем с запаздыванием непригодны. Для этого можно использовать только частотные критерии Михайлова и Найквиста либо метод Д-разбиения.

Использование критерия Михайлова нецелесообразно ввиду сложности построения. Поэтому рекомендуется применять критерий Найквиста: устойчивость замкнутой системы с запаздыванием определяется по поведению АФЧХ W_τ(jω) разомкнутой системы (3.3) с запаздыванием относительно точки (-1,j0). Подставляя s = jω в (8.3), получим АФЧХ W_τ(jω) разомкнутой системы

с запаздыванием

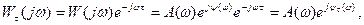(7.7)

где

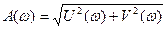- амплитудно-частотная характеристика АЧХ;

ψ(ω) = arctg (V/U) – фазо-частотная характеристика ФЧХ разомкнутой системы без запаздывания;

ψ_τ(ω) = ψ(ω) – ω_τ (7.8)

ФЧХ разомкнутой системы с запаздыванием.

Из (8.7) и (8.8) видно, что наличие запаздывающего звена не меняет модуль А(ω) АФЧХ разомкнутой системы W(jω), а вносит лишь дополнительный фазовый сдвиг ω_τ , пропорциональный частоте, при чем коэффициентом пропорциональности является время запаздывания τ.

Для построения АФЧХ W_τ(jω) разомкнутой системы с запаздыванием нужно каждый модуль А(ω_i) вектора АФЧХ W(jω) разомкнутой системы без запаздывания повернуть на угол ωiτ по часовой стрелке. С ростом частоты ω угол ω_τ будет быстро расти, а модуль А(ω) обычно уменьшается. Поэтому АФЧХ W_τ(jω) разомкнутой системы с запаздыванием имеет вид спирали, закручивающейся вокруг начала координат (рисунок 7.4).

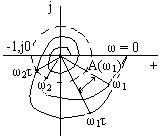
Рисунок 7.4 – Построение АФЧХ разомкнутой системы с запаздыванием

На границе устойчивости АФЧХ Wτ(jω) разомкнутой системы с запаздыванием будет проходить через точку (-1,j0). Время запаздывания τкр и соответствующее ему значение частоты ωкр , при которых Wτ(jω) проходит через точку (-1,j0) называют критическими. Для критического случая справедливо следующее условие:

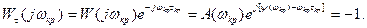(7.9)

Условие (7.9) можно записать раздельно для амплитуд и фаз:

A(ω_kp) = |Wτ(jω_kp)| = 1; (7.10)

ψ_τ(ω_kp) = ψ(ω_kp) - ω_kpτ_kp = -π(2i + 1), (7.11)

где i = 0,1,2,3 ….

Из (7.10) можно найти ω_kp , а затем из (7.11) найти τ_кр , т.е.

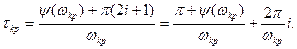(7.12)

Для систем с запаздыванием основное значение имеет Min критическое время запаздывание (при i = 0), которое является в то же время и граничным

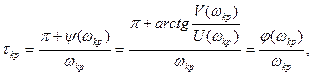(7.13)

где φ(ω_kp) = π + arctg[V(ω_kp)/U(ω_kp)] – запас устойчивости по фазе.

Пример: дана ПФ разомкнутой системы с запаздыванием

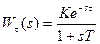
Определить критическое время запаздывания τ_kp .

Частотная ПФ разомкнутой системы с запаздыванием получается путем подстановки s = jω

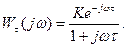
Запишем условие (7.10)

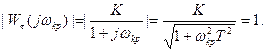
Из последнего выражения находим критическую частоту

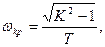К >1.

Фазовый сдвиг на критической частоте равен

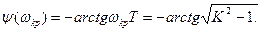
По (7.13) находим критическое время запаздывания

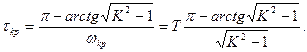
Если имеется несколько точек пересечения годографа W(jω) с окружностью единичного радиуса, то САУ будет иметь несколько критических граничных времен запаздывания. Для повышения быстродействия и точности системы время запаздывания τ стремятся уменьшить, поэтому критерий устойчивости формулируется только для минимального τ_кр из имеющихся.

Система будет устойчива, если время запаздывания меньше минимального критического времени запаздывания

τ < τ_крmin.