Рассмотрим ограниченную струну: 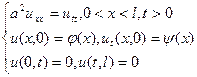 | будем решать методом разделения переменных: будем искать частные решения уравнения в виде произведения двух функций: Метод Фурье: Ищем u(x,t) в виде: 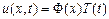 Подставляем в уравнение: Подставляем в уравнение: 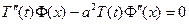 Делим на Делим на 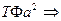 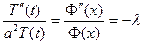 (для того чтобы тождество выполнялось, приравниваем его некоторой произвольной константе) (для того чтобы тождество выполнялось, приравниваем его некоторой произвольной константе) |
Получаем два уравнения: 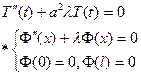 | * - это уравнение второго порядка с двумя граничными условиями, это краевая задача с тривиальным решением, но она имеет не только тривиальное решение при некоторых λ. Это задача на собственные значения. Это задача Штурмана-Лиувилля. Решим её. рассмотрим три случая: 1. λ<0 – не подходит, т.к. собственные значения должны быть не отрицательными. |
2. λ=0: 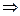 решение будет следующее: решение будет следующее: 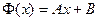 , выберем те, которые удовлетворяют краевым условиям: , выберем те, которые удовлетворяют краевым условиям: 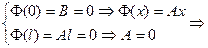 получили тривиальное решение, оно нас не интересует, поэтому этот случай тоже не подходит. 3. λ>0: получили тривиальное решение, оно нас не интересует, поэтому этот случай тоже не подходит. 3. λ>0: 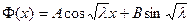 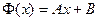 , выберем те, которые удовлетворяют краевым условиям: , выберем те, которые удовлетворяют краевым условиям: 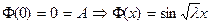 (полагаем В равным единице) (полагаем В равным единице) 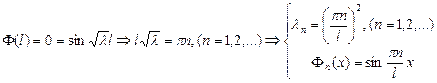 решение задачи на собственные значения. В этом решении каждому собственному значению соответствует решение задачи для Т: решение задачи на собственные значения. В этом решении каждому собственному значению соответствует решение задачи для Т: 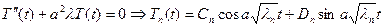 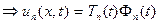 получили бесконечное множество решений задачи. Т.к. это однородные и линейные уравнения, то решения можно складывать и умножать на числа. Т.о.: получили бесконечное множество решений задачи. Т.к. это однородные и линейные уравнения, то решения можно складывать и умножать на числа. Т.о.: 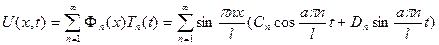 . Остались не выполненными начальные условия: . Остались не выполненными начальные условия: 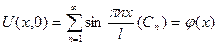 домножим обе части на домножим обе части на 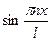 и интегрируем и интегрируем 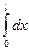 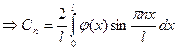 , аналогично: , аналогично: 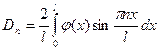 Задача решена. Проанализируем полученный результат. Введём следующие величины: Задача решена. Проанализируем полученный результат. Введём следующие величины: 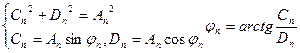 , решение тогда запишется: , решение тогда запишется: 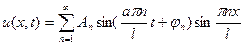 Сn – амплитуда колебаний Сn – амплитуда колебаний 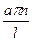 – частота колебаний, – частота колебаний, 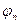 - фаза колебаний Наше решение – суперпозиция двух волн – стоячая волна, например, звук - сумма бесконечного числа стоячих волн, с соответствующей частотой, фазой и амплитудой, зависит от параметров струны: - фаза колебаний Наше решение – суперпозиция двух волн – стоячая волна, например, звук - сумма бесконечного числа стоячих волн, с соответствующей частотой, фазой и амплитудой, зависит от параметров струны: 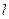 - длина струны, - длина струны, 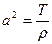 , , 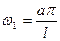 - основной тон струны, ωn – обертон, громкость зависит от C1 и D1. - основной тон струны, ωn – обертон, громкость зависит от C1 и D1. | 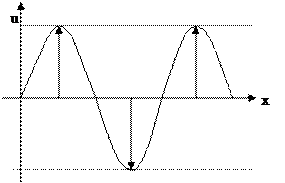 профиль колебания волны – стоячая волна. профиль колебания волны – стоячая волна. | |
| | | |
7. Смешанная краевая задача (задача Коши) 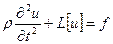 .
.
Рассмотрим линейную задачу о колебаниях среды: Разбиваем задачу на три, каждая из которых вызывает одну причину: начальное отклонение, граничные возмущения, внешние силы, т.е. 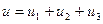 | 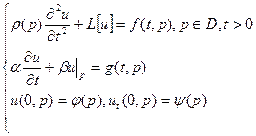 | |
1) Учитываем граничные условия: подбираем u1 таким, что бы оно удовлетворяло граничным условиям: 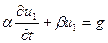 В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям. В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям. | 2) Учитываем начальные условия, не учитываем правую часть: ищем u2 такое, которое удовлетворяет однородному уравнению и однородным граничным условиям, а также получим новые начальные условия: 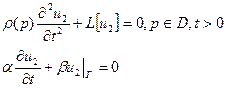 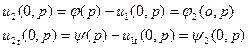 Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8. Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8. | 3) Учитываем начальные условия, не учитываем правую часть: ищем u3 такое, что бы оно удовлетворяло неоднородному уравнению, и получаем для него нулевые условия: 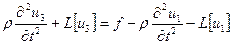 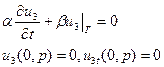 Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям. Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям. |
Рассмотрим решения задач 2 (ВОПРОС 8!) и 3 по отдельности:
3) 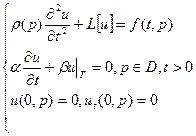 | Воспользуемся т. с. зн. 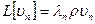 , если решение существует, то , если решение существует, то 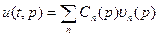 - разложили решение в ряд по собственным значениям, коэффициенты разложения ( - разложили решение в ряд по собственным значениям, коэффициенты разложения ( 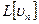 - самосопряженный оператор): - самосопряженный оператор): 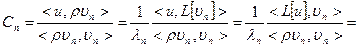 |
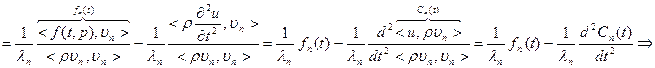 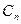 удовлетворяет уравнению: удовлетворяет уравнению: 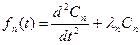 неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. 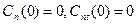 , тогда решение этого уравнения (метод вариации постоянных): , тогда решение этого уравнения (метод вариации постоянных): 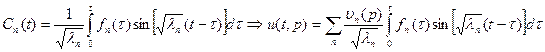 |
Наши рекомендации
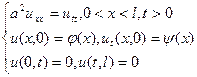
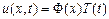 Подставляем в уравнение:
Подставляем в уравнение: 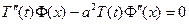 Делим на
Делим на 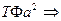
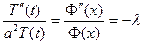 (для того чтобы тождество выполнялось, приравниваем его некоторой произвольной константе)
(для того чтобы тождество выполнялось, приравниваем его некоторой произвольной константе) 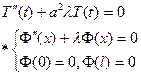
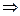 решение будет следующее:
решение будет следующее: 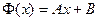 , выберем те, которые удовлетворяют краевым условиям:
, выберем те, которые удовлетворяют краевым условиям: 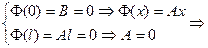 получили тривиальное решение, оно нас не интересует, поэтому этот случай тоже не подходит. 3. λ>0:
получили тривиальное решение, оно нас не интересует, поэтому этот случай тоже не подходит. 3. λ>0: 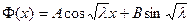
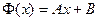 , выберем те, которые удовлетворяют краевым условиям:
, выберем те, которые удовлетворяют краевым условиям: 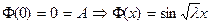 (полагаем В равным единице)
(полагаем В равным единице) 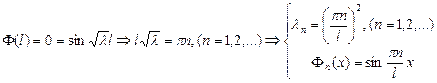 решение задачи на собственные значения. В этом решении каждому собственному значению соответствует решение задачи для Т:
решение задачи на собственные значения. В этом решении каждому собственному значению соответствует решение задачи для Т: 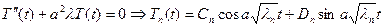
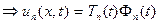 получили бесконечное множество решений задачи. Т.к. это однородные и линейные уравнения, то решения можно складывать и умножать на числа. Т.о.:
получили бесконечное множество решений задачи. Т.к. это однородные и линейные уравнения, то решения можно складывать и умножать на числа. Т.о.: 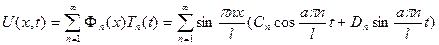 . Остались не выполненными начальные условия:
. Остались не выполненными начальные условия: 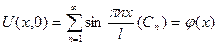 домножим обе части на
домножим обе части на 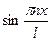 и интегрируем
и интегрируем 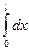
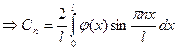 , аналогично:
, аналогично: 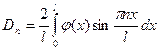 Задача решена. Проанализируем полученный результат. Введём следующие величины:
Задача решена. Проанализируем полученный результат. Введём следующие величины: 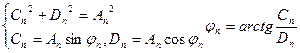 , решение тогда запишется:
, решение тогда запишется: 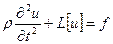 .
.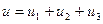
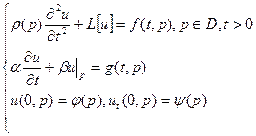
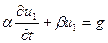 В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям.
В силу линейности оставшиеся два решения удовлетворяют однородным граничным условиям. 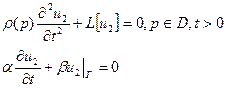
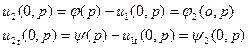 Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8.
Мы получили однородную задачу для u2 с неоднородными начальными условиями. Её решение в вопросе 8. 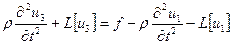
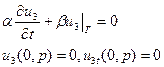 Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям.
Мы разделили задачу таким образом, что сумм этих трёх частей удовлетворяет исходным уравнению и условиям. 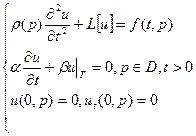
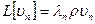 , если решение существует, то
, если решение существует, то 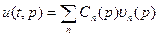 - разложили решение в ряд по собственным значениям, коэффициенты разложения (
- разложили решение в ряд по собственным значениям, коэффициенты разложения ( 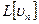 - самосопряженный оператор):
- самосопряженный оператор): 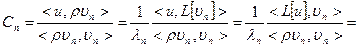
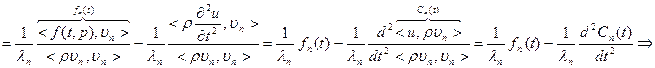
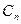 удовлетворяет уравнению:
удовлетворяет уравнению: 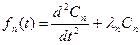 неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи.
неоднородное линейное дифференциальное уравнение второго порядка, начальные условия получаем исходя из начальных условий задачи. 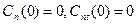 , тогда решение этого уравнения (метод вариации постоянных):
, тогда решение этого уравнения (метод вариации постоянных): 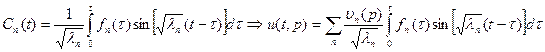

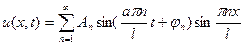 Сn – амплитуда колебаний
Сn – амплитуда колебаний 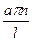 – частота колебаний,
– частота колебаний, 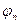 - фаза колебаний Наше решение – суперпозиция двух волн – стоячая волна, например, звук - сумма бесконечного числа стоячих волн, с соответствующей частотой, фазой и амплитудой, зависит от параметров струны:
- фаза колебаний Наше решение – суперпозиция двух волн – стоячая волна, например, звук - сумма бесконечного числа стоячих волн, с соответствующей частотой, фазой и амплитудой, зависит от параметров струны: 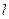 - длина струны,
- длина струны, 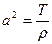 ,
, 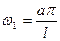 - основной тон струны, ωn – обертон, громкость зависит от C1 и D1.
- основной тон струны, ωn – обертон, громкость зависит от C1 и D1.  профиль колебания волны – стоячая волна.
профиль колебания волны – стоячая волна.