Обратная матрица. Обращение матриц второго и третьего порядка

Квадратная матрица называется обратной по отношению к матрице , если ее умножение как справа, так и слева на данную матрицу приводит к единичной матрице.

Если , то матрица называется невырожденной.

Теорема. Любая невырожденная квадратная матрица имеет единственную обратную ей матрицу.

Нахождение обратной матрицы называется обращением данной матрицы.

Для обращения матрицы можно воспользоваться формулой:

, где

Например, обратить матрицу второго порядка .

Решение.

Вычисляем определитель данной матрицы:

Находим алгебраические дополнения элементов:

Составляем союзную и обратную матрицы

,

Проверка:

Матричные уравнения и их решения.

Определение: Уравнение вида AX=B называется матричным.

Для решения матричного уравнения обе части уравнения умножаются слева на матрицу , то есть

; ;

Систему n линейных уравнений с n переменными

можно перевести в матричное уравнение AX=B, где А – матрица коэффициентов при переменных; Х – матрица – столбец переменных; В – матрица – столбец свободных членов.

Решив составленное матричное уравнение, то есть вычислив элементы матрицы Х, тем самым получаем решение данной системы.

Например, решить систему матричным методом.

Решение:

Обозначим , ,

1. следовательно матрица имеет обратную.

2.

Из алгебраических дополнений составим матрицу

3. Транспонируем матрицу :

4. Вычислим обратную матрицу по формуле:

5. Вычислим матрицу

, то есть решение системы (4; 2; 1).

Ответ: (4; 2; 1).

В конце решения системы (любым способом) рекомендуется сделать проверку, подставив найденные значения в уравнения системы, и убедится в том, что они обращаются в верные равенства.

Элементы аналитической геометрии

Координаты вектора в пространстве.

Действия над векторами в координатной форме

Пусть M(x; у; z) – координаты точки в пространстве.

Выберем: – единичные векторы на соответствующих осях координат:

Всякий вектор пространства можно представить в виде линейной комбинации единичных векторов :

,

где – координаты вектора в пространстве.

Длина вектора 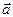вычисляется по формуле .

Рассмотрим две точки пространства: и .

Найдем координаты вектора :

Таким образом, – координаты вектора

Длина вектора определяется по формуле .

Справедливо следующее утверждение:

пусть и тогда

,

,

.

Пример 1.

Найти расстояние между точками А и В, если известно, что А(–2;3;1) и В(2;1;5).

Решение:

1. Найдем координаты вектора :

2. Вычислим длину вектора :

Ответ: 6.

Пример 2.

Найти длину вектора если .

Решение:

1. Обозначим:

2. Найдем координаты вектора

3. Найдем координаты вектора

4. Вычислим длину вектора

Ответ: 3.