Капельной жидкости в трубопроводе
Рассмотрим теперь общий случай проявления инерционных свойств потока. Предположим, что течение капельной жидкости с плотностью 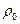 и скоростью
и скоростью 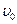 происходит в трубопроводе с площадью поперечного сечения
происходит в трубопроводе с площадью поперечного сечения 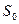 (рис. 12.3). Пусть в некотором сечении
(рис. 12.3). Пусть в некотором сечении 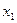 трубопровода возникает произвольное изменение
трубопровода возникает произвольное изменение 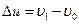 скорости этого течения, например, замедление потока или, наоборот, его ускорение. Что происходит при этом?
скорости этого течения, например, замедление потока или, наоборот, его ускорение. Что происходит при этом?
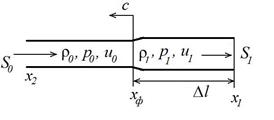
Рис. 12.3. Схема распространения волны давления
Слои жидкости, идущие сзади, тормозятся и сжимают слои жидкости, идущие впереди. При сжатии давление возрастает от значения 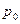 до
до 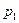 , плотность жидкости увеличивается от значения
, плотность жидкости увеличивается от значения 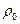 до
до 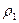 ; площадь сечения трубопровода также увеличивается от значения
; площадь сечения трубопровода также увеличивается от значения 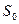 до
до 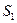 , а фронт волны
, а фронт волны 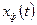 , на котором происходит сжатие, распространяется с некоторой скоростью
, на котором происходит сжатие, распространяется с некоторой скоростью 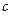 вверх по течению.
вверх по течению.
Конечно, относительные изменения 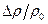 плотности жидкости и
плотности жидкости и 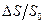 - площади сечения трубопровода малы, однако оказывается, что те и другие совершенно необходимо учитывать для адекватного описания рассматриваемого процесса.
- площади сечения трубопровода малы, однако оказывается, что те и другие совершенно необходимо учитывать для адекватного описания рассматриваемого процесса.
Вычислим относительные изменения 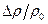 плотности жидкости и площади
плотности жидкости и площади 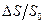 поперечного сечения трубопровода.
поперечного сечения трубопровода.
Относительное изменение 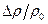 плотности упругой жидкости при изменении давления на величину
плотности упругой жидкости при изменении давления на величину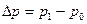 можно вычислить на основе уравнения состояния жидкости, которое, как известно, имеет вид (см. п.2 гл.2):
можно вычислить на основе уравнения состояния жидкости, которое, как известно, имеет вид (см. п.2 гл.2):
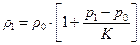 .
.
Из этого уравнения следует, что
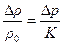 , (12.2)
, (12.2)
где 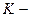 модуль упругости нефти (Па) (для нефти
модуль упругости нефти (Па) (для нефти 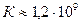 Па).
Па).
Пример. Плотность 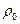 нефти при давлении 0,1 МПа равна 870 кг/м3. Какова ее плотность
нефти при давлении 0,1 МПа равна 870 кг/м3. Какова ее плотность 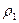 при давлении 6,5 МПа и той же самой температуре?
при давлении 6,5 МПа и той же самой температуре?
Решение. Используя формулу (12.2), получаем:
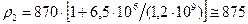 кг/м3.
кг/м3.
Отсюда видно, что увеличение 5 кг/м3 плотности нефти мало по сравнению с первоначальной плотностью 870 кг/м3.
Относительное изменение 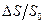 площади сечения трубопровода при изменении давления на величину
площади сечения трубопровода при изменении давления на величину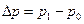 можно вычислить приближенным методом, предложенным Н.Е. Жуковским (рис. 12.4). Согласно этому методу, рассмотрим равновесие верхней половины трубы (на рис. 12.4 выделена утолщенной линией) под действием разности давлений
можно вычислить приближенным методом, предложенным Н.Е. Жуковским (рис. 12.4). Согласно этому методу, рассмотрим равновесие верхней половины трубы (на рис. 12.4 выделена утолщенной линией) под действием разности давлений 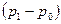 и окружных напряжений
и окружных напряжений 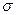 , возникающих в металле трубы.
, возникающих в металле трубы.
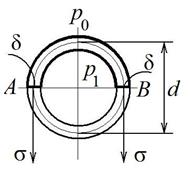
Рис. 12.4. К выводу формулы изменения площади поперечного сечения трубопровода при изменении давления
Горизонтальная равнодействующая сил давления равна, естественно, нулю, а вертикальная равнодействующая равна произведению разности 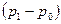 внутреннего и внешнего давлений на проекцию криволинейной стенки на горизонтальную ось.
внутреннего и внешнего давлений на проекцию криволинейной стенки на горизонтальную ось.
Таким образом, уравнение равновесия имеет вид:
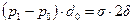 , (*)
, (*)
где 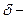 толщина стенки. Изменениями окружного напряжения
толщина стенки. Изменениями окружного напряжения 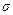 по радиусу, а также уменьшением толщины стенки пренебрегаем. Кроме того, считаем, что толщина стенки много меньше диаметра трубопровода, т.е.
по радиусу, а также уменьшением толщины стенки пренебрегаем. Кроме того, считаем, что толщина стенки много меньше диаметра трубопровода, т.е. 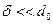 .
.
Деформация 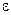 срединного волокна (на рис. 12.4 оно обозначено пунктирной линией) равна относительному удлинению этого волокна:
срединного волокна (на рис. 12.4 оно обозначено пунктирной линией) равна относительному удлинению этого волокна:
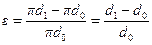 .
.
Тогда согласно закону упругости Гука, имеем:
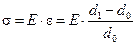 , (**)
, (**)
где 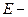 модуль Юнга материала трубы (для стали
модуль Юнга материала трубы (для стали 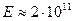 Па).
Па).
Подставив 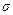 из (**) в (*) и заменив
из (**) в (*) и заменив 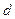 в коэффициентах на
в коэффициентах на 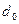 в силу малости толщины стенки по сравнению с диаметром трубы, получим формулу для приращения
в силу малости толщины стенки по сравнению с диаметром трубы, получим формулу для приращения 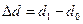 диаметра трубы в зависимости от разности
диаметра трубы в зависимости от разности 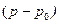 внутреннего и внешнего давлений:
внутреннего и внешнего давлений:
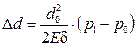 . (12.3)
. (12.3)
Из формулы (12.3) следует выражение для абсолютного 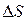 и относительного
и относительного 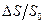 изменений площади поперечного сечения трубопровода в зависимости от изменения
изменений площади поперечного сечения трубопровода в зависимости от изменения 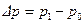 давления:
давления:
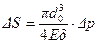 или
или 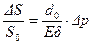 . (12.4)
. (12.4)
Замечание. При выводе этих формул методом Н.Е. Жуковского предполагалось, что при расширении трубы существуют только радиальные напряжения, а осевые - отсутствуют. В действительности это не всегда так, и в общем случае формула (12.3) имеет вид:
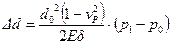 ,
, 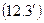
где 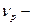 коэффициент Пуассона (второй коэффициент упругости в законе Гука). Аналогично изменяются и формулы (12.4):
коэффициент Пуассона (второй коэффициент упругости в законе Гука). Аналогично изменяются и формулы (12.4):
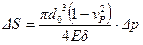 ,
, 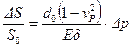 . (
. ( 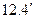 )
)
Однако коэффициент Пуассона стали мал 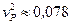 , поэтому для расчетов часто используют формулы (12.3) и (12.4):
, поэтому для расчетов часто используют формулы (12.3) и (12.4):
Пример. Рассчитать увеличение внутреннего диаметра и площади сечения стального нефтепровода ( 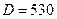 мм,
мм, 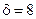 мм) после того, как в нем подняли давление на 5,0 МПа.
мм) после того, как в нем подняли давление на 5,0 МПа.
Решение. Воспользовавшись формулами (12.3) и (12.4 ), получаем:
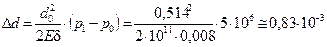 м
м 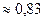 мм.
мм.
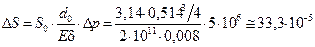 м2
м2  3,3 см2.
3,3 см2.
Как и следовало ожидать, увеличение площади поперечного сечения трубопровода на 3,3 см2 мало по сравнению с первоначальной площадью 2074 см2.
