Давление жидкости на плоскую стенку

Выведем формулу для определения силы суммарного гидростатического давления P, действующего на плоскую стенку произвольного очертания, расположенную под поверхностью жидкости под произвольным углом α к горизонту (рис. 2.8). Выделим на рассматриваемой стенке элементарную площадку .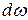

Силу давления на элементарную площадку dω, расположенную на глубине h, можно записать в виде

.

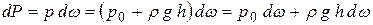Здесь p₀ – давление на поверхности жидкости.

Если l – координата в плоскости стенки, то 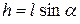. Тогда

.

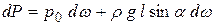(2.12)

Чтобы найти величину силы давления, действующей на всю площадь ω, нужно проинтегрировать элементарную силу dP, действующую на площадку dω, по площади ω:

.

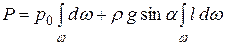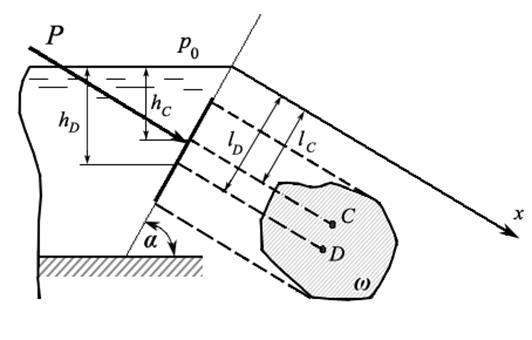
Рис. 2.8

Интеграл 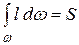является статическим моментом площади стенки ω относительно оси x, которая представляет собой линию пересечения наклонной плоскости стенки с поверхностью жидкости. Этот момент можно представить как

,

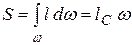где l_C – координата центра тяжести.

Тогда, учитывая, что

,

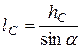где h_C – глубина погружения центра тяжести площадки, получим

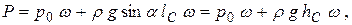(2.13)

или

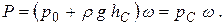
Здесь p_C – давление в центре тяжести стенки.

Таким образом, полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление p_С в центре тяжести этой площадки.

Внешнее давление p₀ передается всем точкам площадки ω одинаково, поэтому его равнодействующая будет приложена в центре тяжести площадки. А давление от веса жидкости распределится по площадке неравномерно.

Точка приложения равнодействующей сил гидростатического давления называется центром давления.

Найдем координату центра давления на площадке ω. Будем считать для простоты, что на стенку действуют только силы избыточного давления, т. е.

p₀= 0.

Обозначим центр давления буквой D. Тогда его координата по стенке будет l_D. Вспомним теорему механики о том, что момент равнодействующей силы (в нашем случае – гидростатического давления) относительно оси (возьмем ось Оx) равен сумме моментов составляющих сил, т. е.

.

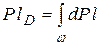Из формулы (2.12) определим величину dP и, с учетом того, что p₀= 0, получим

,

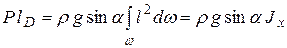где J_x – момент инерции площадки ω относительно оси x.

Отсюда:

.

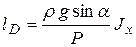Подставим в эту формулу значение P из выражения (2.13) и, учитывая, что p₀ = 0, получим:

.

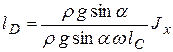Выразим момент инерции относительно оси x – J_x – через момент инерции относительно оси, проходящей через центр тяжести площадки ω и параллельной оси x – J_C :

.

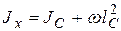Тогда окончательно имеем:

.

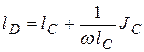(2.14)

Из этой формулы видно, что l_D всегда будет больше l_C, т. е. центр давления лежит глубже, чем центр тяжести площадки ω. Величина 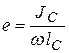имеет размер длины и называется эксцентриситетом давления. Эксцентриситет давления уменьшается с увеличением глубины погружения площадки.

Если площадь ω имеет ось симметрии, перпендикулярную оси x, то формула (2.14) полностью определяет положение центра давления. В случае несимметричной фигуры нужно отыскать вторую координату центра давления в направлении, параллельном оси x. Построим ось y, перпендикулярную оси x, и проведем все расчеты и рассуждения, аналогичные вышеприведенным, относительно этой оси. Получим:

.

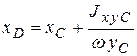Здесь 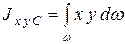– центробежный момент инерции площадки ω относительно осей x и y. Следует иметь в виду, что центробежный момент инерции может быть и положительным, и отрицательным, в зависимости от расположения оси y.

В предыдущих рассуждениях принято, что давление на поверхности жидкости p₀ равно нулю. Если оно отлично от нуля, то учесть его можно так: точкой приложения силы внешнего давления на площадку будет центр тяжести этой площадки; точкой приложения избыточного давления является центр давления. Зная две этих силы и точки их приложения, можно найти общий центр давления на площадку, при этом полная сила давления на площадь ω будет равна сумме внешнего и избыточного давлений.