Основные теоретические сведения и расчетные формулы

Рассматриваемая задача относится к разделу "Геометрические ха­рак­терис­тики плоских фигур".

При расчете на изгиб, кручение и другие виды более сложного нагру­жения для оценки прочности и жесткости бруса недостаточно знать только площадь его поперечного сечения, требуется определять другие гео­метрические характеристики сечения: статический момент пло­щади, осевые, центробежный и полярный моменты инерции.

Таблица 3 - Числовые данные к задаче № 3

Номер	Номер расчет. схемы	Размер	Прокатный профиль
строки	(Рисунок 5,6)	а, см	полоса	швеллер	двутавр	уголок
			160´10			75´75´8
			180´10			75´50´6
			180´6			90´90´6
			200´10	14а		80´50´6
			200´6			80´80´8
			160´8	16а		70´45´5
			210´8			75´75´6
			220´10			80´50´6
			220´8	14а		70´70´6
			180´8			63´40´6

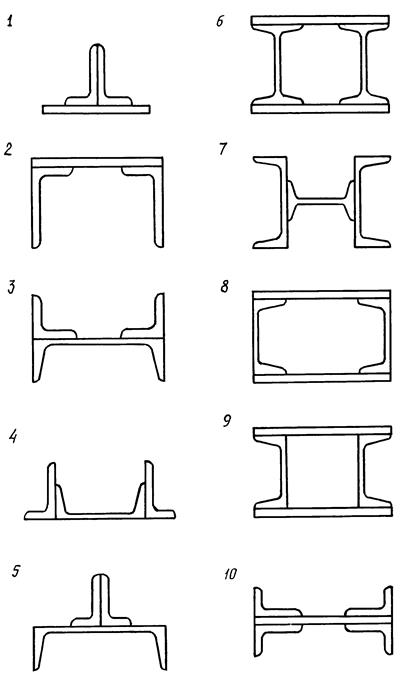
Рисунок 5 - Расчетные схемы к задаче № 3 (для первого сечения)

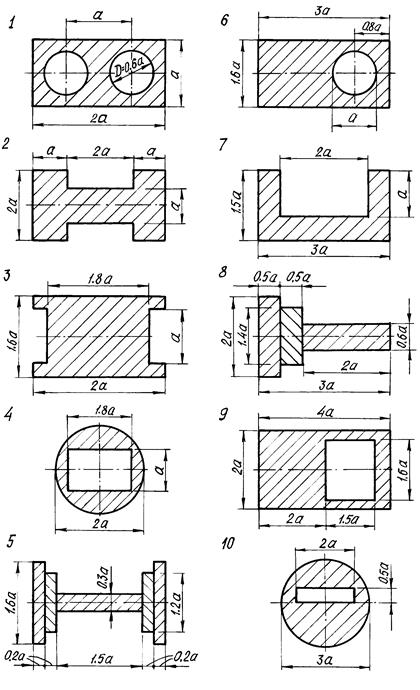
Рисунок 6 - Расчетные схемы к задаче № 3 (для второго сечения)

O

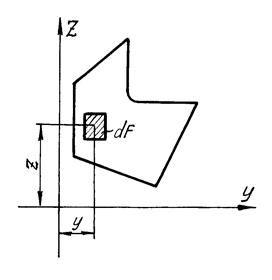Рассмотрим произвольную плоскую фигуру площадью F, отнесенную к системе координат zoy (Рисунок 7).

Обозначим: dF - площадь элементарной площадки; y, z - расстояние ее центра тяжести до осей координат.

Выражения вида

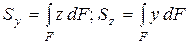(3.1)

называются статическими моментами площади относительно осей y и z соответственно.

Рисунок 7 - Плоская фигура

Зная величины статических моментов площади фигуры, можно вычислить ко­ординаты ее центра тяжести. Если за­дан­ное сечение можно разбить на части, для которых известны положения их центров

тяжес­ти и величины площадей, коорди­на­­ты центра тяжести всей фигуры определяются по формулам

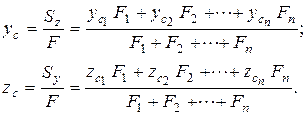(3.2)

где n - число элементов, на которое разбивается сечение;

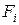- площади отдельных элементов сечения;

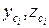- координаты центров тяжести этих элементов в выбранной системе

координат y, z.

Центр тяжести лежит на оси симметрии сечения, а если таких осей несколько - в точке их пересечения.

Моментами инерции (осевыми моментами инерции) относительно осей y и z соответственно называются интегралы вида

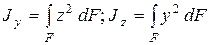(3.3)

Для простейших фигур и прокатных профилей величины моментов инер­ции приводятся в учебной и справочной литературе.

Выражение

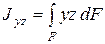(3.4)

называется центробежным моментом инерции. Оси, относительно ко­то­рых центробежный момент инерции равен нулю, называются глав­ными осями. Если хотя бы одна из выбранных координатных осей является осью сим­метрии, то обе эти оси будут главными. Осевые моменты инерции отно­сительно главных центральных осей называются главными центральными моментами инерции. Они являются экстремальными по величине: один из них макси­ма­лен, другой минимален.

Осевой момент инерции составного сечения вычисляется как сумма осе­вых моментов инерции отдельных составляющих фигур относительно одной и той же оси. При этом необходимо помнить, что в таблицах сор­тамента про­катных профилей моменты инерции простых элементов опре­делены отно­сительно их собственных центральных осей, которые пока­зываются на чер­тежах. Центральные оси составной фигуры обычно не сов­падают с таблич­­ными, и для вычисления моментов инерции подобных фи­гур приходится ис­пользовать зависимость между моментами инерции от­но­сительно парал­лельных осей:

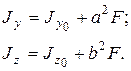(3.5)

где 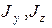- моменты инерции сечения относительно произвольных осей;

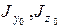- моменты инерции сечения относительно центральных осей;

F - площадь фигуры ;

а и в - расстояние между осям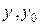и и 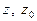соответственно.