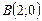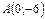Задачи для самостоятельного решения. Аналитическая геометрия на плоскости
Аналитическая геометрия на плоскости
Пример 1.Построить прямые:
а) 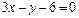 ; б)
; б) 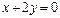 ; в)
; в) 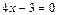 ; г)
; г) 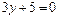 .
.
Решение.
а) Для построения прямой достаточно знать координаты двух ее произвольных точек. Полагая в уравнении 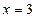 , получим
, получим 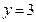 . Точка
. Точка 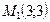 лежит на прямой. Полагая
лежит на прямой. Полагая 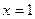 , получим
, получим 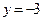 . Вторая точка
. Вторая точка 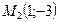 . Проводим прямую
. Проводим прямую 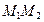 (рис. 4.1).
(рис. 4.1).
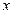
Рис. 4.1 | Задачу можно решить иначе, используя уравнение прямой в отрезках. Приведем уравнение к виду (4.5). Для этого перенесем свободный член (-6) в правую часть уравнения и обе его части разделим на 6. Получим: 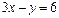 ; ; 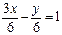 ; ; 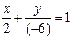 . На оси . На оси 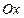 отложим 2 единицы вправо от точки отложим 2 единицы вправо от точки 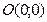 . На оси . На оси 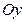 отложим 6 единиц вниз. отложим 6 единиц вниз. |
Получим точки 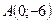 и
и 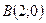 на осях, через которые проведем прямую.
на осях, через которые проведем прямую.
б) Прямая 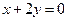 проходит через точку
проходит через точку 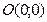 .
.
 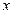 Рис. 4.2 | Полагая 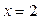 , получаем , получаем 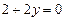 , , 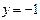 . Точка . Точка 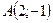 лежит на прямой. Проводим прямую через точки лежит на прямой. Проводим прямую через точки 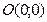 и и 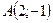 (рис. 4.2). (рис. 4.2). |
в) Разрешим уравнение относительно 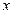 , получаем
, получаем 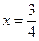 . Это прямая, параллельная оси
. Это прямая, параллельная оси 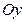 , отсекает на оси
, отсекает на оси 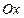 отрезок, равный
отрезок, равный 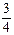 .
.
г) Запишем уравнение в виде 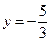 . Эта прямая параллельна оси
. Эта прямая параллельна оси 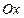 .
.
Пример 2.Уравнение прямой 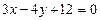 представить в различных видах (с угловым коэффициентом, в отрезках).
представить в различных видах (с угловым коэффициентом, в отрезках).
Решение. Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно 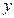 . Получим
. Получим 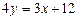 ,
, 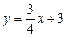 - уравнение прямой с угловым коэффициентом: здесь
- уравнение прямой с угловым коэффициентом: здесь 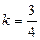 ;
; 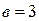 .
.
Для получения уравнения в отрезках на осях координат перенесем свободный член 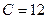 в правую часть и разделим обе части уравнения на (-12). Получим
в правую часть и разделим обе части уравнения на (-12). Получим 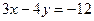 ,
, 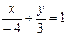 - уравнение в отрезках: здесь
- уравнение в отрезках: здесь 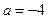 ;
; 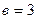 .
.
Пример 3.Составить уравнение прямой, проходящей через точку 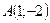
а) под углом 1350 к оси 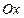 ;
;
б) параллельно оси 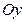 ;
;
в) перпендикулярно вектору 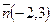 ;
;
г) и точку 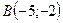 .
.
Решение.
а) Будем искать уравнение прямой с угловым коэффициентом, т.е. уравнение вида (4.6). По условию 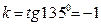 . Значит
. Значит 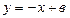 . Параметр
. Параметр 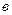 найдем из условия принадлежности точки
найдем из условия принадлежности точки 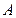 искомой прямой. Подставляя координаты точки
искомой прямой. Подставляя координаты точки 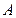 в уравнение, получим
в уравнение, получим 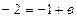 ,
, 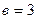 . Уравнение искомой прямой имеет вид
. Уравнение искомой прямой имеет вид 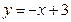 .
.
б) Уравнение прямой, проходящей через точку 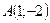 параллельно оси
параллельно оси 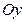 имеет вид
имеет вид 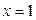 .
.
в) Чтобы записать уравнение прямой, заданной точкой 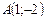 и нормальным вектором
и нормальным вектором 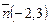 , воспользуемся уравнением (4.2):
, воспользуемся уравнением (4.2):
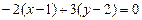 ;
;
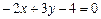 .
.
г) Используем уравнение (4.3). Полагая 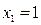 ,
, 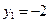 ;
; 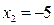 ,
, 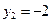 , получим
, получим 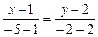 ;
;
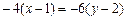 ;
;
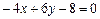 или
или 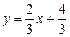 .
.
Пример 4.Найти уравнение прямой, проходящей через точку 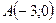 :
:
а) параллельно прямой 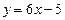 ;
;
б) перпендикулярно этой же прямой.
Решение. Будем искать уравнение прямой в виде 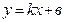 . Прямая проходит через точку
. Прямая проходит через точку 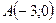 , значит
, значит 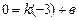 ,
, 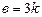 . Уравнение искомой прямой приобретает вид:
. Уравнение искомой прямой приобретает вид: 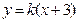 . Осталось найти
. Осталось найти 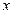 .
.
а) Если прямая параллельна прямой 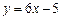 , то
, то 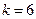 , так как угловые коэффициенты параллельных прямых равны (1.8). Значит
, так как угловые коэффициенты параллельных прямых равны (1.8). Значит 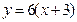 или
или 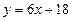 .
.
б) Если прямая перпендикулярна прямой 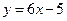 , то
, то 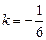 по условию (4.9). Значит
по условию (4.9). Значит 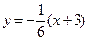 или
или 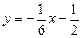 .
.
Пример 5. Найти расстояние от точки пересечения двух прямых 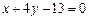 и
и 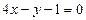 до биссектрисы первого координатного угла.
до биссектрисы первого координатного угла.
Решение. Найдем точку 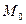 пересечения данных прямых. Для этого решим систему по формулам Крамера:
пересечения данных прямых. Для этого решим систему по формулам Крамера:
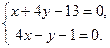
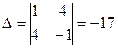 ;
; 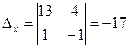 ;
; 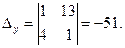
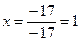 ;
; 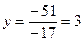 , т.е.
, т.е. 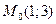 .
.
По формуле (4.11) находим расстояние 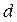 до прямой
до прямой 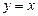 или
или 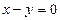 - биссектрисы первого координатного угла:
- биссектрисы первого координатного угла:
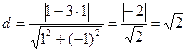 .
.
Пример 6.Даны вершины треугольника 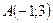 ,
, 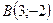 ,
, 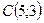 . Составить уравнения:
. Составить уравнения:
а) стороны 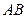 ;
;
б) медианы, проведенной из вершины 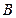 ;
;
в) высоты, опущенной из вершины 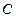 на сторону
на сторону 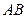 . Найти угол между медианой и высотой.
. Найти угол между медианой и высотой.
Решение.
а) Уравнение стороны 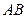 данного треугольника найдем с использованием формулы (4.3):
данного треугольника найдем с использованием формулы (4.3): 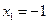 ,
, 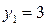 ;
; 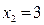 ,
, 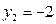 :
: 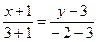 ;
; 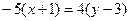 ;
;
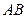 :
: 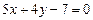 .
.
б) Чтобы составить уравнение медианы 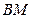 , найдем координаты точки
, найдем координаты точки 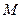 - середины отрезка
- середины отрезка 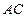 :
:
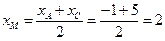 ,
, 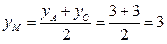 ,
,
т.е. 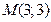 .
.
По формуле (4.3) 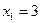 ,
, 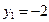 ;
; 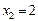 ,
, 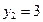 , имеем
, имеем
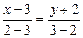 ;
; 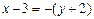 ;
;
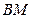 :
: 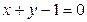 .
.
в) Высота 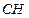 из вершины
из вершины 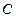 есть прямая, перпендикулярная
есть прямая, перпендикулярная 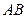 и проходящая через точку
и проходящая через точку 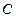 . Вектор
. Вектор 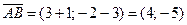 является нормальным вектором высоты. Воспользуемся уравнением (1.2):
является нормальным вектором высоты. Воспользуемся уравнением (1.2):
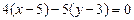 ;
; 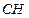 :
: 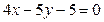 .
.
Угол между медианой 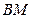 и высотой
и высотой 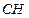 найдем по формуле (1.7). Угловой коэффициент медианы из уравнения медианы:
найдем по формуле (1.7). Угловой коэффициент медианы из уравнения медианы:
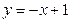 ;
; 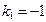 .
.
Угловой коэффициент высоты 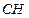 из уравнения
из уравнения 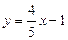 равен
равен 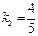 :
: 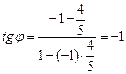 ;
; 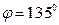 .
.
Пример 6.Построить множество решений неравенства 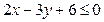 .
.
Решение. Множество решений линейного неравенства с двумя переменными 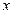 и
и 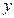 является одна из полуплоскостей, на которые делится вся плоскость прямой
является одна из полуплоскостей, на которые делится вся плоскость прямой 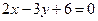 .
.

Рис. 4.3 | Полагая 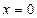 , получим , получим 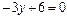 , , 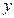 =2. Полагая =2. Полагая 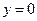 , получим , получим 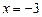 . . 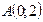 , , 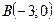 - это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3). Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой. - это точки пересечения прямой с осями координат. Построим прямую (рис. 4.3). Для определения искомой полуплоскости рекомендуется задать произвольную контрольную точку, не лежащую на ее границе – построенной прямой. |
Если неравенство выполняется в контрольной точке, то оно выполняется и во всех точках полуплоскости, содержащей контрольную точку, и не выполняется во всех точках другой полуплоскости.
И, наоборот, в случае невыполнения неравенства в контрольной точке, оно не выполняется во всех точках полуплоскости, содержащей контрольную точку, и выполняется во всех точках другой полуплоскости.
В качестве контрольной точки удобно взять начало координат 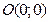 , не лежащей на построенной прямой. Координаты точки
, не лежащей на построенной прямой. Координаты точки 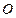 не удовлетворяют неравенству
не удовлетворяют неравенству 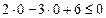 , следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку
, следовательно, решением данного неравенства является верхняя полуплоскость, не содержащая контрольную точку 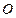 (рис. 4.3).
(рис. 4.3).
Задачи для самостоятельного решения
1.Написать уравнение прямой, проходящей через точку 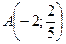 и образующей с осью
и образующей с осью 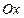 угол, равный
угол, равный 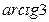 .
.
2.Какой угол образует с положительным направлением оси абсцисс прямая 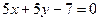 ?
?
3.Определить при каком значении 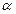 прямая
прямая 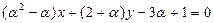
а) параллельна оси 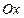 ;
;
б) проходит через начало координат?
4. Найти угловой коэффициент прямой и ординату точки ее пересечения с осью 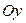 , зная, что прямая проходит через точки
, зная, что прямая проходит через точки 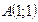 и
и 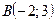 .
.
5. Прямая проходит через точки 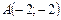 и
и 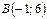 . Какую абсциссу имеет точка
. Какую абсциссу имеет точка 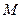 , лежащая на прямой и имеющая ординату, равную 22?
, лежащая на прямой и имеющая ординату, равную 22?
6.Найти уравнение прямой:
а) образующей с осью 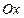 угол
угол 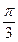 и пересекающей ось
и пересекающей ось 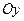 в точке (0; -6);
в точке (0; -6);
б) параллельной оси 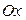 и отсекающей на оси
и отсекающей на оси 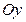 отрезок, равный 2;
отрезок, равный 2;
в) отсекающей на осях координат отрезки, равные 3 и 4.
7. Дана прямая 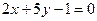 . Составить уравнение прямой, проходящей через точку
. Составить уравнение прямой, проходящей через точку 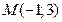 :
:
а) параллельно данной прямой;
б) перпендикулярно данной прямой.
8. Составить уравнение прямой, проходящую через точку пересечения прямых 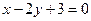 и
и 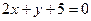 и параллельную оси ординат.
и параллельную оси ординат.
9. Составить уравнение перпендикуляра к прямой 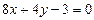 в точке пересечения ее с прямой
в точке пересечения ее с прямой 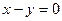 .
.
10. Найти угол между прямыми
а) 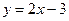 и
и 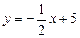 ;
;
б) 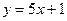 и
и 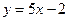 ;
;
в) 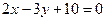 и
и 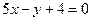 .
.
11. Найти расстояние от точки 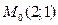 до прямой
до прямой 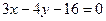 .
.
12. Показать, что прямые 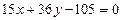 и
и 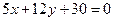 параллельны. Найти расстояние между ними.
параллельны. Найти расстояние между ними.
13. Найти длину высоты 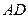 в треугольнике с вершинами
в треугольнике с вершинами 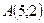 ,
, 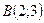 и
и 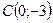 .
.
Ответы