Вычисление определителя
Решив систему уравнений методом Гаусса, можно одновременно вычислить определитель матрицы A.
Ax=f, A=LU,
где L и U - треугольные матрицы.
Определитель произведения матриц равен произведению определителей матриц. Определитель треугольной матрицы равен произведению ее диагональных элементов. Из этих двух свойств определителей следует (на главной диагонали матрицы L стоят единицы):
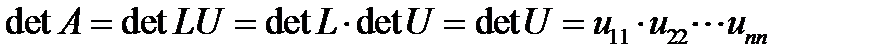 .
.
Данная формула верна при LU-факторизации без выбора главного элемента. Если был применен метод с выбором главного элемента, то для модификации формулы необходимо учитывать свойства определителя - сложение строк матрицы и умножение строки на ненулевое число не меняет определитель, но перестановка двух строк меняет знак определителя на противоположный.
Поэтому в общем случае, формула для вычисления определителя при LU-факторизации принимает вид:
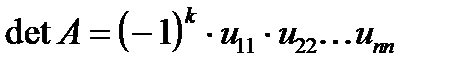 ,
,
где k - число перестановок строк или столбцов.
Примечание. При решении системы линейных алгебраических уравнений методом Гаусса нельзя заранее узнать, равен ли 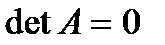 , или, другими словами, существует ли решение системы или нет.
, или, другими словами, существует ли решение системы или нет.
Если матрица A вырождена (т.е. 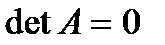 и решения не существует), то на некотором шаге исключения k-го неизвестного все элементы столбца k, находящиеся на главной диагонали и под ней, окажутся равными нулю. При этом дальнейшее исключение становится невозможным и программа должна выдать сообщение о том, что решение не существует и определитель равен нулю.
и решения не существует), то на некотором шаге исключения k-го неизвестного все элементы столбца k, находящиеся на главной диагонали и под ней, окажутся равными нулю. При этом дальнейшее исключение становится невозможным и программа должна выдать сообщение о том, что решение не существует и определитель равен нулю.
Если в программе реализован метод с выбором главного элемента, то данная проверка осуществляется проще. Необходимо проверять на равенство нулю все найденные главные элементы перед проведением очередного шага исключения. Учитывая, что вещественное число на компьютере нулю точно никогда не равняется (например, число 0.00000000000000001), то необходимо проверку производить следующим образом -
If Abs(Гл.Элемент)< 0.00001 then ...
Обращение матрицы
Нахождение матрицы, обратной матрице A, эквивалентно решению матричного уравнения 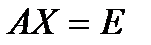 , где E - единичная матрица, X - искомая квадратная матрица.
, где E - единичная матрица, X - искомая квадратная матрица.
Для дальнейшего важно заметить, что матричная система распадается на n независимых систем уравнений с одной и той же матрицей A, но с разными правыми частями. Эти системы имеют вид:
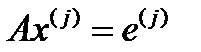 ,
, 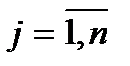 .
.
где 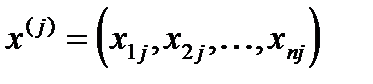 и
и 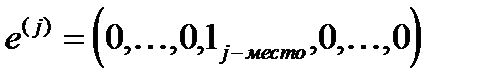 .
.
Для решения подобной задачи можно использовать различные численные методы, но наиболее эффективным методом будет метод Гаусса с LU-факторизацией. Достаточно выполнить один раз прямой ход A=LU и потом просто решать треугольные системы уравнений Ly=f и Ux=y.
Схема Халецкого
Схема Халецкого представляет собой вариант метода Гаусса с LU-факторизацией. Для системы уравнений Ax=f используют замену A=BC, где B - левая нижняя треугольная матрица, C - правая верхняя треугольная матрица с 1 по главной диагонали. Далее решают две системы уравнений с треугольными матрицами.
Элементы матриц B и C определяют по формулам:
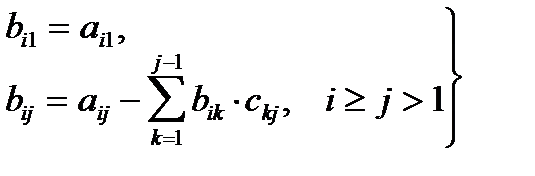 (3.7)
(3.7)
и
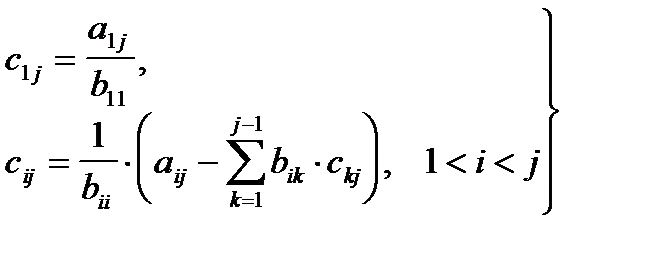 . (3.8)
. (3.8)
Далее искомый вектор x может быть вычислен из цепи уравнений:
By=f и Cx=y.
Решение y и x данных систем может быть получено по формулам:
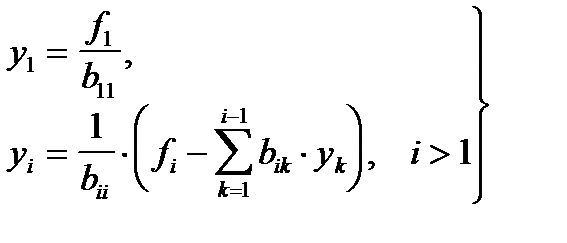 (3.9)
(3.9)
и
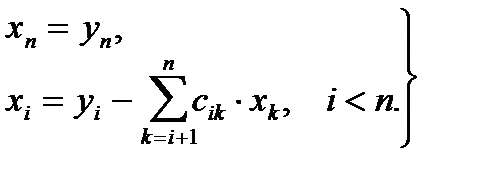 . (3.10)
. (3.10)
Числа 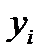 можно вычислять вместе с коэффициентами
можно вычислять вместе с коэффициентами 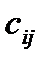 .
.
Если матрица A симметрическая, т.е. 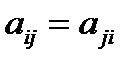 , то для определения коэффициентов
, то для определения коэффициентов 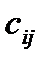 используется более простая формула
используется более простая формула
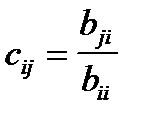 .
.
Для хранения матриц B и C можно использовать два массива, но, принимая во внимание вид матрицы C, возможно и сократить количество массивов до 1. При этом необходимо будет специально учитывать, что 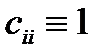 .
.
