Бесконечно малые и бесконечно большие функции
Функция, ОДЗ
Пусть заданы 2 множества Х,У функцией или отображением из Х в У называется правило, по которому каждому значению их Х ставится в соотвествие значение из У.
Числовые функции характеризуются тем, что оба множества Х и У являются подмножествами множества действительных чисел (или совпадают с ними). Область определения функции - множество возможных значений, которые может принимать аргумент.
Графиком функции с областью определения называется множетсво точек Г={(x,f(x)|xÎX}.
Свойства функции.
1. Чётность. Если облать определения функции симметричня относительно нуля и f(-x)=f(x) "xÎD(f), то функция у=f(x) называется чётной. Если
f(-x)= - f(x) "xÎD(f), то функция у=f(x) называется нечётной. Если не выполняется ни первое, ни второе условие, то функция обшего вида.
2. Монотонность. функция у=f(x) – возрастающая , если для любого х1 и х2 из области определения функции (х1<х2) выполняется неравенство f(x1)<f(x2)
Функция у=f(x) – убывающая, если для любого х1 и х2 из области определения функции (х1>х2) выполняется неравенство f(x1)>f(x2).
Возрастающие или убывающие функции называются монотонными.
3. Ограниченность. Функция у=f(x) называется ограниченной на некотором промежутке , если существует М>0, MÎR|"xÎданному промежутку |f(x)|£M.
Функция у=f(x) называется ограниченной снизу, если существует mÎR |"xÎданному промежутку m£f(x). Функция у=f(x) называется ограниченной сверху, если существует mÎR |"xÎданному промежутку m³f(x).
4. Периодичность. Функция у=f(x) называется периодической с периодом Т не равным нулю, если выволняется условие f(x+ - T)=f(x).
Обратная функция.
Пусть Функция у=f(x) задана на множестве Х=D(f) и Y=E(f). Предположим, что различным значениям х1 и х2 соответствуют различные значения функции f(x1) и f(x2). Тогда для любого уÎУ мы сможем поставить в соответсвие хÎХ| y=f(x). Получает отображение f-1: У®Х. Это отображение называется обратным. График прямой и обратной функции симметричен относительно биссектрисы первой и третьей координатной четверти.
Сложная функция.
Пусть заданы две функции t=h(x), [xÎD(h), T=E(h)] и y=g(t), [tÎT=D(g), Y=E(g)] (область определения одной функции совпадает с областью значений другой функции и наоборот) Тогда справедливо следующее правило: из любого хÎХ по правилу ставится в соответствие y=g(h(x)). Это правило называется сложной функцией.
Основные элементарные функции.
1. Степенная. y=xa, a=const, aÎR. D(f)=(0;+¥). Если aÎNÞD(f)=R.
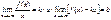 2. Показательная. y=ax, a>0,a не равно 1. D(f)=R/ E(f)=(0;+¥). Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает.
2. Показательная. y=ax, a>0,a не равно 1. D(f)=R/ E(f)=(0;+¥). Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает.
3. Логарифмическая. y=logax, a>0, a не равно 1. D(f)=(0;+¥), E(f)=R. Если a>1, следовательно, функция возрастает. Если аÎ(0;1), функция убывает.
4. Тригонометрические.
5. Обратные тригонометрические.
Предел функции
Опр. Пределом функции у=f(x) в точке х0 (или при х →х0 )называют число а, если для любой последовательности { хn} значений аргумента , сходящейся к (при этом все хn≠ х0) последовательность значений функции сходится к пределу а. Это записывают в виде:
(*)
Аналогично определяеся предел при х →∞ (случаи когда х0 есть +∞ или -∞). А именно, равенство (*) во всех случаях означает следующее: для любой последовательности { хn}, сходящейся к х0 , соответствующая последовательность {f(хn)} сходится к а.
Бесконечно малые и бесконечно большие функции.
Опр. Функция f(x) наз.бесконечно малой при х →х0, если

и бесконечно большой при х →х0 , если
Справедливы теоремы. 1.Сумма и произведение двух бесконечно малых функций (при х →х0) снова являются бесконечно малыми функциями (при х →х0).
