Свойства линий второго порядка

157. Эллипс касается оси абсцисс в точке А(3; 0) и оси ординат в точке В(0; –4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

158. Установить, что уравнение 5x² + 9y² – 30x + 18y + 9 = 0 определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис.

159. Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке F(–1; 0), чем к прямой x = –4.

160. Установить, какую линию определяет уравнение 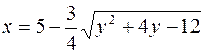. Изобразить эту линию на чертеже.

161. Составить уравнение параболы, если дан фокус F(–7; 0) и уравнение директрисы x – 7 = 0.

162. Установить какую линию определяет уравнение 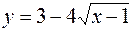. Изобразить эту линию на чертеже.

163. Составить уравнение параболы, если даны ее фокус F(7; 2) и директриса x – 5 = 0.

164. Определить точки пересечения эллипса 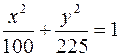и параболы y² = 24x.

165. Точка С(–3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

166. Установить, какую линию определяет уравнение 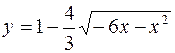. Изобразить эту линию на чертеже.

167. Определить траекторию точки М, которая при своем движении остается втрое ближе к точке А(1; 0), чем к прямой x = 9.

168. Установить, что уравнение 9x² – 16y² + 90x + 32y – 367 = 0 определяет гиперболу, и найти координаты его центра С, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис.

169. Написать уравнение параболы и ее директрисы, если парабола проходит через точки пересечения прямой x + y = 0 и окружности x² + y² + 4y = 0 и симметрична относительно оси Oy. Построить окружность, прямую и параболу.

170. Составить уравнение параболы, если даны ее фокус F(4; 3) и директриса y + 1 = 0.

171. Определить точки пересечения гиперболы 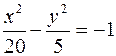и параболы y² = 3x.

Ранг матрицы

Найти ранг матриц:

172. 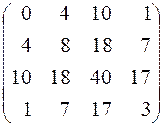. 173. .

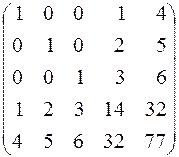174. .

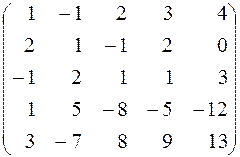175. Найти размерность и базис подпространства пространства строк, натянутого на данную систему векторов: f₁ = (2; 0; 1; 3; –1), f₂ = (1; 1; 0; –1; 1), f₃ = (0; –2; 1; 5; –3), f₄ = (1; –3; 2; 9; –5).

Найти ранг матриц:

176. 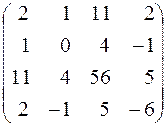. 177. .

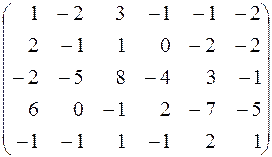178. .

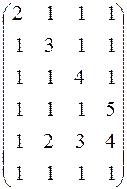Найти размерность и базис подпространства пространства строк, натянутого на данную систему векторов:

179. f₁ = (2; 1; 3; 1), f₂ = (1; 2; 0; 1), f₃ = (–1; 1; –3; 0);

180. f₁ = (2; 1; 3; –1), f₂ = (–1; 1; –3; 1), f₃ = (4; 5; 3; –1), f₄ = (1; 5; –3; 1).

Действия с матрицами

Выполнить действия: 181. .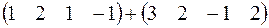

182. .

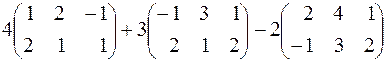Умножить матрицы: 183. .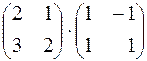

184. 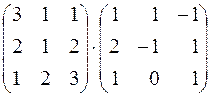. 185. 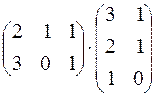. 186. .

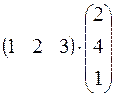Обратить матрицы:

187. 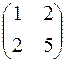. 188. 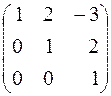. 189. .

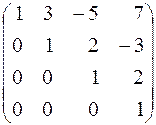Выполнить действия:

190. .

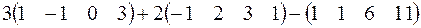Умножить матрицы: 191. 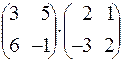. 192. .

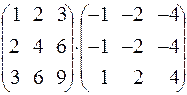193. 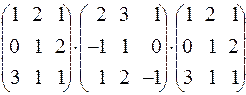. 194. 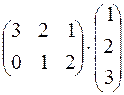. 195. .

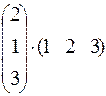196. Вычислить АА^Т, где А = 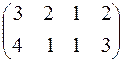, если А^Т – матрица, транспонированная к А.

Обратить матрицы: 197. 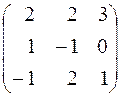. 198. .

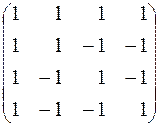Решение уравнений матричным способом

Решить матричные уравнения: 199. .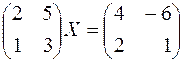

200. .

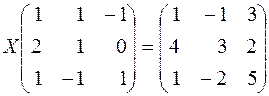201. .

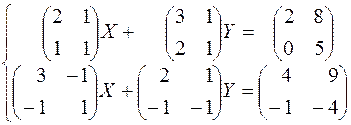Решить системы уравнений: 202.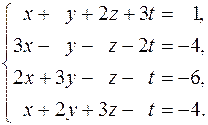

203. 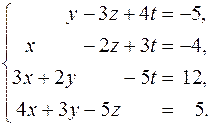204.

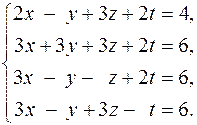
Решить матричные уравнения:

205. 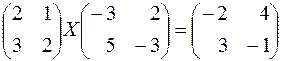. 206.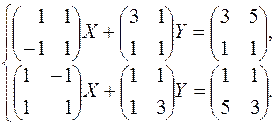

Решить системы уравнений:

207. 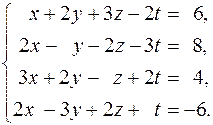208.

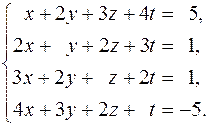
Базис в пространстве

В пространстве строк над числовым полем дана система векторов f₁, f₂, …, f_m. Выделить максимальную линейно независимую подсистему и выразить остальные векторы в виде линейных комбинаций векторов выделенной подсистемы:

209. 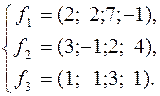210.

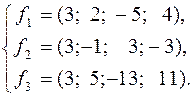
211. 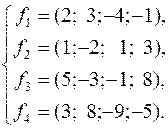212.

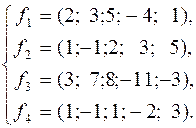
213. Можно ли принять {f₁, f₂, f₃, f₄}, где f₁ = (1; 1; 0; 1), f₂ = (2; 1; 3; 1), f₃ = (1; 1; 0; 0), f₄ = (0; 1; –1; –1), за базис? Каковы координаты вектора X = (0; 0; 0; 1) в этом базисе?

Найти собственные значения и собственные векторы матриц, рассматриваемых как операторы умножения слева в пространстве столбцов над полем С:

214. 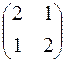. 215. 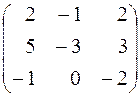. 216. .

В пространстве строк над числовым полем дана система векторов f₁, f₂, …, f_m. Выделить максимальную линейно независимую подсистему и выразить остальные векторы в виде линейных комбинаций векторов выделенной подсистемы:

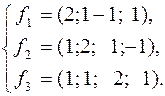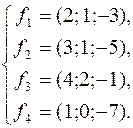217. 218. 219.

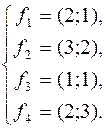
220.

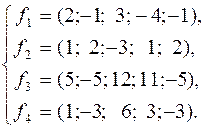
221. Можно ли принять {f₁, f₂, f₃, f₄}, где f₁ = (1; 1; 1; 1), f₂ = (1; 1; –1; –1), f₃ = (1; –1; 1; –1), f₄ = (1; –1; –1; 1), за базис? Каковы координаты вектора X = (1; 2; 1; 1) в этом базисе?

Найти собственные значения и собственные векторы матриц, рассматриваемых как операторы умножения слева в пространстве столбцов над полем С:

222. 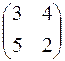. 223. .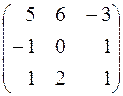