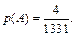Теоремы сложения и умножения вероятностей

Определение 2. Сумма двух событий А и В – это такое событие А+В, которое состоит в том, что произошло хотя бы одно из этих событий.

Определение 3. Произведение событий А и В – это такое событие А·В, состоящее в том, что эти события произошли совместно: и А и В.

Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

р(А + В) = р(А) + р(В).

Следствие 1. Вероятность суммы попарно несовместных событий А₁, А₂,…, А_n равна сумме вероятностей этих событий:

p(А₁ + А₂ +…+ А_n) = p(А₁) + p(А₂)+…+ p(А_n).

Следствие 2. Сумма вероятностей событий, образующих полную группу (то есть, когда эти события попарно несовместны, но в результате испытания одно из них произойдет обязательно), равна 1.

Следствие 3. Сумма вероятностей противоположных событий равна 1: р(А) + р( 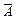) = 1, где 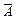– событие противоположное событию А.

Таблица 3.

Значения функции для 0 ≤ x< 1, e ≈ 2,7183

x	с о т ы е д о л и x
0,0	1,0000	0,9900	0,9802	0,9704	0,9608	0,9512	0,9418	0,9324	0,9231	0,9139
0,1	0,9048	0,8958	0,8869	0,8781	0,8694	0,8607	0,8521	0,8437	0,8353	0,8270
0,2	0,8187	0,8106	0,8025	0,7945	0,7866	0,7788	0,7711	0,7634	0,7558	0,7483
0,3	0,7408	0,7334	0,7261	0,7189	0,7118	0,7047	0,6977	0,6907	0,6839	0,6771
0,4	0,6703	0,6637	0,6570	0,6505	0,6440	0,6376	0,6313	0,6250	0,6188	0,6126
0,5	0,6065	0,6005	0,5945	0,5886	0,5827	0,5769	0,5712	0,5655	0,5599	0,5543
0,6	0,5488	0,5434	0,5379	0,5326	0,5273	0,5220	0,5169	0,5117	0,5066	0,5016
0,7	0,4966	0,4916	0,4868	0,4819	0,4771	0,4724	0,4677	0,4630	0,4584	0,4538
0,8	0,4493	0,4449	0,4404	0,4360	0,4317	0,4274	0,4232	0,4190	0,4148	0,4107
0,9	0,4066	0,4025	0,3985	0,3946	0,3906	0,3867	0,3829	0,3791	0,3753	0,3716

Примечание

1. Значения функции e ^{– x}, содержащей только тысячные доли в показателе, приведены в таблице

е–0,001 = 0,9990	е–0,004 = 0,9960	е–0,007 = 0,9930
е–0,002 = 0,9980	е–0,005 = 0,9950	е–0,008 = 0,9920
е–0,003 = 0,9970	е–0,006 = 0,9940	е–0,009 = 0,9910

2. При расчете значений функций с показателем степени, содержащим десятые, сотые и тысячные доли, можно использовать обе вышеприведенные таблицы. Например,

e ^{– 0,825}= e ^{– 0,82}∙ e ^{– 0,005}≈ 0,4404 ∙ 0,9950 ≈ 0,4382.

3. При расчете значений функции e ^{– x} при x ≥ 1 можно использовать алгебраические преобразования. Например,

e ^{– 1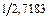}≈ ≈ 0,3679;

e ^{– 1,5}= e ^{– 1}∙ e ^{– 0,5}≈ 0,3679 ∙ 0,6065 ≈ 0,2231 или e ^{– 1,5}= e ^{– 0,75}∙ e ^{– 0,75}≈ (0,4724)² ≈ 0,2231;

e ^{– 3,5} = e ^–3∙ e ^{– 0,5}≈ (0,3679)³∙ 0,6065 ≈ 0,0302.

4. Для получения значения функции с любой требуемой точностью можно использовать формулу разложения этой функции в ряд Маклорена, сходящийся для всех x:

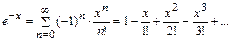(при этом погрешность получаемого значения функции определяется абсолютной величиной первого отброшенного члена ряда).

5. При расчете значений функции с положительным показателем можно воспользоваться соотношением e ^а ≈ 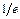^{– а}. Например, e ^0,825 = 1/ e ^{– 0,825} ≈ 1/0,4382 ≈ 2,282.

Таблица 2.

Значения нормированной функции лапласа F (x)=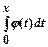

x	с о т ы е д о л и x
0,0	0,0000	0,0040	0,0080	0,0120	0,0160	0,0199	0,0239	0,0279	0,0319	0,0359
0,1	0,0398	0,0438	0,0478	0,0517	0,0557	0,0596	0,0636	0,0675	0,0714	0,0753
0,2	0,0793	0,0832	0,0871	0,0910	0,0948	0,0987	0,1026	0,1064	0,1103	0,1141
0,3	0,1179	0,1217	0,1255	0,1293	0,1331	0,1368	0,1406	0,1443	0,1480	0,1517
0,4	0,1554	0,1591	0,1628	0,1664	0,1700	0,1736	0,1772	0,1808	0,1844	0,1879
0,5	0,1915	0,1950	0,1985	0,2019	0,2054	0,2088	0,2123	0,2157	0,2190	0,2224
0,6	0,2257	0,2291	0,2324	0,2357	0,2389	0,2422	0,2454	0,2486	0,2517	0,2549
0,7	0,2580	0,2611	0,2642	0,2673	0,2704	0,2734	0,2764	0,2794	0,2823	0,2852
0,8	0,2881	0,2910	0,2939	0,2967	0,2995	0,3023	0,3051	0,3078	0,3106	0,3133
0,9	0,3159	0,3186	0,3212	0,3238	0,3264	0,3289	0,3315	0,3340	0,3365	0,3389
1,0	0,3413	0,3438	0,3461	0,3485	0,3508	0,3531	0,3554	0,3577	0,3599	0,3621
1,1	0,3643	0,3665	0,3686	0,3708	0,3729	0,3749	0,3770	0,3790	0,3810	0,3830
1,2	0,3849	0,3869	0,3888	0,3907	0,3925	0,3944	0,3962	0,3980	0,3997	0,4015
1,3	0,4032	0,4049	0,4066	0,4082	0,4099	0,4115	0,4131	0,4147	0,4162	0,4177
1,4	0,4192	0,4207	0,4222	0,4236	0,4251	0,4265	0,4279	0,4292	0,4306	0,4319
1,5	0,4332	0,4345	0,4357	0,4370	0,4382	0,4394	0,4406	0,4418	0,4429	0,4441
1,6	0,4452	0,4463	0,4474	0,4484	0,4495	0,4505	0,4515	0,4525	0,4535	0,4545
1,7	0,4554	0,4564	0,4573	0,4582	0,4591	0,4599	0,4608	0,4616	0,4625	0,4633
1,8	0,4641	0,4649	0,4656	0,4664	0,4671	0,4678	0,4686	0,4693	0,4699	0,4706
1,9	0,4713	0,4719	0,4726	0,4732	0,4738	0,4744	0,4750	0,4756	0,4761	0,4767
2,0	0,4772	0,9778	0,4783	0,9788	0,4793	0,4798	0,4803	0,4808	0,4812	0,9817
2,1	0,4821	0,4826	0,4830	0,4834	0,4838	0,4842	0,4846	0,4850	0,4854	0,4857
2,2	0,4861	0,4864	0,4868	0,4871	0,4875	0,4878	0,4881	0,4884	0,4887	0,4890
2,3	0,4893	0,4896	0,4898	0,4901	0,4904	0,4906	0,4909	0,4911	0,4913	0,4916
2,4	0,4918	0,4920	0,4922	0,4925	0,4927	0,4929	0,4931	0,4932	0,4934	0,4936
2,5	0,4938	0,4940	0,4941	0,4943	0,4945	0,4946	0,4948	0,4949	0,4951	0,4952
2,6	0,4953	0,4955	0,4956	0,4957	0,4959	0,4960	0,4961	0,4962	0,4963	0,4964
2,7	0,4965	0,4966	0,4967	0,4968	0,4969	0,4970	0,4971	0,4972	0,4973	0,4974
2,8	0,4974	0,4975	0,4976	0,4977	0,4977	0,4978	0,4979	0,4979	0,4980	0,4981
2,9	0,4981	0,4982	0,4982	0,4983	0,4984	0,4984	0,4985	0,4985	0,4986	0,4986
3,0	0,4987	0,4987	0,4987	0,4988	0,4988	0,4989	0,4989	0,4989	0,4990	0,4990
3,1	0,4990	0,4991	0,4991	0,4991	0,4992	0,4992	0,4992	0,4992	0,4993	0,4993
3,2	0,4993	0,4993	0,4994	0,4994	0,4994	0,4994	0,4994	0,4995	0,4995	0,4995
3,3	0,4995	0,4995	0,4995	0,4996	0,4996	0,4996	0,4996	0,4996	0,4996	0,4997
3,4	0,4997	0,4997	0,4997	0,4997	0,4997	0,4997	0,4997	0,4997	0,4997	0,4998
3,5	0,4998	0,4998	0,4998	0,4998	0,4998	0,4998	0,4998	0,4998	0,4998	0,4998
3,6	0,4998	0,4998	0,4998	0,4998	0,4998	0,4999	0,4999	0,4999	0,4999	0,4999
3,7	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999
3,8	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999	0,4999
Для x ≥ 3,9значение функции с точностью до четырех знаков после запятой равно 0,5000

Теорема 2. Вероятность произведения двух совместных независимых событий равна произведению вероятностей этих событий:

р(А·В) = р(А)·р(В).

Теорема 3.Вероятность произведения двух совместных зависимых событий равна произведению вероятностей одного из них на условную вероятность второго:

р(А·В) = р(А)·р(В/А) = р(В)·р(А/В),

где условная вероятность р(В/А) – вероятность события В при условии, что А произошло; условная вероятность р(А/В) – вероятность события А при условии, что В произошло.

Следствие 1. Если события А₁, А₂,…, А_n совместны и зависимы, то

p(А₁·А₂ …·А_n) = p(А₁)·p(А₂/A₁) p(А₃/A₁A₂) …·p(А_n /A₁A₂…А_n–1).

Следствие 2. Если события А₁, А₂,…, А_n независимы в совокупности, то

p(А₁·А₂ …·А_n) = p(А₁)·p(А₂) p(А₃) …·p(А_n).

Теорема 4. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

р(А+В) = р(А)+р(В) – р(А·В).

Следствие 1. Если события А и В совместны и независимы, то

р(А + В) = р(А) + р(В) – р(А)·р(В).

Следствие 2. Если события А и В совместны и зависимы, то

р(А + В) = р(А) + р(В) – р(А)·р(В/А) = р(А) + р(В) – р(В)·р(А/В).

Задача 2. Студент разыскивает нужную ему формулу в трех справочниках. Вероятность того, что формула содержится в первом, втором, третьем справочниках равна, соответственно, 0,6; 0,7; 0,8. Найти вероятность того, что формула содержится:

а) только в одном справочнике;

б) хотя бы в двух справочниках;

в) во всех трех справочниках;

г) хотя бы в одном справочнике.

Решение. Введем обозначения событий: B_i = {нужная студенту формула находится в i-м справочнике}, i = 1, 2, 3.

По условию задачи 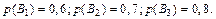Так как В_i – независимые события, то и противоположные им события 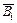– независимы: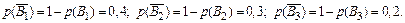

а) Событие А ={формула содержится только в одном справочнике} эквивалентно событию {формула содержится только в первом справочнике и не содержится во 2-м и 3-м; или формула содержится только во втором справочнике, но не содержится в 1-м и 3-м; или формула содержится только в третьем справочнике, но не содержится в 1-м и 2-м}. Согласно

определениям сложения и умножения событий алгеброй события A является:

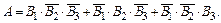
События – слагаемые в правой части последнего равенства несовместны, а события-сомножители – независимы.

По теоремам сложения и умножения вероятностей имеем:

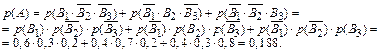
б) Событие В ={формула содержится хотя бы в двух справочниках} эквивалентно событию {формула содержится только в 1-м и во 2-м; или в 1-м и 3-м; или во 2-м и в 3-м; или в 1-м, 2-м, 3-м справочниках}, то есть

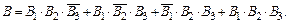
Аналогично, по теоремам сложения и умножения вероятностей:

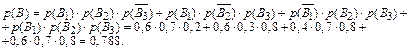
в) Событие С ={формула содержится во всех трех справочниках} эквивалентно событию {формула содержится и в 1-м, и во 2-м, и в 3-м справочниках}; то есть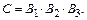

По теореме умножения независимых событий

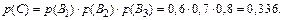
г) Событию D ={формула содержится хотя бы в одном справочнике} противоположно событие 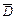= {формулы нет ни в одном справочнике}, то есть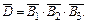

Тогда по теореме умножения независимых событий

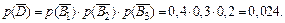
Следовательно,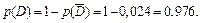

Примечание. 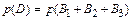, но расчеты в этом случае более затруднительны.

Ответ: а) p(A) = 0,188; p(B) = 0,788; p(C) = 0,336; p(D) = 0,976.

Задача 3. Из 11 карточек, на каждой из которых написано по одной букве: В, Е, Р, О, Я, Т, Н, О, С, Т, Ь, выбирают наугад 3 карточки, одну за другой. Найти вероятность того, что получится слово «ТОН». Рассмотреть два случая: а) выбранные карточки не возвращаются; б) каждая выбранная

Приложения

Таблица 1.

Значения функции стандартного распределения j(x)=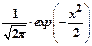

x	с о т ы е д о л и x
0,0	0,3989	0,3989	0,3989	0,3988	0,3986	0,3984	0,3982	0,3980	0,3977	0,3973
0,1	0,3970	0,3965	0,3961	0,3956	0,3951	0,3945	0,3939	0,3932	0,3925	0,3918
0,2	0,3910	0,3902	0,3894	0,3885	0,3876	0,3867	0,3857	0,3847	0,3836	0,3825
0,3	0,3814	0,3802	0,3790	0,3778	0,3765	0,3752	0,3739	0,3726	0,3712	0,3697
0,4	0,3683	0,3668	0,3653	0,3637	0,3621	0,3605	0,3589	0,3572	0,3555	0,3538
0,5	0,3521	0,3508	0,3485	0,3467	0,3448	0,3429	0,3410	0,3391	0,3372	0,3352
0,6	0,3332	0,3312	0,3292	0,3271	0,3251	0,3230	0,3209	0,3187	0,3166	0,3144
0,7	0,3123	0,3101	0,3079	0,3056	0,3034	0,3011	0,2989	0,2966	0,2943	0,2920
0,8	0,2897	0,2874	0,2850	0,2827	0,2803	0,2780	0,2756	0,2732	0,2709	0,2685
0,9	0,2661	0,2637	0,2613	0,2589	0,2565	0,2541	0,2516	0,2492	0,2468	0,2444
1,0	0,2420	0,2396	0,2371	0,2347	0,2323	0,2299	0,2275	0,2251	0,2227	0,2203
1,1	0,2179	0,2155	0,2131	0,2107	0,2083	0,2059	0,2036	0,2012	0,1989	0,1965
1,2	0,1942	0,1919	0,1895	0,1872	0,1849	0,1826	0,1804	0,1781	0,1758	0,1736
1,3	0,1714	0,1691	0,1669	0,1647	0,1626	0,1604	0,1582	0,1561	0,1539	0,1518
1,4	0,1497	0,1476	0,1456	0,1435	0,1415	0,1394	0,1374	0,1354	0,1334	0,1315
1,5	0,1295	0,1276	0,1257	0,1238	0,1219	0,1200	0,1182	0,1163	0,1145	0,1127
1,6	0,1109	0,1092	0,1074	0,1057	0,1040	0,1023	0,1006	0,0989	0,0973	0,0957
1,7	0,0940	0,0925	0,0909	0,0893	0,0878	0,0863	0,0848	0,0833	0,0818	0,0804
1,8	0,0790	0,0775	0,0761	0,0748	0,0734	0,0721	0,0707	0,0694	0,0681	0,0669
1,9	0,0656	0,0644	0,0632	0,0620	0,0608	0,0596	0,0584	0,0573	0,0562	0,0551
2,0	0,0540	0,0529	0,0519	0,0508	0,0498	0,0488	0,0478	0,0468	0,0459	0,0449
2,1	0,0440	0,0431	0,0422	0,0413	0,0404	0,0396	0,0387	0,0379	0,0371	0,0363
2,2	0,0355	0,0347	0,0339	0,0332	0,0325	0,0317	0,0310	0,0303	0,0297	0,0290
2,3	0,0283	0,0277	0,0270	0,0264	0,0258	0,0252	0,0246	0,0241	0,0235	0,0229
2,4	0,0224	0,0219	0,0213	0,0208	0,0203	0,0198	0,0194	0,0189	0,0184	0,0180
2,5	0,0175	0,0171	0,0167	0,0163	0,0158	0,0154	0,0151	0,0147	0,0143	0,0139
2,6	0,0136	0,0132	0,0129	0,0126	0,0122	0,0119	0,0116	0,0113	0,0110	0,0107
2,7	0,0104	0,0101	0,0099	0,0096	0,0093	0,0091	0,0088	0,0086	0,0084	0,0081
2,8	0,0079	0,0077	0,0075	0,0073	0,0071	0,0069	0,0067	0,0065	0,0063	0,0061
2,9	0,0060	0,0058	0,0056	0,0055	0,0053	0,0051	0,0050	0,0048	0,0047	0,0046
3,0	0,0044	0,0043	0,0042	0,0040	0,0039	0,0038	0,0037	0,0036	0,0035	0,0034
3,1	0,0033	0,0032	0,0031	0,0030	0,0029	0,0028	0,0027	0,0026	0,0025	0,0025
3,2	0,0024	0,0023	0,0022	0,0022	0,0021	0,0020	0,0020	0,0019	0,0018	0,0018
3,3	0,0017	0,0017	0,0016	0,0016	0,0015	0,0015	0,0014	0,0014	0,0013	0,0013
3,4	0,0012	0,0012	0,0012	0,0011	0,0011	0,0010	0,0010	0,0010	0,0009	0,0009
3,5	0,0009	0,0008	0,0008	0,0008	0,0008	0,0007	0,0007	0,0007	0,0007	0,0006
3,6	0,0006	0,0006	0,0006	0,0005	0,0005	0,0005	0,0005	0,0005	0,0005	0,0004
3,7	0,0004	0,0004	0,0004	0,0004	0,0004	0,0004	0,0003	0,0003	0,0003	0,0003
3,8	0,0003	0,0003	0,0003	0,0003	0,0003	0,0002	0,0002	0,0002	0,0002	0,0002
3,9	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0001	0,0001
Для 4,00 ≤ x ≤ 4,23значение функции с точностью до четырех знаков после запятой равно 0,0001
Для x ≥ 4,24значение функции с точностью до четырех знаков после запятой равно 0,0000

9.10.

X \Y								nx
	-		-	-	-	-	-
				-	-	-	-
	-						-
	-	-				-
	-	-	-	-
ny								n=100

Задача 10. Проверка гипотез.

Из генеральных совокупностей X и Y, распределенных нормально, извлечены зависимые выборки одинакового объема, варианты которых равны x_i и y_i. При уровне значимости 0,05 определить, значимо или незначимо различаются результаты. Использовать в качестве критической точки t_{двуст.кр.}(a = 0,05, k = n – 1 = 4) = 2,78.

№№ заданий по вариантам	i
10.1	xi yi
10.2	xi yi
10.3	xi yi
10.4	xi yi
10.5	xi yi
10.6	xi yi
10.7	xi yi
10.8	xi yi
10.9	xi yi
10.10	xi yi

карточка возвращается в общую совокупность, в которой все карточки перемешиваются перед извлечением следующей.

Решение. Введем следующие события:

А = {при извлечении трех карточек получится слово «ТОН»};

А₁ = {первая извлеченная буква – «Т»};

А₂ = {вторая извлеченная буква – «О»};

А₃ = {третья извлеченная буква – «Н»};

тогда событие А = А₁ ∙А₂ ∙А₃.

а) Если выбранные карточки не возвращаются, то события А₁, А₂, А₃ зависимы, и по теореме умножения для зависимых событий

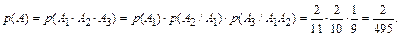
б) Если выбранные карточки возвращаются, то события А₁, А₂, А₃ не зависимы и по теореме умножения для независимых событий

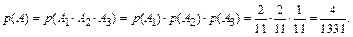
Ответ: а) 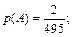б)