Асимптоты графика функции. а)Прямая х = а является вертикальной асимптотой графика функции у(х)
а)Прямая х = а является вертикальной асимптотой графика функции у(х), если хотя бы один из односторонних пределов: 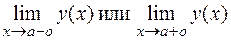 обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятся к точкам разрыва 2-го рода.
обращается в бесконечность. Поэтому для отыскания вертикальных асимптот графика функции надо найти точки бесконечного разрыва данной функции, которые относятся к точкам разрыва 2-го рода.
ПРИМЕР 34.Найти вертикальные асимптоты графика функции 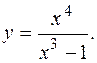
РЕШЕНИЕ:Как отмечалось, данная функция не определена в точке 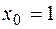 . При этом
. При этом
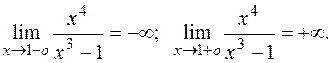
Поэтому прямая х = 1является вертикальной асимптотой графика заданной функции.
б) График функции у(х) имеет наклонную асимптоту у = kx + b при 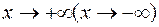 , если существуют конечные пределы:
, если существуют конечные пределы: 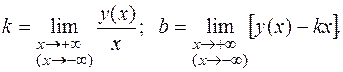 Если хотя бы один из этих пределов не существует или бесконечен, то график функции не имеет наклонной асимптоты при
Если хотя бы один из этих пределов не существует или бесконечен, то график функции не имеет наклонной асимптоты при 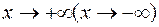 .(Если асимптота задана уравнением у = b, то ее называют горизонтальной).
.(Если асимптота задана уравнением у = b, то ее называют горизонтальной).
ПРИМЕР 35. Найти наклонные асимптоты графика функции 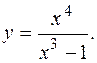
РЕШЕНИЕ: Найдем значения к и b для данной функции при 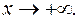
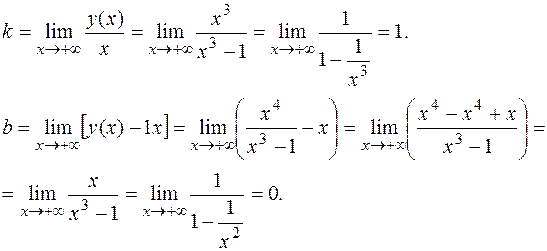
Аналогично находим, что при 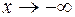 по-прежнему
по-прежнему 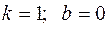 . Таким образом, график функции
. Таким образом, график функции 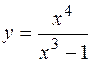 имеет одну и ту же наклонную асимптоту при
имеет одну и ту же наклонную асимптоту при 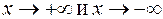 ; это прямая у = х.
; это прямая у = х.
Общий план исследования функции
Чтобы составить достаточно полное представление о характере поведения функции и построить ее график, удобно проводить ее исследование по следующему плану:
1. Установить множество определения функции; при наличии точек разрыва найти в них односторонние пределы данной функции;
2.а) Найти точки пересечения графика функции с осями координат,
б) Отметить особенности графика заданной функции, не связанные с производными, например, симметрию, периодичность.
3. Установить промежутки возрастания и убывания функции, найти ее экстремумы.
4. Установить промежутки выпуклости и вогнутости график функции, найти точки перегиба.
5 Найти асимптоты графика функции.
ПРИМЕР 36.Исследовать функцию 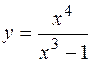 и сделать схематический чертеж ее графика.
и сделать схематический чертеж ее графика.
РЕШЕНИЕ:Как отмечалось в примере 32, множество определения данной функции - вся числовая ось Ох, исключая точку 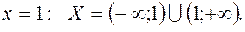 График функции пересекается с осями
График функции пересекается с осями 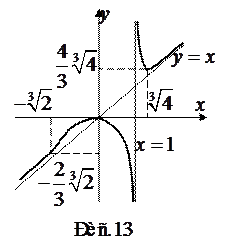 координат в единственной точке 0(0,0). Функция не является ни четной, ни нечетной, поскольку
координат в единственной точке 0(0,0). Функция не является ни четной, ни нечетной, поскольку 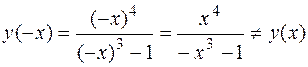 и
и 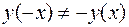 ,поэтому график функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 32 -35. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции, который представлен на рис.13.
,поэтому график функции не обладает свойствами симметрии. Дальнейшее исследование этой функции фактически уже проведено в примерах 32 -35. По данным, полученным в этих примерах, сделан схематический чертеж графика заданной функции, который представлен на рис.13.
ПРИМЕР 37.Исследовать функцию 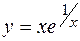 и сделать схематический чертеж ее графика.
и сделать схематический чертеж ее графика.
РЕШЕНИЕ:1. Множество определения данной функции - вся числовая ось Ох, кроме точки 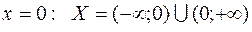 . Найдем односторонние пределы функции при
. Найдем односторонние пределы функции при 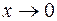 . Предел слева
. Предел слева 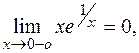 так как
так как 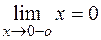 и
и 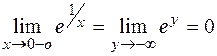 . При вычислении предела справа возникает неопределенность вида
. При вычислении предела справа возникает неопределенность вида 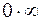 ; приводим ее к неопределенности вида
; приводим ее к неопределенности вида 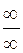 , к которой применяем правило Лопиталя:
, к которой применяем правило Лопиталя:
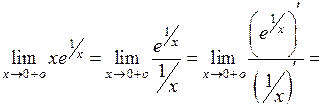
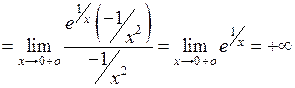
2. а) Точки пересечения графика функции с осью Ох определяются из условия у = 0. В данном случае уравнение 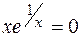 не имеет решений, так как х = 0 не входит в множество определения функции. Точки пересечения графика функции с осью Оу можно найти, положив х = 0. Для заданной функции это значение не входит в множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат.
не имеет решений, так как х = 0 не входит в множество определения функции. Точки пересечения графика функции с осью Оу можно найти, положив х = 0. Для заданной функции это значение не входит в множество ее определения. Следовательно, график исследуемой функции не имеет точек пересечения с осями координат.
б) Поскольку 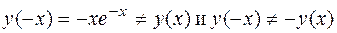 , то функция не является ни четной, ни нечетной.
, то функция не является ни четной, ни нечетной.
3. Находим
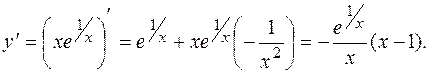
Производная у' существует и конечна на всем множестве определения заданной функции 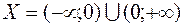 . Поскольку точка разрыва первой производной х = 0 не принадлежит множеству определения функции, то все критические точки функции
. Поскольку точка разрыва первой производной х = 0 не принадлежит множеству определения функции, то все критические точки функции 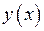 находим из условия:
находим из условия: 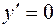 , или
, или 
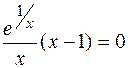 . Отсюда получаем
. Отсюда получаем 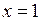 .
.
Функция 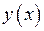 возрастает, если
возрастает, если 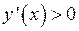 , то есть при
, то есть при 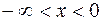 и
и 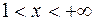 .
.
Функция 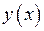 убывает, если
убывает, если 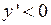 , в данном случае при
, в данном случае при 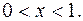 Таким образом, при переходе через точку
Таким образом, при переходе через точку 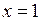 первая производная меняет знак с (-) на (+), то есть
первая производная меняет знак с (-) на (+), то есть 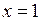 - точка минимума;
- точка минимума; 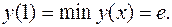
4. Находим 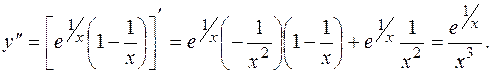
Вторая производная существует и конечна во всех точках множества определения данной функции. Тогда все точки перегиба находим из условия: у" = 0, то есть 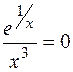 . Поскольку это уравнение не имеет решения, то точек перегиба нет. График функции - выпуклый, если у" < 0; в данном случае при х < 0. График функции вогнутый при x>0; > 0, где у" > 0.
. Поскольку это уравнение не имеет решения, то точек перегиба нет. График функции - выпуклый, если у" < 0; в данном случае при х < 0. График функции вогнутый при x>0; > 0, где у" > 0.
5. Как было установлено в пункте 1, в точке х = 0 функция 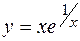 имеет бесконечный разрыв, поэтому прямая х = 0 является вертикальной асимптотой ее графика. Для определения наклонных асимптот найдем:
имеет бесконечный разрыв, поэтому прямая х = 0 является вертикальной асимптотой ее графика. Для определения наклонных асимптот найдем:
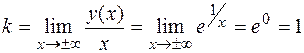

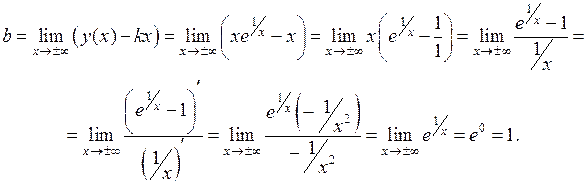
Значит, прямая у = x+1является наклонной асимптотой графика функции при 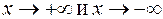 . Схематический чертеж графика функции приведен на рис.14.
. Схематический чертеж графика функции приведен на рис.14.
ПРИМЕР 38. Исследовать функцию 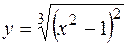 и сделать схематический чертеж графика.
и сделать схематический чертеж графика.
РЕШЕНИЕ:1). Данная функция определена на всей числовой
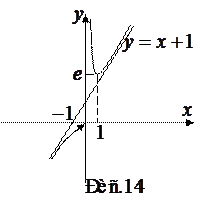 оси
оси 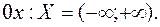
2). Точки пересечения графика функции с осью Ох определяются из условия 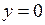 , откуда
, откуда 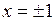 , а с осью
, а с осью 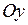 - из условия
- из условия 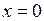 , при этом
, при этом 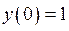 . Данная функция - четная, поскольку
. Данная функция - четная, поскольку 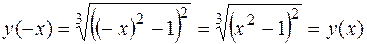 , значит, ее график симметричен относительно оси
, значит, ее график симметричен относительно оси 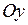 .
.
3). 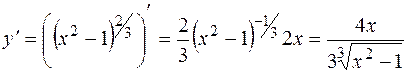 . Первая производная обращается в бесконечность в точках х = 1, х = -1, в то время, как сама функция
. Первая производная обращается в бесконечность в точках х = 1, х = -1, в то время, как сама функция 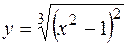 в этих точках определена. Значит, эти точки - критические для данной функции. Еще одна критическая точка определяется из условия у' = 0; это х = 0. Функция убывает, если у' < 0, то есть при
в этих точках определена. Значит, эти точки - критические для данной функции. Еще одна критическая точка определяется из условия у' = 0; это х = 0. Функция убывает, если у' < 0, то есть при 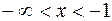 и
и 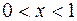 . Функция возрастает при у' > 0, то есть при -1 < х < 0 и при х > 1. Таким образом, х = 0 -точка максимума,
. Функция возрастает при у' > 0, то есть при -1 < х < 0 и при х > 1. Таким образом, х = 0 -точка максимума, 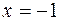 и
и 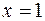 - точки минимума данной функции;
- точки минимума данной функции; 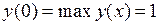 ;
; 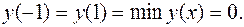 В точках х = -1 их = 1 данная функция имеет так называемый "острый" экстремум: касательная к графику функции в каждой из этих точек параллельна оси Оу.
В точках х = -1 их = 1 данная функция имеет так называемый "острый" экстремум: касательная к графику функции в каждой из этих точек параллельна оси Оу.
4). 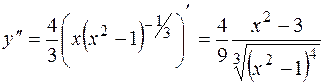 . Вторая производная обращается в бесконечность при х = ±1, но эти точки не принадлежат множеству определения у'(х)и, следовательно, не являются критическими точками для первой производной. Значит, критические точки для нее определяем из условия у" = 0, откуда
. Вторая производная обращается в бесконечность при х = ±1, но эти точки не принадлежат множеству определения у'(х)и, следовательно, не являются критическими точками для первой производной. Значит, критические точки для нее определяем из условия у" = 0, откуда 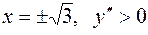 при
при 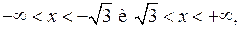 то график у(х)в этих интервалах вогнутый, а в интервалах
то график у(х)в этих интервалах вогнутый, а в интервалах 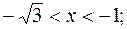
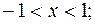
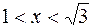 - график выпуклый, так как там у" < 0.
- график выпуклый, так как там у" < 0.
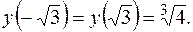
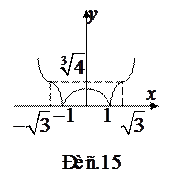 5). Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:
5). Поскольку функция определена на всей числовой оси Ox, то вертикальных асимптот у ее графика нет. Проверим наличие наклонных асимптот:
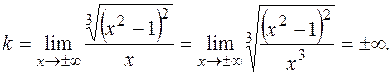
Таким образом, наклонные асимптоты также отсутствуют. На рис.15 схематически изображен график функции 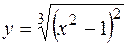 .
.
