Потенциальная энергия может быть определена исходя из (2.3) как

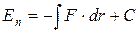(2.3)

где C – постоянная интегрирования.

Если тело перемещается вблизи поверхности Земли, то на него действует постоянная по величине и направлению сила тяжести 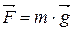. Работа этой силы зависит только от вертикального перемещения тела. На любом участке пути работу силы тяжести можно записать в проекциях вектора перемещения 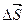на ось OY:

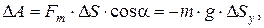
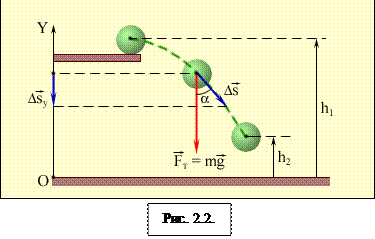
где 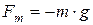– проекция силы тяжести, ΔS_y – проекция вектора перемещения. Если тело переместилось из точки, расположенной на высоте h₁, в точку, расположенную на высоте h₂ от начала координатной оси OY(рис. 2.2.), то сила тяжести совершила работу:

.

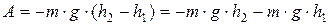Эта работа равна изменению некоторой физической величины 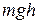, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести

E_p = mgh.

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

A = –(E_p2 – E_p1).

Найдём потенциальную энергию упругодеформированного тела (пружины). Сила упругости пропорциональна деформации:

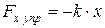
где F_{x упр}— проекция силы упругости на ось х,

k— коэффициент упругости (для пружины – жёсткость),

знак минус указывает, что F_{x упр} направлена в сторону, противоположную деформации х.

По третьему закону Ньютона, деформирующая сила равна по модулю силе упругости и противоположно ей направлена, т. е.

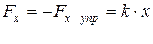
Элементарная работа dA, совершаемая силой F_xпри бесконечно малой деформации dx, равна:

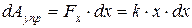
а полная работа

.

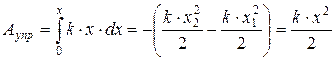идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела:

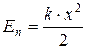
Полная механическая энергия системы:

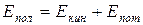
т.е. равна сумме кинетической и потенциальной энергий.

§ 3. Закон сохранения энергии

Рассмотрим систему материальных точек массами т₁, т₂... , т_n и движущихся со скоростями u₁, u₂..., u_n . Пусть F'₁, F'₂, ... , F'_n — равнодействующие внутренних консервативны сил, F₁, F₂ ..., F_n— равнодействующие внешних сил, а f₁, f₂ ..., f_n— равнодействующие внешних консервативных сил. Второй закон Ньютона для каждого из n тел механической системы:

, ,

………………

,

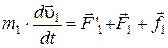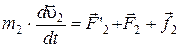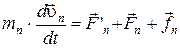Умножим каждое из уравнений на соответствующее перемещение и, учитывая, что 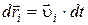, получим:

, ,

………………

,

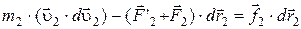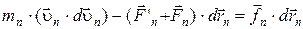Сложив эти уравнения, получим:

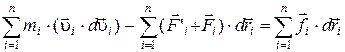(3.1)

.

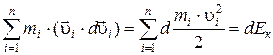где dЕ_к– кинетическая энергия системы.

Второй член 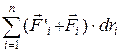равен элементарной работе внутренних и внешних консервативных сил, взятой со знаком минус, т. е. равен элементарному приращению потенциальной энергии dE_пот системы.

Правая часть равенства (3.1) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем

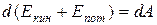(3.2)

При переходе системы из состояния 1 в какое-либо состояние 2:

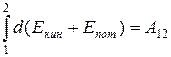
т. е. изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.2) следует, что:

,

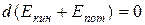откуда

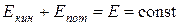,(3.3)

т. е. полная механическая энергия системы сохраняется постоянной. Выражение (3.3) представляет собой закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т. е. не изменяется со временем.

Пример применения закона сохранения энергии– нахождение минимальной прочности легкой нерастяжимой нити, удерживающей тело массой m при его вращении в вертикальной плоскости. Рис. 3.1 поясняет решение этой задачи.

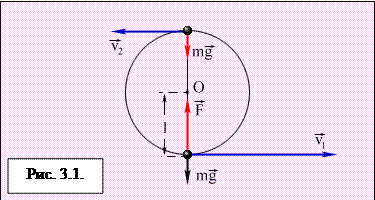Закон сохранения энергии для тела в верхней и нижней точках траектории записывается в виде:

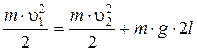
Обратим внимание на то, что сила 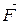натяжения нити всегда перпендикулярна скорости тела; поэтому она не совершает работы.

При минимальной скорости вращения натяжение нити в верхней точке равно нулю и, следовательно, центростремительное ускорение телу в верхней точке сообщается только силой тяжести:

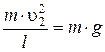
Из этих соотношений следует:

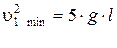
Центростремительное ускорение в нижней точке создается силам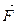и и 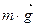направленными в противоположные стороны:

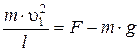
Отсюда следует, что при минимальной скорости тела в верхней точке натяжение нити в нижней точке будет по модулю равно:

.

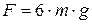Прочность нити должна, очевидно, превышать это значение.

МЕХАНИКА ТВЁРДОГО ТЕЛА

Момент инерции

Моментом инерции системы (твёрдого тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

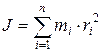
В качестве примера найдём момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси.

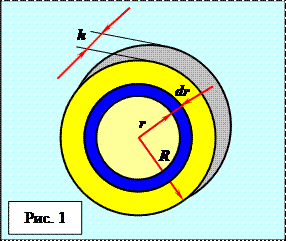
Разобьём цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+dr. Момент инерции каждого полого цилиндра:

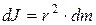
(т.к. dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r), где dm – масса всего элементарного цилиндра; его объём 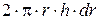. Если r – плотность материала, то 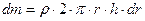или 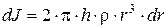. Тогда момент инерции сплошного цилиндра:

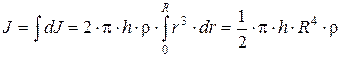
но т.к. 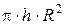– объём цилиндра, то его масса 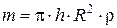, а момент инерции:

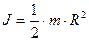
Теорема Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_C относительно параллельной оси, проходящей через центр масс C тела, сложенную с произведением массы m тела на квадрат расстояния a между осями:

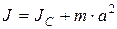
Значения моментов инерции некоторых тел приведены в табл. 1 (тепа считаются однородными, т — масса тепа).

Таблица 1

№ п.п.	Тело	Положения оси	Момент инерции
	Полый тонкостенный цилиндр радиусом R	Ось симметрии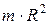
	Сплошной цилиндр или диск радиуса R	То же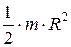
	Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходят через его середину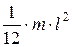
	Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец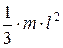
	Шар радиусом R	Ось проходят через центр шара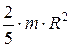
	Тонкостенная сфера радиусом R	Ось проходят через центр сферы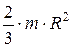