Непрерывные функции одной переменной
Функция y = f(x) называется непрерывной в точке x0, если она определена в некоторой окрестности точки x0 и 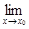 f(x) = f(x0).
f(x) = f(x0).
Это определение содержит следующие четыре условия непрерывности:
1) y = f(x) должна быть определена в некоторой окрестности точки x0;
2) должны существовать конечные пределы f(x0 + 0) = 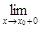 f(x) и f(x0 – 0) =
f(x) и f(x0 – 0) = 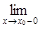 f(x) (пределы справа и слева − односторонние пределы);
f(x) (пределы справа и слева − односторонние пределы);
3) односторонние пределы должны быть одинаковыми;
4) эти пределы должны быть равны f(x0).
Если не выполняется хотя бы одно из условий 1–4, то функция имеет разрыв в точке x0.
Функция непрерывна в точке x0 справа, если выполняется условие
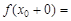
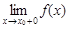 =
= 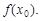
В противном случае функция имеет разрыв в точке 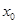 справа.
справа.
Функция непрерывна в точке 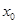 слева, если имеет место равенство
слева, если имеет место равенство
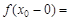
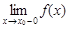 =
= 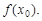
В противном случае функция имеет разрыв в точке 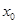 слева.
слева.
Из условий 2–4 следует, что если функция непрерывна в точке x0, то она непрерывна в этой же точке справа и слева.
Критерий непрерывности функции
Функция y = f(x) непрерывна в точке x0 тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
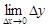 =
= 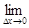
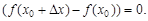
Пример 1.Доказать, что функция f(x) = x2 – 1 непрерывна в точке x = 4.
Доказательство. Найдем значение функции в точке x = 4, f(4) = 15.
Вычислим предел:
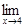
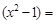
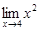 –
– 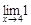 = 16 – 1 = 15.
= 16 – 1 = 15.
Получили, что предел функции в точке x = 4 равен значению функции в этой точке. Это означает, что условие непрерывности функции в точке выполнено, следовательно, данная функция непрерывна в точке x = 4.
Пример 2. Доказать, что функция f(x) = 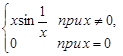 непрерывна в точке x = 0.
непрерывна в точке x = 0.
Доказательство. По условию f(0) = 0. Произведение x sin 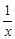 при
при
x ® 0 есть бесконечно малая величина как произведение бесконечно малой x на ограниченную величину sin 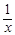
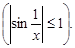 Предел бесконечно малой равен нулю, следовательно,
Предел бесконечно малой равен нулю, следовательно,
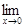
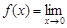
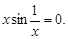
Получили, что 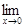
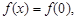 т. е. данная функция непрерывна в точке x = 0.
т. е. данная функция непрерывна в точке x = 0.
Пример 3. Доказать, что функция f(x)= 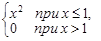 имеет разрыв в точке x = 1.
имеет разрыв в точке x = 1.
Доказательство. Значение функции в точке x = 1 есть f(1) = 1.
Найдем односторонние пределы функции в точке x = 1:
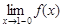 =
= 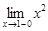
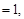
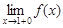 =
= 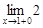
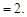
Получили, что в точке x = 1 предел слева не равен пределу справа, т. е. в этой точке предела не существует и функция при x = 1 имеет разрыв (рисунок 27).

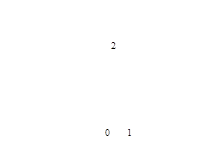
Рисунок 27
Тест 1. Функция f(x)= 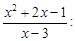
1) имеет одну точку разрыва;
2) имеет две точки разрыва;
3) является непрерывной.
Тест 2. Функция f(x)= 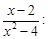
1) имеет одну точку разрыва;
2) имеет две точки разрыва;
3) является непрерывной.
Тест 3. Точкой разрыва функции f(x)= 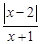 является:
является:
1) 1;
2) 2;
3) –1;
4) –2.
Тест 4.Точками разрыва функции f(x)= 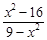 являются:
являются:
1) 4, 3;
2) 16, 9;
3) 4, –4;
4) 3, –3.
Тест 5. Точкой разрыва функции f(x) = 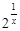 является:
является:
1) 1;
2) 2;
3) 0;
4) нет точек разрыва.
Тест 6. Точкой разрыва функции f(x)= 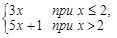 является:
является:
1) 5;
2) 2;
3) 3;
4) нет точек разрыва.
