Решение систем линейных уравнений методом Гаусса
Решить систему линейных уравнений общего вида с числом уравнений m меньшим или равным числу неизвестных n 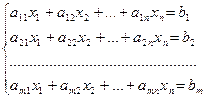 значит ответить на вопросы: имеет ли решение система или нет, то есть, является совместной или несовместной; если совместна, то является ли определенной , то есть имеет единственное решение, или не определенной – имеет множество решений.
значит ответить на вопросы: имеет ли решение система или нет, то есть, является совместной или несовместной; если совместна, то является ли определенной , то есть имеет единственное решение, или не определенной – имеет множество решений.
Метод Гаусса помимо возможности исследовать позволяет, в случае совместной системы, одновременно получить ее решение. Другое название метода Гаусса, точно выражающее его суть, - метод последовательного исключения неизвестных. Основная идея метода: из 1-го уравнения выразить 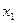 через остальные
через остальные 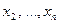 неизвестные и, подставляя выражение для
неизвестные и, подставляя выражение для 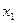 в каждое из последующих уравнений, исключить из этих уравнений вначале
в каждое из последующих уравнений, исключить из этих уравнений вначале 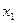 . Затем из полученного второго уравнения с исключенным
. Затем из полученного второго уравнения с исключенным 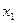 выразить
выразить 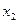 через остальные
через остальные 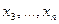 неизвестные, подставить это выражение для
неизвестные, подставить это выражение для 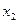 в каждое из последующих m-2 уравнений и таким образом из этих уравнений уже помимо
в каждое из последующих m-2 уравнений и таким образом из этих уравнений уже помимо 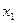 и исключить и
и исключить и 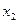 . Процесс исключения неизвестных можно продолжить и получить в конечном результате либо одно уравнение с одним неизвестным (определенная система), либо одно уравнение с несколькими неизвестными (неопределенная система), либо уравнение с противоречащими левой и правой частями (несовместная система). Применение метода Гаусса состоит в преобразовании заданной системы в равносильные системы, удовлетворяющие одним и тем же значениям неизвестных.
. Процесс исключения неизвестных можно продолжить и получить в конечном результате либо одно уравнение с одним неизвестным (определенная система), либо одно уравнение с несколькими неизвестными (неопределенная система), либо уравнение с противоречащими левой и правой частями (несовместная система). Применение метода Гаусса состоит в преобразовании заданной системы в равносильные системы, удовлетворяющие одним и тем же значениям неизвестных.
Преобразования системы выполняются действиями:
1) умножением любого из уравнений на любое действительное число;
2) алгебраическим сложением любых двух уравнений, умножением на любые действительные числа;
3) перестановкой уравнений своими местами;
4) исключением из системы уравнения, приведенного к виду равенства нулевых левой и правой частей: 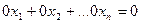 .
.
Решить систему методом Гаусса:
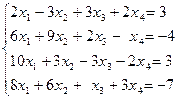
На примере заданной системы, содержащей 4 уравнения с 4-мя неизвестными, основную идею метода Гаусса возможно осуществить следующим образом:
1) разделить каждое уравнение на коэффициент при 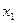 , чтобы приравнять коэффициенты при
, чтобы приравнять коэффициенты при 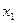 :
:
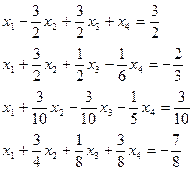
2) из второго, третьего и четвертого уравнений вычесть первое уравнение, чтобы из 2-го, 3-го и 4-го уравнений исключить 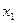 :
:
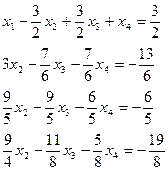
3) разделить второе, третье и четвертое уравнения на коэффициент при 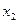 :
:
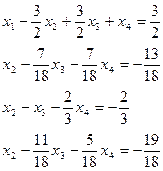
4) из третьего и четвертого уравнений вычесть второе уравнение, чтобы из 3-го и 4-го уравнений исключить 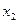 :
:
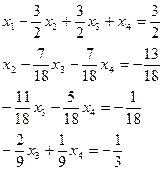
5) разделить 3-е и 4-е уравнения на коэффициент при 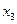 , чтобы приравнять коэффициенты при
, чтобы приравнять коэффициенты при 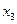 :
:
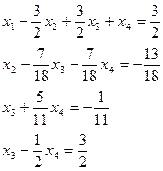
6) из четвертого уравнения вычесть третье уравнение, чтобы из 4-го уравнения исключить 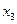 :
:
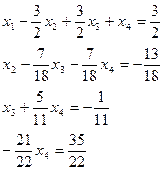
Путем равносильных преобразований, последовательно исключая неизвестные, заданную систему привести к виду, содержащему одно уравнение с одним неизвестным. Такая система является совместной и определенной. Чтобы получить решение, из 4-го уравнения находим 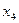 и , в обратном порядке, из 3-го уравнения получим
и , в обратном порядке, из 3-го уравнения получим 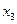 , из второго -
, из второго - 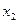 , а из первого -
, а из первого - 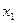 :
:
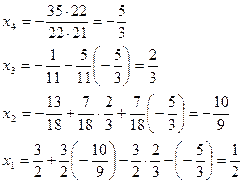
Проверка:
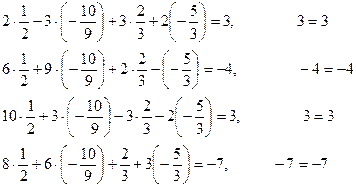
Ответ:
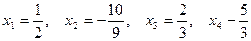 .
.
