Условия несовместности СЛАУ
Определение. Для системы линейных уравнений матрица
А*= 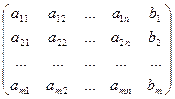
называется расширенной матрицей системы.
Следующая теорема Кронекера-Капелли (Леопольд Кронекер (1823-1891), немецкий математик) устанавливает условие совместности СЛАУ.
Теорема (Кронекера-Капелли).Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы:
RgA = RgA*.
Доказательство.Очевидно, что система может быть записана в виде:
x1 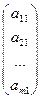 + x2
+ x2 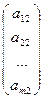 + … + xn
+ … + xn 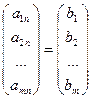 .
.
1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А* не изменяют ранга.
2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.
Пример 1. Определить совместность системы линейных уравнений:
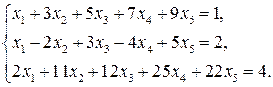
Решение.Приводим расширенную матрицу системы к ступенчатому виду, чтобы определить ранг матриц.
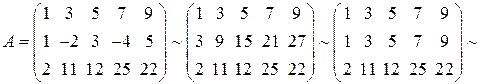
~ 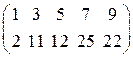 .
.
Базисный минор 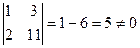 , RgA = 2.
, RgA = 2.
A* = 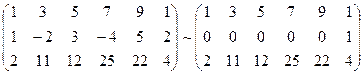 , RgA* = 3.
, RgA* = 3.
Система несовместна.
Пример 2. Определить совместность системы линейных уравнений.
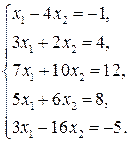
Решение. А = 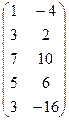 ;
; 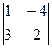 = 2 + 12 = 14 ¹ 0; RgA = 2;
= 2 + 12 = 14 ¹ 0; RgA = 2;
A* = 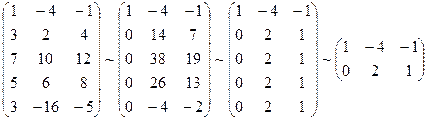
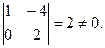 RgA* = 2.
RgA* = 2.
Система совместна.
Пример 3. Решить систему линейных уравнений методом Гаусса.
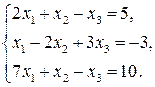
Решение.Составим расширенную матрицу системы.
А* = 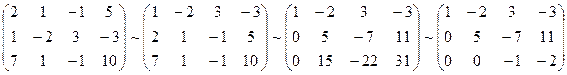 .
.
Таким образом, исходная система может быть представлена в виде:
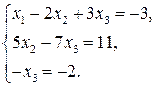 ,
,
откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Метод исключения переменных Гаусса для решения СЛАУ.
Условия существования множества решений СЛАУ
(нахождение общего решения СЛАУ)
Лекция 10
Однородные системы линейных алгебраических уравнений, свойства решений.
Понятие фундаментальной системы (ФСР) решений ОСЛАУ. Структура общего решения неоднородной СЛАУ.
Однородные системы линейных алгебраических уравнений,
Свойства решений
Определение 1. Если в каждом уравнении СЛАУ свободные члены равны нулю, то эта система называется однородной.
Однородную систему можно записать в следующем виде:
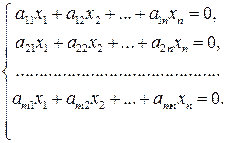 (15.1)
(15.1)
Рассмотрим основные свойства однородных систем.
Теорема 1. Однородная система (15.1) всегда совместна (она имеет, по крайней мере, одно решение – нулевое).
Доказательство теоремы очевидно.
Возникает вопрос: в каком случае система (15.1) будет иметь и ненулевые решения? Ответ на этот вопрос даёт следующая теорема.
Теорема 2.Для того чтобы система (15.1) имела ненулевые решения, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа переменных 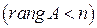 .
.
Доказательство.
1. Необходимость.Пусть система имеет ненулевые решения, ранг матрицы системы, по определению, не может быть больше числа переменных, следовательно, 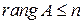 . Пусть
. Пусть 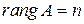 , тогда из общей теории систем следует, что система имеет единственное решение, т.е. нулевое. Значит,
, тогда из общей теории систем следует, что система имеет единственное решение, т.е. нулевое. Значит, 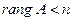 .
.
2. Достаточность.Пусть 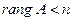 , тогда из общей теории СЛАУ следует, что система (41) имеет бесчисленное множество решений, одно из них нулевое, а остальные – ненулевые.
, тогда из общей теории СЛАУ следует, что система (41) имеет бесчисленное множество решений, одно из них нулевое, а остальные – ненулевые.
Следствие 1.Если число уравнений в системе (15.1) меньше числа переменных, то система (15.1) имеет ненулевые решения.
Доказательство.Так как 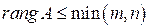 , а
, а 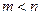 , то
, то 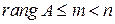 , тогда по теореме система имеет ненулевые решения.
, тогда по теореме система имеет ненулевые решения.
Следствие 2.Пусть основная матрица системы (15.1) квадратная 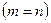 . В этом случае, для того чтобы система (15.1) имела ненулевые решения, необходимо и достаточно, чтобы определитель основной матрицы системы был равен нулю.
. В этом случае, для того чтобы система (15.1) имела ненулевые решения, необходимо и достаточно, чтобы определитель основной матрицы системы был равен нулю.
Доказательство.
1. Необходимость.Пусть система (15.1) имеет ненулевые решения, тогда по теореме 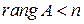 , следовательно,
, следовательно, 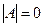 .
.
2. Достаточность.Пусть 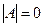 , следовательно,
, следовательно, 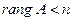 , тогда по теореме система имеет ненулевые решения.
, тогда по теореме система имеет ненулевые решения.
Теорема 3.Если 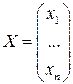 – решение системы (15.1), то
– решение системы (15.1), то 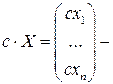 также решение (15.1).
также решение (15.1).
Доказательство.Так как 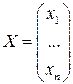 - решение
- решение 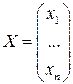 , то
, то 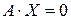 .
. 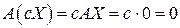 , значит,
, значит, 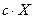 – решение (1.41).
– решение (1.41).
Теорема 4.Если 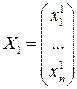 ,
, 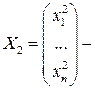 решения (15.1), то
решения (15.1), то 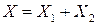 – решение (15.1).
– решение (15.1).
Доказательство.Так как 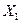 ,
, 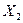 – решения (1.41), то
– решения (1.41), то 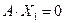 ,
, 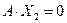 , тогда
, тогда
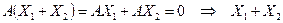 – решение (1.41).
– решение (1.41).
