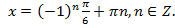Теоретические сведения и примеры. Рассмотрим множество натуральных чисел N
Рассмотрим множество натуральных чисел N. Каждому натуральному числу по определенному правилу поставим в соответствие некоторое другое число. Получим бесконечную числовую последовательность, которую можно считать функцией, заданной на множестве натуральных чисел. Числовую последовательность принято обозначать 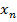 или аn, где
или аn, где 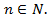 Последовательность чаще всего задается формулой n-го члена или дается правило, по которому, зная предыдущие члены, можно вычислить последующие (рекуррентное задание последовательности).
Последовательность чаще всего задается формулой n-го члена или дается правило, по которому, зная предыдущие члены, можно вычислить последующие (рекуррентное задание последовательности).
Например, последовательность чисел 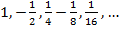
может быть задана формулой 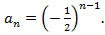
Действительно, если 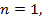 то
то 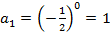 , если
, если 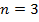 , то
, то 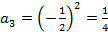 и т. д.
и т. д.
Числовая последовательность может быть конечной, если в ней содержится ограниченное количество чисел, т. е. сопоставление проводится не для всех натуральных чисел, а только для некоторых из них.
Если каждый член последовательности, начиная со второго, больше предыдущего, то последовательность называется монотонно возрастающей. Если каждый член последовательности, начиная со второго, меньше предыдущего, то последовательность называется монотонно убывающей. Монотонно возрастающие и монотонно убывающие последовательности иногда называются просто монотонными.
Особый интерес для нас представляют последовательности, называемые арифметической и геометрической прогрессиями.
Числовая последовательность называется арифметической прогрессией, если каждый ее член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, т. е. арифметическая прогрессия задается рекуррентно следующим образом: 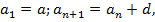 где
где 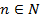 (число d называется разностью прогрессии). Зная первый член прогрессии, а также ее разность, можно вычислить значение любого другого члена прогрессии:
(число d называется разностью прогрессии). Зная первый член прогрессии, а также ее разность, можно вычислить значение любого другого члена прогрессии: 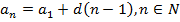 .
.
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов, т. е. 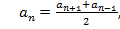 где
где 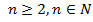 характеристическое свойство арифметической прогрессии.
характеристическое свойство арифметической прогрессии.
Формула суммы первых n членов прогрессии:
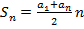 или
или 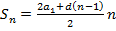 ,
, 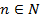 .
.
Если разность арифметической прогрессии – положительное число, то такая прогрессия называется возрастающей; если разностью является отрицательное число, то прогрессия называется убывающей.
Из определения разности арифметической прогрессии
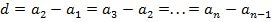 следует, что
следует, что 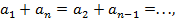 т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
т. е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.
Числовая последовательность называется геометрической прогрессией, если первый ее член отличен от нуля, а каждый последующий равен предыдущему, умноженному на некоторое постоянное для данной последовательности число, отличное от нуля. Геометрическая прогрессия задается рекуррентно следующим образом: 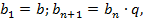 где
где 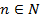 (число q называется знаменателем прогрессии).
(число q называется знаменателем прогрессии).
Для того чтобы задать геометрическую прогрессию, достаточно знать ее первый член и знаменатель, тогда всякий член прогрессии может быть вычислен по формуле 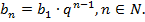
Из определения геометрической прогрессии следует, что отношение любого ее члена к предшествующему равно одному и тому же числу, т. е. 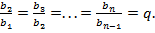
Если 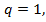 то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. Если
то все члены прогрессии равны между собой. В этом случае прогрессия является постоянной последовательностью. Если 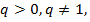 то прогрессия является монотонной последовательностью, а именно возрастающей, если
то прогрессия является монотонной последовательностью, а именно возрастающей, если 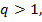 и убывающей, если
и убывающей, если 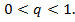 Если
Если 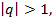 то прогрессия называется возрастающей по абсолютной величине, если же
то прогрессия называется возрастающей по абсолютной величине, если же 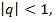 то прогрессия называется убывающей по модулю. В случае, когда число членов убывающей прогрессии бесконечно, прогрессия называется бесконечно убывающей.
то прогрессия называется убывающей по модулю. В случае, когда число членов убывающей прогрессии бесконечно, прогрессия называется бесконечно убывающей.
Прогрессия называется геометрической тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему геометрическому соседних с ним членов, т. е. 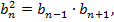 где
где 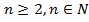 (характеристическое свойство геометрической прогрессии).
(характеристическое свойство геометрической прогрессии).
Формула суммы первых n членов прогрессии 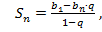 или
или 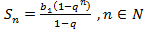 (в случае
(в случае 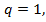
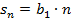 ).
).
Если геометрическая прогрессия, бесконечно убывающая 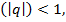 то ее сумма вычисляется по формуле
то ее сумма вычисляется по формуле 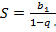
Задача 1.Сумма трех положительных членов арифметической прогрессии равна 21. Если к этим числам прибавить 2; 3 и 9 соответственно, то новые числа образуют геометрическую прогрессию. Найти эти числа.
Решение. Пусть 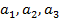 – первые члены арифметической прогрессии и их сумма равна 21, т. е.
– первые члены арифметической прогрессии и их сумма равна 21, т. е. 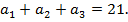 Так как прогрессия арифметическая, то
Так как прогрессия арифметическая, то 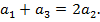
По условию задачи числа 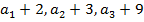 образуют геометрическую прогрессию, т.е
образуют геометрическую прогрессию, т.е 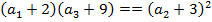 .
.
Получим систему уравнений и решим ее:
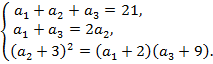
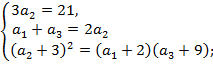
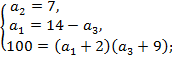
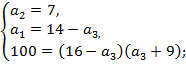
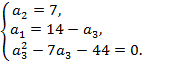
Уравнение 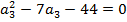 имеет один целый положительный корень
имеет один целый положительный корень 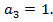
Отсюда 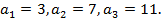 Значит, числа 5; 10; 20 образуют геометрическую прогрессию.
Значит, числа 5; 10; 20 образуют геометрическую прогрессию.
Ответ: искомые числа 5; 10; 20.
Задача 2. Найти сумму первых четырех членов геометрической прогрессии, обладающей тем свойством, что ее первые три члена, сумма которых равна 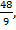 являются одновременно первым, четвертым и восьмым членами некоторой арифметической прогрессии.
являются одновременно первым, четвертым и восьмым членами некоторой арифметической прогрессии.
Решение. Пусть числа 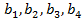 образуют геометрическую прогрессию, причем
образуют геометрическую прогрессию, причем 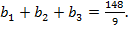 Так как
Так как 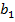 является одновременно первым,
является одновременно первым, 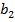 – четвертым членами некоторой арифметической прогрессии, то
– четвертым членами некоторой арифметической прогрессии, то 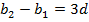 , где d – разность этой арифметической прогрессии. Но
, где d – разность этой арифметической прогрессии. Но 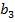 является также восьмым членом этой же прогрессии, поэтому
является также восьмым членом этой же прогрессии, поэтому 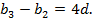 Данные условия можно записать в виде системы уравнений
Данные условия можно записать в виде системы уравнений 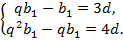
Разделив второе уравнение на первое, получим 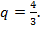 Но
Но 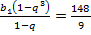 отсюда
отсюда 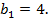 Найдем сумму первых четырех членов геометрической прогрессии по формуле:
Найдем сумму первых четырех членов геометрической прогрессии по формуле:
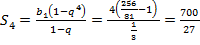
Ответ: сумма первых четырех членов 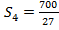
Задача 3. В трех растворах проценты содержания спирта образуют геометрическую прогрессию. Если смешать первый, второй и третий растворы в весовом отношении 2:3:4, то получится раствор, содержащий 32 % спирта. Если же смешать их в весовом отношении 3:2:1, то получится раствор, содержащий 22 % спирта. Каков процент спирта в каждом растворе?
Решение. Пусть х – концентрация спирта в первом растворе. Так как проценты содержания спирта в трех растворах образуют геометрическую прогрессию, то 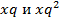 – концентрации спирта во втором и третьем растворах соответственно (q – некоторое постоянное число). Если взять две части первого раствора, три части второго и четыре части третьего, то получится 9 частей 32%-го раствора спирта, т. е.
– концентрации спирта во втором и третьем растворах соответственно (q – некоторое постоянное число). Если взять две части первого раствора, три части второго и четыре части третьего, то получится 9 частей 32%-го раствора спирта, т. е. 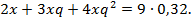 Для второго случая уравнение имеет вид
Для второго случая уравнение имеет вид 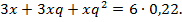
Решим систему уравнений:
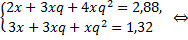
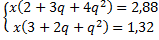
Исключим х из уравнений: 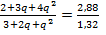 или
или 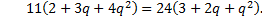
Получим уравнение 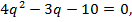 которое имеет один положительный корень
которое имеет один положительный корень 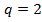 . При
. При 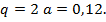 Значит, растворы содержат 12; 24 и 48 % спирта соответственно.
Значит, растворы содержат 12; 24 и 48 % спирта соответственно.
Ответ: первый раствор содержит 12 % спирта, второй – 24 %, третий – 48 %.
Задача 4.
Решить уравнение 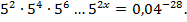
Решение. Перепишем уравнение в виде 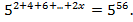 Отсюда
Отсюда 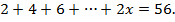
Левая часть уравнения представляет собой арифметическую прогрессию, первый член которой равен 2 и разность равна 2. Число членов прогрессии равно х.
Найдем сумму этой прогрессии.
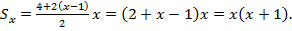
Из предыдущего равенства 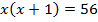 .
.
Полученное уравнение 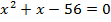 имеет один положительный корень
имеет один положительный корень 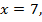 который является решением исходного уравнения.
который является решением исходного уравнения.
Ответ: 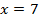 .
.
Задача 5. Решить уравнение :
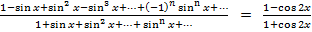
Решение. Допустимые значения неизвестного удовлетворяют условию
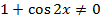 или
или 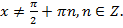
В числителе и знаменателе дроби – геометрические бесконечно убывающие прогрессии, суммы которых равны, согласно формуле, соответственно 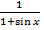 и
и 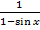 .
.
Исходное уравнение примет вид
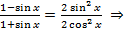
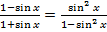 ⇒
⇒
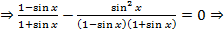
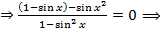
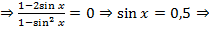
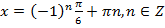
Ответ: