Общее уравнение плоскости в пространстве
Пусть в пространстве 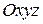 плоскость задана точкой
плоскость задана точкой 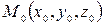 , лежащей в этой плоскости и вектором
, лежащей в этой плоскости и вектором 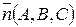 , перпендикулярным этой плоскости (в дальнейщем такого рода векторы будем называть векторами нормали). Выведем уравнение плоскости. Очевидно, что точка
, перпендикулярным этой плоскости (в дальнейщем такого рода векторы будем называть векторами нормали). Выведем уравнение плоскости. Очевидно, что точка 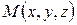 лежит в данной плоскости тогда и только тогда, когда вектор
лежит в данной плоскости тогда и только тогда, когда вектор
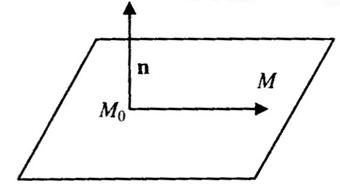
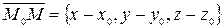
будет перпендикулярен заданному вектору нормали 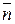 . Это равносильно тому, что скалярное произведение этих векторов равно нулю:
. Это равносильно тому, что скалярное произведение этих векторов равно нулю:
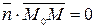
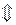
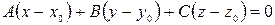 .
.
Последнее равенство и является уравнением плоскости, проходящей через заданную точку перпендикулярно заданному вектору.
Если раскрыть скобки в последнем уравнении, то получим линейное уравнение первого порядка:
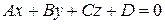 ,
,
где
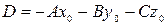 .
.
Покажем обратное, т.е. что любое такое уравнение при условии 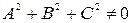 является уравнением некоторой плоскости. Условие
является уравнением некоторой плоскости. Условие 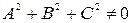 означает, что хотя бы один из коэффициентов
означает, что хотя бы один из коэффициентов 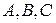 отличен от нуля. Пусть это будет, например, коэффициент
отличен от нуля. Пусть это будет, например, коэффициент 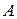 . Перепишем тогда рассматриваемое уравнение в виде:
. Перепишем тогда рассматриваемое уравнение в виде:
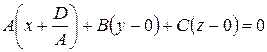 .
.
Получилось уравнение плоскости, проходящей через точку 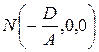 , и имеющей вектор нормали
, и имеющей вектор нормали 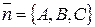 . Таким образом, уравнение
. Таким образом, уравнение 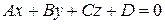 является уравнением плоскости и называется ее общим уравнением.
является уравнением плоскости и называется ее общим уравнением.
Угол 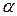 между плоскостями
между плоскостями
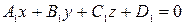
и
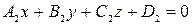
может быть найден как угол между их векторами нормали 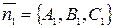 и
и 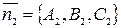 , т.е. по формуле:
, т.е. по формуле:
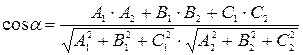 .
.
В частности, указанные плоскости будут параллельны, если векторы 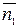 и
и 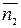 коллинеарны, т.е. при условии:
коллинеарны, т.е. при условии:
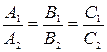 .
.
Эти же плоскости будут перпендикулярны, если векторы 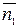 и
и 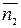 ортогональны, т.е. при условии:
ортогональны, т.е. при условии:
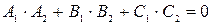 .
.
Общее уравнение плоскости называется полным, если все его коэффициенты не равны нулю. Если хотя бы один из коэффициентов общего уравнения равен нулю, то это уравнение называется неполным. Рассмотрим все возможные виды неполных уравнений.
1) Пусть 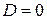 . Тогда получаем уравнение
. Тогда получаем уравнение
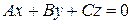 ,
,
которое определяет плоскость, проходящую через начало координат.
2) Пусть 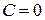 . Тогда получаем уравнение
. Тогда получаем уравнение
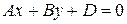 .
.
Тогда вектор нормали 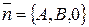 этой плоскости перпендикулярен оси
этой плоскости перпендикулярен оси 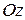 . Следовательно, такая плоскость параллельна этой оси.
. Следовательно, такая плоскость параллельна этой оси.
Аналогично в случае 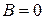 получаем плоскость параллельную оси
получаем плоскость параллельную оси 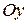 , а в случае
, а в случае 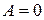 - плоскость, параллельную оси
- плоскость, параллельную оси 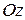 .
.
3) Пусть 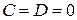 . Тогда получаем уравнение
. Тогда получаем уравнение
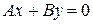
или
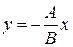 .
.
Такое уравнение определяет плоскость, проходящую через ось 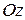 .
.
Аналогично плоскость
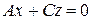
или
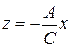
проходит через ось 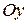 .
.
Плоскость
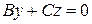
или
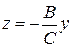
проходит через ось 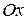 .
.
4) Пусть 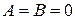 . Тогда получаем уравнение
. Тогда получаем уравнение
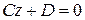
или
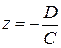 .
.
Такая плоскость параллельна координатной плоскости 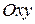 .
.
Аналогично плоскость
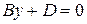
или
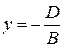 .
.
параллельна координатной плоскости 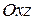 .
.
Плоскость
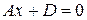
или
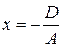
параллельна координатной плоскости 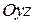 .
.
5) Пусть 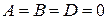 . Тогда получаем уравнение
. Тогда получаем уравнение
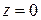 .
.
Это уравнение плоскости 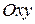 .
.
Аналогично в случае 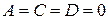 получаем уравнение плоскости
получаем уравнение плоскости 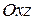 :
:
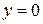 ,
,
а в случае 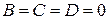 получаем уравнение плоскости
получаем уравнение плоскости 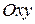 .
.
Пример.Найти двугранный угол между плоскостями
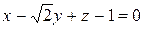
и
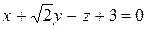 .
.
∆ Искомый угол 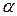 найдем по формуле:
найдем по формуле:
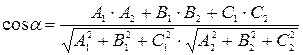 .
.
В результате получаем:
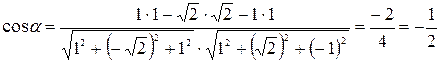 .
.
Следовательно, угол между плоскостями равен 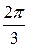 . Очевидно, что между данными плоскостями есть также острый угол, равный
. Очевидно, что между данными плоскостями есть также острый угол, равный 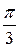 . ▲
. ▲
